Существует несколько видов модулей-оригами из бумаги, но треугольники пользуются наибольшей популярностью. Только они позволяют создавать самые разнообразные модели на базе одной и той же «строительной» единицы. Фантазия оригамистов ничем не ограничена – из миниатюрных треугольников можно складывать цветы, животных, вазы и архитектурные объекты, размером от человеческой ладони до двух метров и более.
- Что такое треугольный модуль
- Модуль-треугольник
- Три модели в технике модульного оригами
- Китайский мини-дракон
- Лебедь
- Историческая справка
- Какие ещё бывают треугольники-оригами
- «Двойной треугольник»
- Солдатское письмо
- Пирамида из бумаги своими руками. Схемы и способы изготовления
- Как сделать объемные геометрические фигуры
- Из бумаги
- Из картона
- Развертки куба
- Треугольника
- Прямоугольника
- Цилиндра
- Ромба
- Призмы
- Задание 2 (построение прямоугольного треугольника)
- Схемы для вырезания
- Конуса
- Пирамиды
- Шестигранника
- Макета с припусками
- Параллелепипеда
- Трапеции
- Овала
- Многогранника
- Параллелограмма
- Задание 1 (определение вида треугольников)
- Шаблоны для склеивания
- Сложных фигур
- Октаэдра
- Тетраэдра
- Икосаэдра
- Додекаэдра
- Гексаэдра
- Фигурок из треугольников
- Виды углов
- Макеты из бумаги
- Оригами
- Животные
- Корабль
- Полигональные чертежи
- Игрушки из фигур
- Геометрические маски
- Карандаш
- Многогранники. Виды многогранников и их свойства
- Понятие многогранника, виды многогранников в геометрии
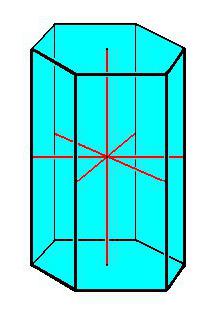
- Призма и её свойства
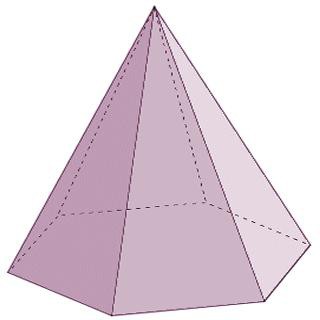
- Пирамида
- Правильный многогранник: виды и свойства многогранников
- Гексаэдр и его свойства
- Тетраэдр
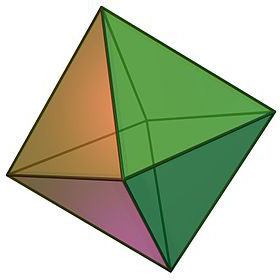
- Октаэдр и его свойства
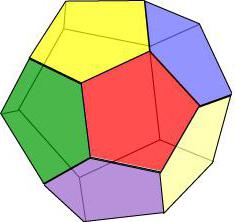
- Додекаэдр
- Икосаэдр
- Полуправильные многоугольники
- Звёздчатые многогранники
Видео:Икосаэдр из бумаги. Чертёж развертки икосаэдра.Скачать

Что такое треугольный модуль
В основе элемента лежит прямоугольник, размером от 1/4 до 1/36 альбомного листа (формат А4). Соединяются готовые модули за счёт выступающих «уголков» и глубоких «карманчиков», по принципу штекерного разъёма. Плотное прилегание деталей обеспечивает прочность конструкции, но для большей надёжности лучше дополнительно «посадить» их на клей.
Перед тем как делать треугольники для модульного оригами, необходимо нарезать прямоугольные заготовки определённого размера. Допустимо одновременное использование нескольких «калибров»: более крупного для основных объёмов и мелкого – для изящного декора. Разделить лист на модули можно, опираясь на базовую форму «Дверцы». Для самого ходового элемента 1/16 потребуется:
- Сложить лист пополам в продольном направлении.
- Раскрыть.
- Каждую половинку сложить к центральной линии.
- Раскрыть заготовку и повторить те же действия в поперечном направлении. В результате лист будет поделен на 16 частей, размером 7,4х5,3 см.
Получить 1/32 несколько сложнее. Лист А4 сначала в поперечном направлении делят вдоль центральной оси, а затем каждую половину складывают в четыре раза. Получается вдвое больше полос, чем в предыдущем случае. Для продольного направления действия те же, что и при разметке модуля 1/16. В результате образуются прямоугольники, размером 5,3х3,7 см. Нарезать заготовки лучше всего канцелярским ножом, подложив под лист доску, ДВП или специальный макетный коврик.
Получить прямоугольники 1/32 можно и другим способом:
Модуль-треугольник
Сложить из прямоугольной заготовки треугольную деталь не составит никакого труда. Единственное «но» – таких элементов потребуется очень много, в среднем, на одну фигурку высотой 25 – 30 см около 1000 штук. Опытные мастера советуют по мере возможности пополнять запасы деталей, занимаясь другими делами. Например, во время просмотра любимого сериала или прогулки с ребёнком. После некоторой тренировки, складывать треугольники получается, даже не глядя.
Пошаговая инструкция:
- Располагаем исходный прямоугольник длинной стороной к себе.
- Складываем пополам сверху вниз (это важно, поскольку свободный край должен «смотреть» на нас). Заготовку сгибаем вдвое поперёк, чтобы обозначить у неё середину. Раскрываем.
- Правый и левый край опускаем вниз, выравнивая по центру. Переворачиваем.
- Подгибаем внешние уголки заготовки.
- Подворачиваем нижнюю часть до линии основания треугольника.
- Складываем фигуру пополам «долиной».
В итоге получаем классические треугольники для модульного оригами:
Существует несколько типов соединений модульных элементов. Они зависят:
- от выбора стороны, которой одна деталь соединяется с другой;
- от взаимного расположения «уголка» и «карманчика».
Азбука модульного дела:
- У треугольного модуля есть две коротких стороны, расположенных напротив углов в 60° и одна длинная – напротив прямого. На рисунке они обозначены соответственно, КСН и ДСН.
- Соединение на коротких сторонах (КСН).
- То же, но на длинных (ДСН).
- «Змейка», когда модульные элементы соединяются один в один.
- Классическое соединение «две длинных стороны и одна короткая».
- «Все короткие».
Видео:Оригами октахедрон • Геометрическая фигура окраэдр из 1 листа бумаги без клея • Oridami OctahedronСкачать

Три модели в технике модульного оригами
Начинающим мастерам не всегда знакомы тонкости «бумажного искусства». Главное при сборке оригами из модулей-треугольников, как и в других видах рукоделия: вышивке, плетении или вязании, не спешить и на каждом этапе чётко следовать схеме. Тогда работа сразу получится аккуратной и прочной, не требуя переделок. Есть и другие значимые моменты:
- Модули необходимо складывать очень точно, иначе изделие будет перекошенным и неряшливым. Чем меньше размер сборочных элементов, тем тоньше выбирают бумагу для них.
- Если «карманчики» трудно раскрываются, можно воспользоваться зубочисткой.
- Начинать знакомство с модульным оригами лучше с лёгких моделей, постепенно переходя к более сложным.
- Склеивание элементов изделия поможет сохранить его на длительный срок и убережёт от разрушения при падении.
- Готовые работы стоит покрыть прозрачным лаком для дерева. Это – хорошая защита от пыли и выцветания, а также возможность делать влажную уборку.
Удачная модель для тех, кто только начинает знакомиться с техникой складывания оригами из маленьких треугольников. Для неё понадобится всего 106 синих модулей и 24 розовых.
Схема «Совы»:
Сборка ведётся на длинных сторонах. 1-й ряд состоит из 16 синих элементов. Начиная со 2-го, добавляем розовые детали для «манишки» совы (12+4).
Общее число элементов в каждом ряду одинаковое. Но соотношение по цветам разное.
3-й ряд: 10 синих и 5 розовых деталей.
4-й ряд: 8 синих и 6 розовых.
Далее модули распределяются в обратной последовательности. Для предпоследнего ряда берём 16 синих деталей, для последнего – 15.
Собрав сову, делаем её характерные «ушки». Они состоят из 3-х деталей, которые крепятся на последний ряд, по тому же принципу, что и остальные. Затем приклеиваем птице глаза и нос из розового модульного элемента.
«Сова» яркого сказочного окраса украсит дом на Хэллоуин или другой тематический праздник. Также она будет эффектно смотреться в детской.
Китайский мини-дракон
Следуя принципу постепенного усложнения моделей, после сверх-простой совы как раз можно перейти к популярному на востоке символу водной стихии. Дракон в Китае издавна был связан с культом плодородия, без его изображений не обходился ни один ритуал вызывания дождя. Кроме того, этот мифический персонаж обозначал принадлежность к высшим слоям общества. Его изображениями разрешалось украшать одежду только аристократии, простолюдинам же, подобная «вольность» была недоступна.
Для того, чтобы сделать мини-дракона, понадобится 515 бумажных треугольников-оригами 1/16:
Голова
Начинаем работу с головы. Схема её сборки:
Двигаемся от «подбородка» вверх.
| Ряд | Количество модулей |
| 1 | 3 С |
| 2 | 4 С |
| 3 | 3 С |
| 4 | 4 С |
| 5 | 5 С |
| 6 | 4 С |
| 7 | 1 С+1 Ж+1 С+1 Ж+1 С |
| 8 | 6 С |
| 9 | 5 С |
| 10 | 6 С |
Сборку производим сверху вниз. Завершив 10 ряд, делаем шипы, венчающие драконью голову. Собираем их симметрично по схеме, сделав пропуск посредине. Переворачиваем фигуру и слегка изгибаем – голова почти готова. Из красной бумаги вырезаем раздвоенный язык и приклеиваем по центру последнего ряда с изнанки.
Туловище дракона
Гибкое тело мифического животного представляет собой цепочку из жёлтых и синих деталей. Вначале их три: С+Ж+С. К первой жёлтой детали в следующем ряду добавляем ещё две, надевая на каждый уголок.
Затем вновь повторяем начальное расположение треугольников и так продолжаем, пока не наберём примерно 88 рядов. Для тела потребуется 176 синих и 262 жёлтых элемента. Закончив сборку, к голове с обратной стороны в районе глаз добавляют два синих крепёжных модуля.
Изготавливаем 4 лапки из 5 синих деталей. Присоединяем заготовки к туловищу в точках опоры. Предварительно изгибаем его, наподобие американских горок.
Лебедь
Это одна из самых красивых и востребованных моделей. Лебедь-оригами из модульных треугольников легко превращается в элегантную вазу для сухоцветов, хотя и сам по себе он великолепен.
Для двухцветной модели, представленной в следующем видео-уроке, понадобится 1522 модуля, размером 1/32:
Видео:Икосаэдр из бумаги/Paper icosahedron/Правильный многогранник/DIYСкачать

Историческая справка
Под модульным оригами чаще всего подразумевают именно фигуры из маленьких треугольников. Однако существуют ещё шары-кусудамы и многогранники из так называемых «модулей Сонобе.» Обе разновидности родом из Японии. Кусудама – бумажный шар из нескольких сшитых или склеенных между собой секций, известна со времён Средневековья. Её наполняли ароматными травами, выделявшими целебные эфирные масла, и развешивали в доме для защиты от инфекционных заболеваний, а также создания успокаивающей атмосферы.
Многогранники из модулей в виде изогнутого особым образом параллелограмма, были разработаны в 1960-х годах японским оригамистом Мицунобу Сонобе и названы в его честь. Идею мастер, скорее всего, позаимствовал у своего предшественника Хаято Охоко, в 1734 году впервые описавшего и представившего схему трёхмерного куба из нескольких одинаковых элементов.
Оригами из треугольных модулей – изобретение китайских мастеров. Его истоки точно неизвестны, но западному миру пришлось познакомиться с этой уникальной техникой при весьма печальных обстоятельствах. В 1993 году на борту грузового судна Golden Venture в Соединённые Штаты прибыли 286 нелегальных эмигрантов из Китая. «Новая родина» встретила их неласково. Когда корабль сел на мель неподалёку от нью-йоркского пляжа Рокуэй-Бич, пассажиры попытались добраться до «земли обетованной» вплавь, причём 10 из них утонули. Остальные нелегалы были арестованы Службой иммиграции и натурализации (INS) и разбросаны по тюрьмам в разных концах Америки.
В ожидании ответа на просьбу о предоставлении убежища, китайские заключённые коротали время за национальными видами рукоделия, в том числе и оригами, которое на пиньине называется «жэжи». В процессе работы нелегалы изобрели треугольные модули, создавая из них масштабные фигуры: вазы, лебедей, ананасы и корабли. Вместо обычной бумаги использовали обложки старых журналов и газет. Позднее, когда техника получила распространение, для модульных элементов нередко брали китайские банкноты.
Скульптуры в технике модульного оригами заключённые дарили тем, кто оказывал им поддержку или продавали, чтобы собрать средства на юридические услуги. Часть их представлена на передвижной выставке «Полёт свободы», организованной Американским иммиграционным центром.
Видео:Развертка тетраэдра - это легко! Как сделать объёмную правильную треугольную пирамиду из бумаги?Скачать

Какие ещё бывают треугольники-оригами
Треугольные модули – первое, что приходит на ум, когда речь идёт о технике оригами. Но существуют и другие элементы с аналогичным названием, с которыми желательно познакомиться, чтобы не путаться в понятиях.
«Двойной треугольник»
Китайские модули-оригами иногда путают с популярной базовой фигурой, не имеющей к ним никакого отношения. «Двойной треугольник» или «Водяная бомбочка» применяется в классическом японском бумагоделии, как основа для многих известных моделей. Среди них «Рыбка», «Лягушка», «Кролик» и так далее.
Складывается базовый треугольник оригами по следующей схеме:
Солдатское письмо
Знаменитые «фронтовые треугольники», которые посылали бойцы с передовой во время Великой Отечественной войны, как ни удивительно, тоже сложены в технике оригами. Такой способ позволял обходиться без конверта – адрес писали на внешней стороне листа, а сообщение на внутренней. При этом письмо не мялось и рвалось, каждая его строчка была сохранена для близких людей, с нетерпением ожидавших весточки.
Солдатские треугольники дарили радость, служили лучшим свидетельством того, что их автор жив. А вот письма в настоящих конвертах отправляли только официальные инстанции, извещая о гибели или пропаже без вести. Чтобы проникнуться атмосферой тех лет и сберечь память о подвиге народа в борьбе с немецким нацизмом, «Солдатские треугольники-оригами» часто изготавливают ко Дню победы.
Видео:Как сделать ромб из бумаги. Оригами ромб из бумагиСкачать

Пирамида из бумаги своими руками. Схемы и способы изготовления
Видео:КАК СДЕЛАТЬ ЗВЁЗДЧАТЫЙ ОКТАЭДР? ЗВЁЗДЧАТЫЙ ОКТАЭДР. ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ ИЗ БУМАГИ. | #RAIDOTVСкачать

Как сделать объемные геометрические фигуры
Дети познают мир в процессе игры и творчества. Трехмерные фигуры, выполненные своими руками, помогут познакомиться с удивительной наукой — геометрией.
Примеры трафаретов и шаблонов можно скачать из Интернета и распечатать. Затем все фигуры вырезают и склеивают. Дети старшего возраста могут самостоятельно нарисовать развертку нужной фигуры, малышам помогают родители,.
Геометрические объекты делают из бумаги (белой или цветной), картона. Из последнего материала они получаются плотными и прочными.
Из бумаги

к оглавлению ^
Из картона

к оглавлению ^
Развертки куба





Треугольника


Прямоугольника


Цилиндра

к оглавлению ^
Ромба

к оглавлению ^
Призмы








Видео:🤦♂️Пять тетраэдров оригами (Thomas Hull), Five Origami tetrahedronsСкачать

Задание 2 (построение прямоугольного треугольника)
Постройте на нелинованной бумаге треугольник , чтобы угол был прямым, длина стороны равнялась 15 см, а длина сторогы – 20 см.
Построим точку (Рис. 18).
Проведем через точку прямую (Рис. 19).
Рис. 19. Прямая, проведенная через точку
Для построения прямого угла воспользуемся прямоугольным треугольником. Приложим треугольник так, чтобы вершина прямого угла совпала с точкой , а одна из сторон совпала с лучом, как показано на рис. 20.
Рис. 20. Построение прямого угла
Проведем по второй стороне прямого угла треугольника луч из точки и получим прямой угол (Рис. 21).
Рис. 21. Полученный прямой угол
Выполним построение сторон треугольника. Построим отрезок , который равен 15 см (Рис. 22).
Построим отрезок , который равен 20 см (Рис. 23).
Соединим полученные точки отрезком . Мы получили прямоугольный треугольник (Рис. 24) с прямым углом и сторонами см и см.
Рис. 24. Треугольник
Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Схемы для вырезания
Ученикам 1–2 класса демонстрируют в школе простые геометрические фигуры и 3d: квадрат, кубик, прямоугольник. Их несложно вырезать и склеить. Шаблоны развивают мелкую моторику у детей и дают первые представления о геометрии.
Ученики средней школы, которые изучают черчение, делают сложные фигуры: бумажные шестигранники, фигуры из пятиугольников, цилиндры. Из бумаги для детей выполняют домики для кукол, мебель, оригами, замок для маленьких игрушек, маски на лицо (трехмерные называются полигональными).
Конуса


Пирамиды



Шестигранника


Макета с припусками

к оглавлению ^
Параллелепипеда


Трапеции


Овала

к оглавлению ^


Материал, из чего можно сделать плотный шар — картон или плотная бумага.
Многогранника


Параллелограмма

к оглавлению ^
Видео:Учим плоские геометрические фигуры с паровозиком Чух-Чухом - часть первая (1). Геометрия для детейСкачать

Задание 1 (определение вида треугольников)
Назовите номера тупоугольных, остроугольных и прямоугольных треугольников на рисунке 16.
Рис. 16. Иллюстрация к заданию 1
Треугольник номер 1 – остроугольный, у него все углы острые. Треугольники номер 3 и 4 – тупоугольные, каждый из них имеет один тупой угол. Фигура номер 2 – прямоугольный треугольник. Проверим, действительно ли эта фигура имеет прямой угол, с помощью прямоугольного треугольника (Рис. 17).
Рис. 17. Проверка треугольника номер 2
Мы видим, что вершины и стороны прямого угла совпали, значит, угол прямой, а треугольник прямоугольный.
Видео:Как сделать объемную ТРЕУГОЛЬНУЮ ПРИЗМУ из бумаги А4? // Геометрические фигуры своими рукамиСкачать

Шаблоны для склеивания
Зачастую школьники задаются вопросом, что можно сделать из бумаги к урокам труда или на выставку. Работы ученика выделятся среди остальных, если это будут сложные трехмерные предметы, рельефные геометрические фигуры, платоновы тела, шаблоны кристаллов и минералов.
Если следовать инструкции, то ученик 5–6 класса сможет без помощи родителей сделать точный додекаэдр или тетраэдр.
Иногда в школе задают логические задания, как из квадрата сделать круг или шестиугольник. Для этого определить центр квадрата, согнув его по диагонали. Точка пересечения прямых — центр квадрата и будущего круга. Исходя из этого, можно начертить круг.
Сложных фигур

к оглавлению ^

к оглавлению ^
Октаэдра


Тетраэдра


Икосаэдра


Додекаэдра



Гексаэдра

к оглавлению ^
Фигурок из треугольников

к оглавлению ^
Видео:Пирамида из бумаги/Paper pyramid/DIYСкачать

Виды углов
Развернутый угол. (Рис. 4)
Угол называется развернутым, если его стороны лежат на одной прямой.
Рис. 4. Виды углов: развернутый
Прямой угол (Рис. 5)
Прямой угол составляет половину развернутого.
Рис. 5. Виды углов: прямой угол
Прямой угол можно получить путем складывания бумаги. Сложив лист дважды, мы получим модель прямого угла, его составляют линии сгиба.
Приложим модель угла к углу на чертеже (Рис. 5) таким образом, чтобы углы и стороны совпали (Рис. 6).
| Рис. 5. Модель угла и угол на чертеже | Рис. 6. Модель угла, приложенная к углу на чертеже |
Мы убедились, что на чертеже действительно изображен прямой угол.
Для удобства определения, прямой угол или нет, используют особый инструмент – прямоугольный треугольник (Рис. 7).
Рис. 7. Прямоугольный треугольник
Непрямые углы делятся на острые (Рис. 
| Рис. 8. Виды углов: острый угол Острый угол меньше прямого (Рис. 10). |
Рис. 10. Сравнение острого и прямого угла
Тупой угол больше прямого (Рис. 12).
Рис. 12. Сравнение тупого и прямого угла
Видео:оригами пирамида как сделать пирамиду из бумаги схема пирамида хеопса How to make Paper PyramidСкачать

Макеты из бумаги
Макетирование — увлекательное занятие. Оно помогает развить воображение и логическое мышление. Из бумаги делают не только фигуры, но и необычные скульптуры, статуэтки, шестиугольные–двенадцатиугольные предметы, наклонные объекты (например, Пизанскую башню), карандаши, линейки. На фото и картинках можно посмотреть, как выглядят оригинальные поделки из бумаги.
Школьники младших классов или дошколята делают бумажные объемные поделки. Например, предметы из овала — веер, цветы, гусеницы. Для них потребуются овалы и круги разного диаметра. Раскладки склеиваются между собой, получаются трехмерные игрушки.
Оригами

к оглавлению ^



Животные

к оглавлению ^
Корабль
Применяется множество вариантов, как сделать кораблик из бумаги.

к оглавлению ^
Полигональные чертежи

к оглавлению ^
Игрушки из фигур

к оглавлению ^
Геометрические маски


Карандаш

к оглавлению ^
Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Многогранники. Виды многогранников и их свойства
Многогранники не только занимают видное место в геометрии, но и встречаются в повседневной жизни каждого человека. Не говоря уже об искусственно созданных предметах обихода в виде различных многоугольников, начиная со спичечного коробка и заканчивая архитектурными элементами, в природе также встречаются кристаллы в форме куба (соль), призмы (хрусталь), пирамиды (шеелит), октаэдра (алмаз) и т. д.
Видео:ОРИГАМИ ПИРАМИДА | Как сделать пирамиду из бумаги | Геометрические фигуры из бумагиСкачать

Понятие многогранника, виды многогранников в геометрии
Геометрия как наука содержит раздел стереометрию, изучающую характеристики и свойства объёмных фигуры. Геометрические тела, стороны которых в трёхмерном пространстве образованы ограниченными плоскостями (гранями), носят название «многогранники». Виды многогранников насчитывают не один десяток представителей, отличающихся количеством и формой граней.
Тем не менее у всех многогранников есть общие свойства:
- Все они имеют 3 неотъемлемых компонента: грань (поверхность многоугольника), вершина (углы, образовавшиеся в местах соединения граней), ребро (сторона фигуры или отрезок, образованный в месте стыка двух граней).
- Каждое ребро многоугольника соединяет две, и только две грани, которые по отношению друг к другу являются смежными.
- Выпуклость означает, что тело полностью расположено только по одну сторону плоскости, на которой лежит одна из граней. Правило применимо ко всем граням многогранника. Такие геометрические фигуры в стереометрии называют термином выпуклые многогранники. Исключение составляют звёздчатые многогранники, которые являются производными правильных многогранных геометрических тел.
Многогранники можно условно разделить на:
- Виды выпуклых многогранников, состоящих из следующих классов: обычные или классические (призма, пирамида, параллелепипед), правильные (также называемые Платоновыми телами), полуправильные (второе название – Архимедовы тела).
- Невыпуклые многогранники (звёздчатые).
Видео:Как сделать объёмный ромб из бумаги. Геометрические фигуры оригами. Октаэдр.Скачать

Призма и её свойства
Стереометрия как раздел геометрии изучает свойства трёхмерных фигур, виды многогранников (призма в их числе). Призмой называют геометрическое тело, которое имеет обязательно две совершенно одинаковые грани (их также называют основаниями), лежащие в параллельных плоскостях, и n-ое число боковых граней в виде параллелограммов. В свою очередь, призма имеет также несколько разновидностей, в числе которых такие виды многогранников, как:
- Параллелепипед — образуется, если в основании лежит параллелограмм — многоугольник с 2 парами равных противоположных углов и двумя парами конгруэнтных противоположных сторон.
- Прямая призма имеет перпендикулярные к основанию рёбра.
- Наклонная призма характеризуется наличием непрямых углов (отличных от 90) между гранями и основанием.
- Правильная призма характеризуется основаниями в виде правильного многоугольника с равными боковыми гранями.
Основные свойства призмы:
- Конгруэнтные основания.
- Все рёбра призмы равны и параллельны по отношению друг к другу.
- Все боковые грани имеют форму параллелограмма.
Видео:Многоугольники. Математика 8 класс | TutorOnlineСкачать

Пирамида
Пирамидой называют геометрическое тело, которое состоит из одного основания и из n-го числа треугольных граней, соединяющихся в одной точке – вершине. Следует отметить, что если боковые грани пирамиды представлены обязательно треугольниками, то в основании может быть как треугольный многоугольник, так и четырёхугольник, и пятиугольник, и так до бесконечности. При этом название пирамиды будет соответствовать многоугольнику в основании. Например, если в основании пирамиды лежит треугольник – это треугольная пирамида, четырёхугольник – четырёхугольная, и т. д.
Пирамиды – это конусоподобные многогранники. Виды многогранников этой группы, кроме вышеперечисленных, включают также следующих представителей:
- Правильная пирамида имеет в основании правильный многоугольник, и высота ее проектируется в центр окружности, вписанной в основание или описанной вокруг него.
- Прямоугольная пирамида образуется тогда, когда одно из боковых рёбер пересекается с основанием под прямым углом. В таком случае это ребро справедливо также назвать высотой пирамиды.
- В случае если все боковые рёбра пирамиды конгруэнтны (одинаковой высоты), то все они пересекаются с основанием под одним углом, а вокруг основания можно прочертить окружность с центром, совпадающим с проекцией вершины пирамиды.
- Если в основании пирамиды лежит правильный многоугольник, то все боковые рёбра конгруэнтны, а грани являются равнобедренными треугольниками.
Видео:КАК СДЕЛАТЬ ШЕСТИУГОЛЬНУЮ ПИРАМИДУ ИЗ БУМАГИ? ШЕСТИУГОЛЬНАЯ ПИРАМИДА. ОБЪЕМНЫЕ ГЕОМЕТРИЧЕСКИЕ ФИГУРЫСкачать

Правильный многогранник: виды и свойства многогранников
В стереометрии особое место занимают геометрические тела с абсолютно равными между собой гранями, в вершинах которых соединяется одинаковое количество рёбер. Эти тела получили название Платоновы тела, или правильные многогранники. Виды многогранников с такими свойствами насчитывают всего пять фигур:
Своим названием правильные многогранники обязаны древнегреческому философу Платону, описавшему эти геометрические тела в своих трудах и связавшему их с природными стихиями: земли, воды, огня, воздуха. Пятой фигуре присуждали сходство со строением Вселенной. По его мнению, атомы природных стихий по форме напоминают виды правильных многогранников. Благодаря своему самому захватывающему свойству – симметричности, эти геометрические тела представляли большой интерес не только для древних математиков и философов, но и для архитекторов, художников и скульпторов всех времён. Наличие всего лишь 5 видов многогранников с абсолютной симметрией считалось фундаментальной находкой, им даже присуждали связь с божественным началом.
Видео:Сумма внутренних углов многоугольника. Выпуклые и невыпуклые многоугольники. 8 класс.Скачать

Гексаэдр и его свойства
В форме шестигранника преемники Платона предполагали сходство со строением атомов земли. Конечно же, в настоящее время эта гипотеза полностью опровергнута, что, однако, не мешает фигурам и в современности привлекать умы известных деятелей своей эстетичностью.
В геометрии гексаэдр, он же куб, считается частным случаем параллелепипеда, который, в свою очередь, является разновидностью призмы. Соответственно и свойства куба связаны со свойствами призмы с той лишь разницей, что все грани и углы куба равны между собой. Из этого вытекают следующие свойства:
- Все рёбра куба конгруэнтны и лежат в параллельных плоскостях по отношению друг к другу.
- Все грани – конгруэнтные квадраты (всего в кубе их 6), любой из которых может быть принят за основание.
- Все межгранные углы равны 90.
- Из каждой вершины исходит равное количество рёбер, а именно 3.
- Куб имеет 9 осей симметрии, которые все пересекаются в точке пересечения диагоналей гексаэдра, именуемой центром симметрии.
Видео:Как начертить треугольник | 4 способа | Выпуклый многоугольникСкачать

Тетраэдр
Тетраэдр – это четырёхгранник с равными гранями в форме треугольников, каждая из вершин которых является точкой соединения трёх граней.
Свойства правильного тетраэдра:
- Все грани тетраэда – это равносторонние треугольники, из чего следует, что все грани четырёхгранника конгруэнтны.
- Так как основание представлено правильной геометрической фигурой, то есть имеет равные стороны, то и грани тетраэдра сходятся под одинаковым углом, то есть все углы равны.
- Сумма плоских углов при каждой из вершин равняется 180, так как все углы равны, то любой угол правильного четырёхгранника составляет 60.
- Каждая из вершин проецируется в точку пересечения высот противоположной (ортоцентр) грани.
Видео:Как найти периметр данной фигуры? Решение за одну минуту!Скачать

Октаэдр и его свойства
Описывая виды правильных многогранников, нельзя не отметить такой объект, как октаэдр, который визуально можно представить в виде двух склеенных основаниями четырёхугольных правильных пирамид.
- Само название геометрического тела подсказывает количество его граней. Восьмигранник состоит из 8 конгруэнтных равносторонних треугольников, в каждой из вершин которого сходится равное количество граней, а именно 4.
- Так как все грани октаэдра равны, равны и его межгранные углы, каждый из которых равняется 60, а сумма плоских углов любой из вершин составляет, таким образом, 240.
Додекаэдр
Если представить, что все грани геометрического тела представляют собой правильный пятиугольник, то получится додекаэдр – фигура из 12 многоугольников.
- В каждой вершине пересекаются по три грани.
- Все грани равны и имеют одинаковую длину рёбер, а также равную площадь.
- У додекаэдра 15 осей и плоскостей симметрии, причём любая из них проходит через вершину грани и середину противоположного ей ребра.
Икосаэдр
Не менее интересная, чем додекаэдр, фигура икосаэдр представляет собой объёмное геометрическое тело с 20 равными гранями. Среди свойств правильного двадцатигранника можно отметить следующие:
- Все грани икосаэдра — равнобедренные треугольники.
- В каждой вершине многогранника сходится пять граней, и сумма смежных углов вершины составляет 300.
- Икосаэдр имеет так же, как и додекаэдр, 15 осей и плоскостей симметрии, проходящих через середины противоположных граней.
Полуправильные многоугольники
Кроме Платоновых тел, в группу выпуклых многогранников входят также Архимедовы тела, которые представляют собой усечённые правильные многогранники. Виды многогранников данной группы обладают следующими свойствами:
- Геометрические тела имеют попарно равные грани нескольких типов, например, усечённый тетраэдр имеет так же, как и правильный тетраэдр, 8 граней, но в случае Архимедова тела 4 грани будут треугольной формы и 4 — шестиугольной.
- Все углы одной вершины конгруэнтны.
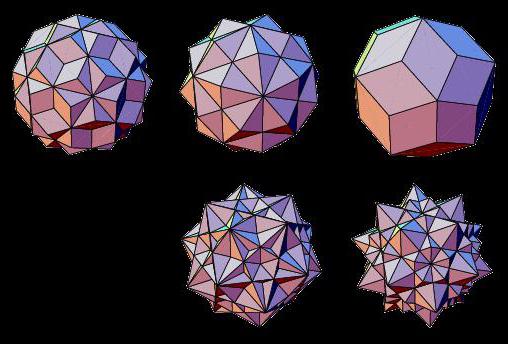
Звёздчатые многогранники
Представители необъёмных видов геометрических тел – звёздчатые многогранники, грани которых пересекаются друг с другом. Они могут быть образованы путём слияния двух правильных трёхмерных тел либо в результате продолжения их граней.
Таким образом, известны такие звёздчатые многогранники, как: звёздчатые формы октаэдра, додекаэдра, икосаэдра, кубооктаэдра, икосододекаэдра.