Объем пирамиды прямоугольный треугольник

На данной странице калькулятор поможет рассчитать объем пирамиды онлайн. Для расчета задайте площадь, высоту, сторону или количество сторон. Вычисления производятся в миллиметрах, сантиметрах, метрах. Результат выводится в кубических сантиметрах, литрах и кубических метров.

Пирамида – многогранник, основание которого – многоугольник, а остальные грани – треугольники, имеющие общую вершину. Пирамида является частным случаем конуса. Пирамида называется правильной, если её основанием является правильный многоугольник, а вершина проецируется в центр основания.

Видео:Объем пирамиды. Практическая часть. 11 класс.Скачать

Пирамида. Прямоугольная пирамида. Правильная пирамида. Объем пирамиды. Тетраэдр

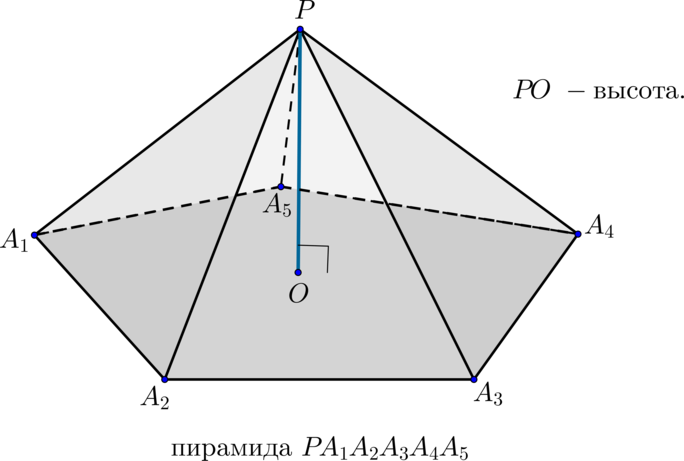
Факт 1. Про произвольную пирамиду (PA_1A_2. A_n)
(bullet) Многоугольник (A_1. A_n) – основание;
треугольники (PA_1A_2, PA_2A_3) и т.д. – боковые грани;
точка (P) – вершина;
отрезки (PA_1, PA_2, . A_1A_2) и т.д. – ребра.
(bullet) Если в основании пирамиды лежит треугольник, то она называется (<color<<small>>>) .
(bullet) (<color<<small>>>) — это треугольная пирамида, все грани которой – равносторонние треугольники.
(bullet) Высота пирамиды – перпендикуляр, опущенный из вершины (P) к основанию.
(bullet) (<color<<small>>>) [<color<<large<V=dfracS_<text>h>>>>] где (S_<text>) – площадь основания, (h) – высота пирамиды.
(bullet) Площадь боковой поверхности – сумма площадей всех боковых граней.
Площадь полной поверхности – сумма площади боковой поверхности и площади основания.

(bullet) Заметим, что принято записывать название пирамиды, начиная с вершины.

Факт 2. Про прямоугольную пирамиду
(bullet) Пирамида называется прямоугольной, если одно из ее боковых ребер ( (SR) ) перпендикулярно основанию (оно же будет и высотой).
(bullet) Грани, образованные этим ребром, будут представлять собой прямоугольные треугольники ( (triangle SMR, triangle SPR) ).

Факт 3. Про правильную пирамиду
(bullet) Пирамида называется правильной, если в основании лежит правильный многоугольник (все углы равны и все стороны равны) и выполнено одно из эквивалентных условий:

(sim) боковые ребра равны;
(sim) высота пирамиды проходит через центр описанной около основания окружности;
(sim) боковые ребра наклонены к основанию под одинаковым углом.
(bullet) Заметим, что у правильных многоугольников центры описанной и вписанной окружностей совпадают.

(bullet) Заметим, что у правильной пирамиды все боковые грани – равные равнобедренные треугольники.
Высота этих треугольников, проведенная из вершины пирамиды, называется апофемой.

Видео:11 класс, 35 урок, Объем пирамидыСкачать

Формула объема пирамиды

Пирамида — многогранник, основанием которого является произвольный многоугольник, а все грани представляют собой треугольники с общей вершиной, являющейся вершиной пирамиды.

Элементы пирамиды

Апофема — высота боковой грани правильной пирамиды, проведённая из её вершины (также апофемой называют длину перпендикуляра, опущенного из середины правильного многоугольника на одну из его сторон);

Боковые грани — треугольники, сходящиеся в вершине;

Боковые ребра — общие стороны боковых граней;

Вершина пирамиды — точка, соединяющая боковые рёбра и не лежащая в плоскости основания;

Высота — отрезок перпендикуляра, проведённого через вершину пирамиды к плоскости её основания (концами этого отрезка являются вершина пирамиды и основание перпендикуляра);

Диагональное сечение пирамиды — сечение пирамиды, проходящее через вершину и диагональ основания;

Основание — многоугольник, которому не принадлежит вершина пирамиды.

Видео:Найти объем правильной треугольной пирамидыСкачать

Объем пирамиды через площадь основания и высоту

Объем пирамиды равен одной трети произведения площади основания S_(ABCDEF) на высоту h (OS)

[ LARGE V = frac cdot S cdot h ]

где:
V — объем пирамиды
S — площадь основания пирамиды
h — высота пирамиды

Видео:Даны вершины пирамиды A, B, C, D. Найдите объём пирамиды и высоту, опущенную на грань ACDСкачать

Калькулятор объема пирамиды через площадь основания и высоту

Видео:Призма и пирамида. Площадь и объем. Вебинар | Математика 10 классСкачать

Объём усечённой пирамиды

Усеченная пирамида — часть пирамиды между ее основанием и этим сечением. Сечение параллельное основанию пирамиды делит пирамиду на две части.

Объем усеченной пирамиды равен одной трети произведения высоты h (OS) на сумму площадей верхнего основания S_{1 (abcdef)} , нижнего основания усеченной пирамиды S_{2 (ABCDEF)} и средней пропорциональной между ними.

[ LARGE V = frac cdot h cdot left( S_1 + sqrt + S_2 right) ]

где:
V — объем пирамиды
S₁ — площадь верхнего основания усеченной пирамиды
S₂ — площадь нижнего основания усеченной пирамиды
h — высота усеченной пирамиды

Видео:№244. Основанием пирамиды DABC является прямоугольный треугольник ABC, у которого гипотенузаСкачать

Калькулятор объема усечённой пирамиды

Видео:Объем пирамиды. Урок 16. Геометрия 11 класс.Скачать

Объём правильной пирамиды

Правильная пирамида — пирамида, в основани, которой лежит правильный многоугольник, а высота проходит через центр вписанной окружности в основание.

Объем правильной пирамиды равен одной трети произведения площади правильного многоугольника, являющегося основанием S _(ABCDEF) на высоту h _(OS)

где:
V — объем пирамиды
a — сторона основания пирамиды
n — количество сторон многоугольника в основании
h — высота усеченной пирамиды

Видео:Объём пирамидыСкачать

Калькулятор объёма правильной пирамиды

Видео:✓ Как решать стереометрию | ЕГЭ-2023. Математика. Профильный уровень. Задание 13 | Борис ТрушинСкачать

Объём правильной треугольной пирамиды

Правильная треугольная пирамида — пирамида, у которой основанием является равносторонний треугольник и грани равные равнобедренные треугольники.

Объем правильной треугольной пирамиды равен одной трети произведения площади правильного треугольника, являющегося основанием S _(ABC) на высоту h _(OS)

где:
V — объем пирамиды
a — сторона основания пирамиды
h — высота пирамиды

Видео:№251. Основанием пирамиды DABC является прямоугольный треугольник с гипотенузой ВС. БоковыеСкачать

Калькулятор объёма правильной треугольной пирамиды

Видео:Профильный ЕГЭ 2024. Задача 1. Прямоугольный треугольник. 10 классСкачать

Объём правильной четырёхугольной пирамиды

Правильная четырехугольная пирамида — пирамида, у которой основанием является квадрат и грани равные равнобедренные треугольники.

Объем правильной четырехугольной пирамиды равен одной трети произведения площади квадрата, являющегося основанием S _(ABCD) на высоту h _(OS)

[ LARGE V = frac h cdot a^2 ]

где:
V — объем пирамиды
a — сторона основания пирамиды
h — высота пирамиды

Видео:🔴 Найдите объём правильной четырёхугольной ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 16 | ШКОЛА ПИФАГОРАСкачать

Калькулятор объёма правильной четырёхугольной пирамиды

Видео:ЕГЭ Задание 14 Объем пирамидыСкачать

Объём тетраэдра

Тетраэдр — пирамида, у которой все грани — равносторонние треугольники.

Объем тетраэдра — равен дроби в числителе которой корень квадратный из двух в знаменателе двенадцать, помноженной на куб длины ребра тетраэдра

где:
V — объем пирамиды
a — сторона основания пирамиды

💥 Видео

ОБЪЕМ ПИРАМИДЫСкачать

Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать

Объем пирамиды. 13 задание ЕГЭСкачать

ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать

ЕГЭ по математике - Объём пирамидыСкачать

11 класс. Геометрия. Объём пирамиды. 28.04.2020.Скачать

Как найти объем. Принцип Кавальери | Ботай со мной #050 | Борис Трушин |Скачать