О центр окружности найти площадь треугольника авс

С помощю этого онлайн калькулятора можно найти площадь треугольника. Для нахождения площади треугольника введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть смотрите ниже.

Видео:2038 центр окружности описанной около треугольника ABC лежит на стороне ABСкачать

Площадь треугольника по основанию и высоте

Любой из сторон треугольника можно называть основанием треугольника. Если основание выбрана, то под словом «высота» понимают высоту треугольника, проведенную к основанию (Рис.1):

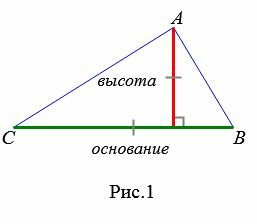Теорема 1. Площадь треугольника равна половине произведения его основания на высоту.

Доказательство. Пусть AC основание треугольника ABC (Рис.2).

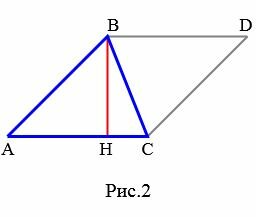Проведем высоту BH. Обозначим через S площадь треугольника. Докажем, что

Из вершины B проведем прямую, параллельную стороне AC, а из C − прямую, параллельную стороне AB. Поскольку ( small AC || BD ) и ( small AB || CD ), то ABDC является параллелограммой и, следовательно, ( small AC = BD ), ( small AB = CD . ) Тогда треугольники ABC и BCD равны по трем сторонам (см. статью на странице Треугольники. Признаки равенства треугольников). Так как площадь параллелограмма ABDC равна ( small S_=AC cdot BH, ) то площадь треугольника ABC (и BCD)равна половине площади параллелограмма:

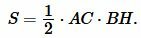Следствие 1. Если высоты треугольников равны, то их площади относятся как основания.

,

,

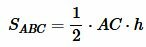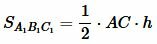Обозначим через k отношение

.

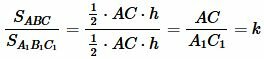То есть отношение площадей треугольников с равными высотами равно отношению их оснований.

Следствие 2. Площадь прямоугольного треугольника равна половине произведения его катетов.

Действительно. Поскольку в прямоугольном треугольнике катеты перпендикулярны друг другу, то один из них можно определить как основание, а другой − как высоту. Тогда по теореме 1, площадь прямоугольного треугольника равна половине произведения его катетов.

Видео:Найдите площадь треугольника АВС, если А(5;2;6), В(1;2;0), С(3;0;3)Скачать

Площадь треугольника по двум сторонам и углу между ними

Теорема 2. Площадь треугольника равна половине произведения двух его сторон на синус угла между ними.

Доказательство. Обозначим через S площадь треугольника ABC и пусть a=BC, b=AC (Рис.3). Докажем, что

.

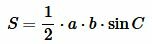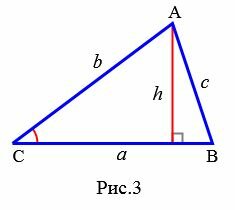Площадь данного треугольника можно вычислить по формуле, полученной выше (теорема 1):

,

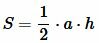(1)

где h − высота треугольника.

,

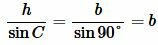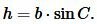(2)

Подставляя (2) в (1), получим:

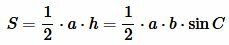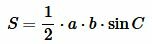(3)

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Площадь треугольника по стороне и прилежащим двум углам

Пусть известна сторона треугольника и две прилежащие углы (Рис.4).

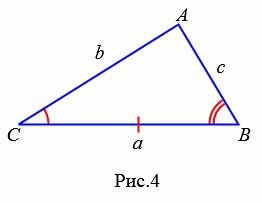Найдем формулу площади этого треугольника. Обозначим через S площадь треугольника. Если у треугольника известны два угла, то можно найти и третий угол:

(4)

Найдем сторону b используя теорему синусов:

,

.

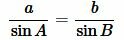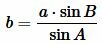(5)

В предыдующем параграфе мы вывели площадь треугольника по двум сторонам и углу между ними. Подставляя (4) и (5) в (3), получим:

.

.

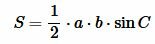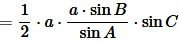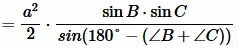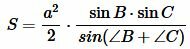(6)

Видео:Задание 24 Площадь описанного треугольникаСкачать

Площадь треугольника по трем сторонам. Формула Герона

Для нахождения площади треугольника по трем сторонам используют формулу Герона:

,

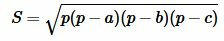(7)

где a, b, c − стороны треугольника, а p − полупериод треугольника:

.

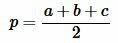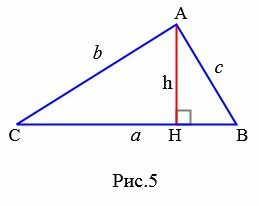Доказательство формулы Герона. На рисунке 5 треугольник ABC имеет стороны a=BC, b=AC, c=AB. Проведем высоту h=AH. Обозначим x=CH. Тогда BH=a−x. Применим теорему Пифагора для треугольников AHC и AHB:

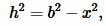(8)

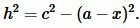(9)

Из (8) и (9) следует:

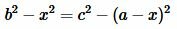Откуда находим x:

,

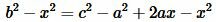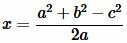(10)

Подставляя (10) в (8) найдем h:

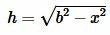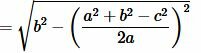(11)

Тогда площадь треугольника равна:

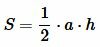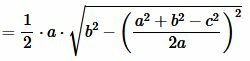(12)

Преобразовав (12) получим формулу (7):

.

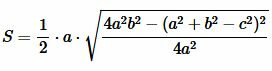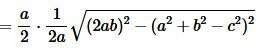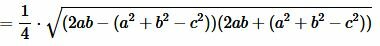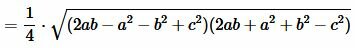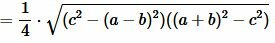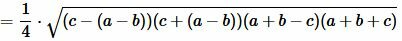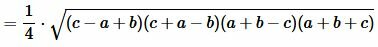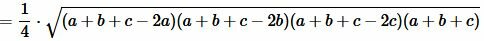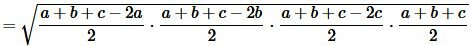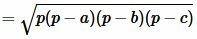Видео:Длина окружности. Площадь круга. 6 класс.Скачать

Площадь треугольника по трем сторонам и радусу описанной окружности

Пусть известны все три стороны треугольника и радиус описанной окружности (Рис.6). Докажем, что площадь треугольника равна: ( small S=frac. )

Видео:Площадь треугольника. Как найти площадь треугольника?Скачать

(50 + БАЛЛОВ ЗА ПОДРОБНЫЙ ОТВЕТ) О — центр окружности, описанной около треугольника ABC, O1 — центр окружности, вписанной в треугольник ABC?

Геометрия | 5 — 9 классы

(50 + БАЛЛОВ ЗА ПОДРОБНЫЙ ОТВЕТ) О — центр окружности, описанной около треугольника ABC, O1 — центр окружности, вписанной в треугольник ABC.

Найти площадь треугольника ABC.

8. проводим из т.

В высоту ВН к АС.

Найдем ОН : для этого рассмотрим треугольник АОН.

Он прямо угольный.

К. треугольник АВС равносторонний, а значит все его углы равны по 60 градусов.

И ОА будет биссектриссой.

По теореме о прямо угольном треугольнике : против угла в 30 градусов лежит катет равный половине гипотенузы.

Значит ОН = 2 Тогда по теореме Пифагора найдем АН : АН ^ 2 = АО ^ 2 — ОН ^ 2.

АН ^ 2 = 16 — 4 = 12 АН = 2корень из 3.

Тогда АС = 2×2 корень из3 = 4 корень из 3.

Найдем S = 1 / 2×АС×ВН = 1 / 2×4 корень из3 × ( 4 + 2) = 2 корень из 3 ×6 = 12 корень из 3

ВН высота, медиана и биссектриса проведенная к АС.

Значит АН = 8 / 2 = 4.

Треугольник АНО прямо угольный .

Пифагора : ОН ^ 2 = 25 — 16 = 9 ОН = 3.

АО = ОВ = 6 радиус .

Тогда АВ = 12 S = 1 / 2×12×6 = 36 А вот 11 и 12 незнаю.

Видео:№203. Через центр О окружности, вписанной в треугольник ABC, проведена прямая ОK, перпендикулярнаяСкачать

Треугольник ABC вписан в окружность?

Треугольник ABC вписан в окружность.

Найти радиус окружности, если AB = 24см, а центр окружности удален от AB на 5см.

Видео:Найти площадь треугольника АВС. Задачи по рисункамСкачать

В треугольнике ABC , угол С = 42 градуса, О — центр вписанной окружности?

В треугольнике ABC , угол С = 42 градуса, О — центр вписанной окружности.

Найти : угол AOB.

Видео:Найдите площадь треугольника на рисунке ★ Два способа решенияСкачать

Вписанный угол ABC = 42 градусам?

Вписанный угол ABC = 42 градусам.

Найти углы треугольника AOC.

(О — ЦЕНТР ОКРУЖНОСТИ).

Видео:ОГЭ 2019. Задание 17. Разбор задач. Геометрия. Окружность.Скачать

Около треугольника ABC описана окружность с центром O?

Около треугольника ABC описана окружность с центром O.

Найдите угол ABC если угол AOC равен 64 градуса.

Видео:Как найти центр круга с помощью подручных средств? ЛЕГКО.Скачать

Центр окружности описанной около равнобедренного треугольника ABC ?

Центр окружности описанной около равнобедренного треугольника ABC .

Является серединой основания треугольника.

Найдите углы треугольника Пожалуйста с решением.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Треугольник ABC вписан в окружность с центром О?

Треугольник ABC вписан в окружность с центром О.

Найдите градусную меру угла С треугольника ABC, если угол AOB равен 63º.

Видео:Радиус описанной окружностиСкачать

В равнобедренный треугольник ABC ( AB = BC ) вписана окружность с центром О ?

В равнобедренный треугольник ABC ( AB = BC ) вписана окружность с центром О .

Найти углы треугольника , если угол BOC = 130.

Видео:Задание 3 ЕГЭ по математике. Урок 41Скачать

Треугольник ABC — остроугольный Описать около треугольника ABC окружность, указать центр и радиусю?

Треугольник ABC — остроугольный Описать около треугольника ABC окружность, указать центр и радиусю.

Видео:Секретные формулы площади треугольникаСкачать

Сторона AC треугольника ABC проходит через центр описанной около него окружности?

Сторона AC треугольника ABC проходит через центр описанной около него окружности.

Найдите угол С, если А = 75.

Видео:ОГЭ Задание 26 Треугольник Вписанная окружность ПлощадьСкачать

Сторона ac треугольника abc проходит через центр описанной около него окружности?

Сторона ac треугольника abc проходит через центр описанной около него окружности.

Найти угол с , если угал aравен 44градусам.

На странице вопроса (50 + БАЛЛОВ ЗА ПОДРОБНЫЙ ОТВЕТ) О — центр окружности, описанной около треугольника ABC, O1 — центр окружности, вписанной в треугольник ABC? из категории Геометрия вы найдете ответ для уровня учащихся 5 — 9 классов. Если полученный ответ не устраивает и нужно расшить круг поиска, используйте удобную поисковую систему сайта. Можно также ознакомиться с похожими вопросами и ответами других пользователей в этой же категории или создать новый вопрос. Возможно, вам будет полезной информация, оставленная пользователями в комментариях, где можно обсудить тему с помощью обратной связи.

1) Рассмотрим треуг. МЕР и треуг. НЕР, т. К. МЕ = ЕН, т. К. МР — диаметр, а угол МЕР( вписанный) на него опирается, значит угол МЕР = 90 * , угол РЕН = 180 * — 90 = 90 * , значит треугольники МЕР = НЕР ( по двум сторонам и углу в 90 * между ними)..

Ответ получается 57.

Клетки, несущие генетическую информацию организма. Участвуют в половом размножении 2 особей разного пола одного вида. При слиянии двух клеток вполовом процессеобразуетсязигота, развивающаяся в особь (или группу особей) с наследственными признаками ..

A = b = 4 c = 4√2 R = 2√2 S = πR² = π(2√2)² = 8π.

Vц = п * R ^ 2 * h. Исходя из формулы получаем, что объем второго цилиндра сначала в 4 раза больше (т. К. радиус в квадрате), а затем в 5 раз меньше. Получаем, что V2 = 15 * 4 : 5 = 12.

Это двадцать знаков.

Возьму к примеру — автобус. «Правила поведения при езде в автобусе» — не нужно разговаривать отвлекать водителя от дороги — не толкаться — уступать место пожилым людям — быть вежливым с пассажирами — платить за проезд вовремя — быть бдительным (сл..

Автобус : В автобусе нельзя толкаться , всегда уступать место старшему , не кричать когда разговаривает разговариваешь по телефону .

Sin B = AC / AB = 3 / 5 = 0. 6.

Не уверена на 100%, но мое решение такое : если я правильно поняла, то углы AMN и NMB показаны как равные. Это означает, что они по 45°, т. К. треугольники прямоугольные. Отсюда исходит, что углы MAN и MBN так же по 45°. Значит катеты прямоугольн..

Видео:КАК НАЙТИ ПЛОЩАДЬ КРУГА, ЕСЛИ ИЗВЕСТЕН ДИАМЕТР? Примеры | МАТЕМАТИКА 6 классСкачать

Как найти площадь треугольника

О чем эта статья:

8 класс, 9 класс

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Видео:Геометрия 8 класс (Урок№10 - Площадь треугольника.)Скачать

Основные понятия

Треугольник — это геометрическая фигура, которая получилась из трех отрезков. Их соединили тремя точками, не лежащими на одной прямой. Отрезки принято называть сторонами, а точки — вершинами.

Площадь — это численная характеристика, которая дает нам информацию о размере части плоскости, ограниченной замкнутой геометрической фигурой.

Если значения заданы в разных единицах измерения длины, мы не сможем узнать, какая площадь треугольника получится. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.

Популярные единицы измерения площади:

• квадратный миллиметр (мм 2 );
• квадратный сантиметр (см 2 );
• квадратный дециметр (дм 2 );
• квадратный метр (м 2 );
• квадратный километр (км 2 );
• гектар (га).

Видео:Как найти площадь треугольника без формулы?Скачать

Формула площади треугольника

Для решения задач применяются различные формулы, в зависимости от известных исходных данных. Далее мы рассмотрим способы решения для всех типов треугольников, в том числе частные случаи для равносторонних, равнобедренных и прямоугольных фигур.

Быстро вычислить площадь треугольника поможет наш онлайн-калькулятор. Просто введите известные вам значения и получите ответ в метрах, сантиметрах или миллиметрах.

Научиться быстро щелкать задачки на нахождение площади треугольника помогут курсы по математике от Skysmart!

Видео:ОГЭ Задание 26 Площадь треугольникаСкачать

Общая формула

1. Площадь треугольника через основание и высоту

, где — основание, — высота.

2. Площадь треугольника через две стороны и угол между ними

, где , — стороны, — угол между ними.

3. Площадь треугольника через описанную окружность и стороны

, где , , — стороны, — радиус описанной окружности.

4. Площадь треугольника через вписанную окружность и стороны

, где , , — стороны, — радиус вписанной окружности.

Если учитывать, что — это способ поиска полупериметра, то формулу можно записать следующим образом:

5. Площадь треугольника по стороне и двум прилежащим углам

, где — сторона, и — прилежащие углы.

6. Формула Герона для вычисления площади треугольника

Сначала необходимо подсчитать разность полупериметра и каждой его стороны. Потом найти произведение полученных чисел, умножить результат на полупериметр и найти корень из полученного числа.

, где , , — стороны, — полупериметр, который можно найти по формуле:

Для прямоугольного треугольника

Площадь треугольника с углом 90° по двум сторонам

Площадь треугольника по гипотенузе и острому углу

, где — гипотенуза, — любой из прилегающих острых углов.

Гипотенузой принято называть сторону, которая лежит напротив прямого угла.

Площадь прямоугольного треугольника по катету и прилежащему углу

, где — катет, — прилежащий угол.

Катетом принято называть одну из двух сторон, образующих прямой угол.

Площадь треугольника через гипотенузу и радиус вписанной окружности

, где — гипотенуза, — радиус вписанной окружности.

Площадь треугольника по отрезкам, на которые делит вписанная окружность его гипотенузу

, где , — части гипотенузы.

Площадь прямоугольного треугольника по формуле Герона

, где , — катеты, — полупериметр, который можно найти по формуле:

Для равнобедренного треугольника

Вычисление площади через основание и высоту

, где — основание, — высота, проведенная к основанию.

Поиск площади через боковые стороны и угол между ними

, где — боковая сторона, — угол между боковыми сторонами.

Площадь равностороннего треугольника через радиус описанной окружности

, где — радиус описанной окружности.

Площадь равностороннего треугольника через радиус вписанной окружности

, где — радиус вписанной окружности.

Площадь равностороннего треугольника через сторону

Площадь равностороннего треугольника через высоту

Таблица формул нахождения площади треугольника

У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу, использовать как закладку в тетрадке или учебнике и обращаться к ней по необходимости.