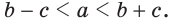Неравенство треугольника матанализ с модулями

Содержание:

Неравенство треугольника:

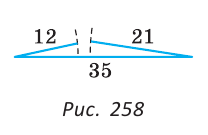
Опыт нам подсказывает, что путь из точки А в точку С по прямой АС короче, чем по ломаной ABC (рис. 255), т. е. АС 12+21 (рис. 258).

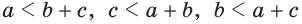
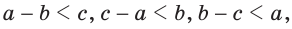
Замечание. Из неравенств треугольника следует, что то есть любая сторона треугольника больше разности двух других его сторон. Так, для стороны а справедливо

Пример:

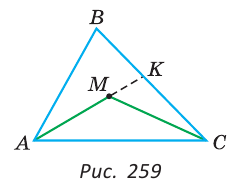
Внутри треугольника ABC взята точка М (рис. 259). Доказать, что периметр треугольника АМС меньше периметра треугольника ABC.

Решение:

Так как у треугольников ABC и АМС сторона АС — общая, то достаточно доказать, что AM + МС B (рис. 108, а).

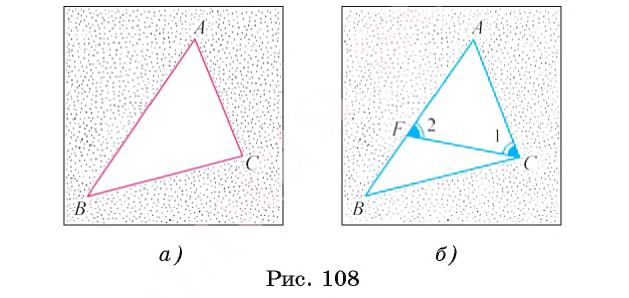
2) Отложим на стороне АВ отрезок АF, равный стороне AC (рис. 108, б).

3) Так как АF 1.

4) Угол 2 является внешним углом треугольника ВFС, следовательно, 2 > B.

5) Так как треугольник FАС является равнобедренным, то 1 = 2.

Таким образом, BСА > 1, 1 = 2 и 2 > B.

Отсюда получаем, что ВСА > B.

Теорема 2. В треугольнике против большего угла лежит большая сторона.

1) Пусть в треугольнике АBС С > B. Докажем, что АВ > АС (см. рис. 108, а). Доказательство проведем методом от противного.

2) Предположим, что это не так. Тогда: либо АВ = АС, либо АВ C.

В каждом из этих случаев получаем противоречие с условием: C > B. Таким образом, сделанное предположение неверно и, значит, АВ > АС.

Из данной теоремы следует утверждение: в прямоугольном треугольнике катет меньше гипотенузы.

Действительно, гипотенуза лежит против прямого угла, а катет — против острого. Поскольку прямой угол больше острого, то по теореме 2 получаем, что гипотенуза больше катета.

Теорема 3 (признак равнобедренного треугольника). Если два угла треугольника равны, то треугольник равнобедренный.

Пусть в треугольнике два угла равны. Тогда равны стороны, лежащие против этих углов. В самом деле, если предположить, что одна из указанных сторон больше другой, то по теореме 1 угол, лежащий против этой стороны, будет больше угла, лежащего против другой стороны, что противоречит условию равенства углов.

Значит, наше предположение неверно и в треугольнике две стороны равны, т. е. треугольник является равнобедренным.

Неравенство треугольника

Докажем, что длина каждой стороны треугольника меньше суммы длин двух других сторон.

Теорема 4. Длина каждой стороны треугольника меньше суммы длин двух других его сторон.

1) Пусть ABC — произвольный треугольник. Докажем, например, что выполняется неравенство АВ l, следовательно, верно неравенство АВF > 2.

4) Так как в треугольнике против большего угла лежит большая сторона (теорема 2), то АВ

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Видео:Неравенства с модулем | Математика | TutorOnlineСкачать

Модуль

В этой статье введем и очень подробно разберем такое важное понятие, как модуль числа. Разберемся, откуда модуль взялся, какими свойствами обладает. Научимся решать уравнения и неравенства с модулем.

Видео:Доказательство свойств модуля, №25.Скачать

«Величина» числа

Сначала попытаемся сформулировать понятие о «величине» числа. Из этого понятия естественным образом получим понимание, откуда взялся и как определить модуль.

Геометрический смысл

Представьте, что вы стоите в точке 0 на числовой оси. Слева от вас, в точке − 1 0 0 , находится школа. Справа, в точке 5 0 , находится ваш дом. Математически число − 1 0 0 меньше, чем 5 0 . Но вот идти до школы 1 0 0 метров влево гораздо дольше, чем пройти 5 0 метров до дома вправо. В этом смысле «величина» пройденного расстояния в − 1 0 0 метров больше, чем 5 0 метров.

Пусть теперь школа находится в точке − 1 0 , а дом в точке 1 0 . Математически вновь получаем, что − 1 0 меньше 1 0 . Но вот нам, находящимся в 0 , совершенно нет разницы: идти − 1 0 метров влево или 1 0 метров вправо. В обоих случаях мы пройдем 1 0 метров. То есть, по «величине» числа − 1 0 и 1 0 равны.

Количественный смысл

Рассмотрим числа 5 0 и − 1 0 0 . В математическом смысле − 1 0 0 гораздо меньше 5 0 . А давайте посмотрим на эти числа под другим углом. У вас есть всего 5 0 рублей и вы задолжали другу. Ваш долг составляет − 1 0 0 рублей. В этом смысле «величина» вашего долга в − 1 0 0 рублей гораздо больше имеющихся у вас 5 0 рублей. Получается, что математически − 1 0 0 меньше 5 0 , но по «величине» − 1 0 0 больше 5 0 .

Теперь рассмотрим числа − 1 0 и 1 0 . Математически, опять же, − 1 0 меньше 1 0 . Но, пользуясь нашей аналогией с долгом, своими 1 0 рублями вы полностью покроете долг в − 1 0 рублей. То есть, по «величине» число − 1 0 равно числу 1 0 .

Понятие величины

Мы поняли, что каждое число имеет свою «величину». Причем эта величина не зависит от того, положительным или отрицательным является число. Можно даже сказать, что «величина» числа это и есть само число, от которого «отбросили» его знак.

Видео:✓ Неравенство треугольника | Ботай со мной #126 | Борис ТрушинСкачать

Модуль числа

Сформулируем на строгом языке математики наше интуитивное представление о «величине» числа, которое мы сформировали в предыдущем разделе.

Модуль или абсолютная величина вещественного числа x — само число x , если оно неотрицательно, иначе − x .

Допустим, мы хотим найти модуль какого-то числа a . Согласно определению, нам надо провести элементарную проверку. Если число a положительное или равно 0 , то модулем a и является само a . Если же a меньше 0 , то результатом модуля будет − a .

∣ 5 ∣ = 5 ∣ 0 ∣ = 0 ∣ − 1 2 ∣ = − ( − 1 2 ) = 1 2

Легко убедиться, что модуль числа полностью соответсвует по смыслу «величине» числа, рассмотренной в предыдущем разделе. Там мы утверждали, что по «величине» − 1 0 0 больше 5 0 , а − 1 0 равно 1 0 . И действительно:

∣ − 1 0 0 ∣ = 1 0 0 ∣ − 1 0 ∣ = 1 0 ​ ∣ 5 0 ∣ = 5 0 ∣ − 1 0 0 ∣ > ∣ 5 0 ∣ ∣ 1 0 ∣ = 1 0 ∣ − 1 0 ∣ = ∣ 1 0 ∣ ​

Положение знака нестрогого неравенства в определении модуля не имеет значения:

Обозначим второе определение модуля числа x как ∣ x ∣ ′ . Покажем, что какой x не возьми, будет выполняться ∣ x ∣ = ∣ x ∣ ′ .

Пусть x > 0 . По классическому определению ∣ x ∣ = x . По второму: ∣ x ∣ ′ = x . То есть ∣ x ∣ = ∣ x ∣ ′ .

Пусть x = 0 . По классическому определению ∣ 0 ∣ = 0 . А вот во втором определении 0 попадает уже под второе условие, то есть ∣ 0 ∣ ′ = − 0 = 0 . Опять имеем ∣ 0 ∣ = ∣ 0 ∣ ′ .

Наконец, пусть x 0 . По классическому определению ∣ x ∣ = − x . У второго определения та же ситуация: ∣ x ∣ ′ = − x . Получается, что и в этом случае ∣ x ∣ = ∣ x ∣ ′ .

Итак, мы рассмотрели все возможные значения для x и во всех случаях ∣ x ∣ = ∣ x ∣ ′ . Это и означает, что между двумя определениями нет никакой разницы ■

Такое определение иногда бывает полезно. Например, если x лежит в следующих пределах: − 1 0 ≤ x ≤ 0 , то можно сразу сказать, что ∣ x ∣ = − x , даже несмотря на то, что для x = 0 так выражаться будет некорректно, ведь ∣ 0 ∣ = 0 , а не − 0 .

Видео:Метод рационализации. Неравенства с модулямиСкачать

Свойства модуля

У модуля есть очень много полезных свойств, которые сильно помогают при решении уравнений, неравенств, доказательстве теорем и так далее. Рассмотрим самые полезные из них. Все свойства ниже формулируем для любых вещественных чисел x и y .

Очевидные свойства

Наиболее очевидные свойства модуля напрямую вытекают из рассмотренного ранее понятия о «величине» числа. Например, мы определили «величину» числа как само число с «отброшенным» знаком. Это означает, что «величина» не может быть отрицательной.

Видео:7 класс, 34 урок, Неравенство треугольникаСкачать

Неравенство треугольника: доказательство, примеры, решенные упражнения

Неравенство треугольника: доказательство, примеры, решенные упражнения — Наука

Видео:Неравенства треугольника. 7 класс.Скачать

Содержание:

Это называется неравенство треугольника к свойству двух действительных чисел, заключающемуся в том, что абсолютное значение их суммы всегда меньше или равно сумме их абсолютных значений. Это свойство также известно как неравенство Минковского или треугольное неравенство.

Это свойство чисел называется треугольным неравенством, потому что в треугольниках длина одной стороны всегда меньше или равна сумме двух других, даже если это неравенство не всегда применяется в области треугольников.

Существует несколько доказательств треугольного неравенства в действительных числах, но в этом случае мы выберем одно, основанное на свойствах абсолютного значения и биномиального квадрата.

Теорема: Для каждой пары чисел к Y б относящиеся к действительным числам, он должен:

Видео:Математика это не ИсламСкачать

Демонстрация

Начнем с рассмотрения первого члена неравенства, который возведем в квадрат:

| a + b | ^ 2 = (a + b) ^ 2 = a ^ 2 + 2 a b + b ^ 2 (уравнение 1)

На предыдущем шаге мы использовали свойство, согласно которому любое число в квадрате равно абсолютному значению указанного числа в квадрате, то есть:| х | ^ 2 = х ^ 2. Также использовалось квадратное биномиальное разложение.

Все номера Икс меньше или равно его абсолютному значению. Если число положительное, оно равно, но если число отрицательное, оно всегда будет меньше положительного числа. В этом случае его собственное абсолютное значение, то есть можно сказать, что x ≤ | х |.

Продукт (а б) является числом, поэтому применяется, что (а б) ≤ | а б |. Когда это свойство применяется к (уравнение 1), мы имеем:

| a + b | ^ 2 = a ^ 2 + 2 (a b) + b ^ 2 ≤ a ^ 2 + 2 | а б | + b ^ 2 (уравнение 2)

Учитывая, что | a b | = | а || б | la (уравнение 2) можно записать следующим образом:

| a + b | ^ 2 ≤ a ^ 2 + 2 | а || б | + b ^ 2 (уравнение 3)

Но поскольку мы говорили ранее, что квадрат числа равен абсолютному значению квадрата числа, то уравнение 3 можно переписать следующим образом:

| a + b | ^ 2 ≤ | a | ^ 2 + 2 | a | | б | + | b | ^ 2 (уравнение 4)

Во втором члене неравенства признается замечательный продукт, применение которого приводит к:

| a + b | ^ 2 ≤ (| a | + | b |) ^ 2 (уравнение 5)

В предыдущем выражении следует отметить, что значения, которые должны быть возведены в квадрат в обоих членах неравенства, положительны, поэтому необходимо также убедиться, что:

| а + б | ≤ (| a | + | b |) (уравнение 6)

Вышеприведенное выражениеэто именно то, что хотели продемонстрировать.

Видео:Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

Примеры

Далее мы проверим треугольное неравенство на нескольких примерах.

Видео:Как решить неравенства с модулем?Скачать

Пример 1

Мы берем значение a = 2 и значение b = 5, то есть оба положительных числа, и проверяем, выполняется ли неравенство.

Равенство проверено, следовательно, теорема о неравенстве треугольника выполнена.

Видео:Как решать неравенства с модулем. Два модуля в неравенстве.Скачать

Пример 2

Выбираются следующие значения a = 2 и b = -5, то есть положительное число, а другое отрицательное, проверяем, выполняется неравенство или нет.

Неравенство выполнено, следовательно, теорема о треугольном неравенстве проверена.

Видео:Вариант Nº2 - Уровень сложности реального ЕГЭ2024 | Математика профильСкачать

Пример 3

Берём значение a = -2 и значение b = 5, то есть отрицательное число, а другое положительное, проверяем, выполняется ли неравенство.

Неравенство проверено, значит, теорема выполнена.

Видео:Встреча с Путиным в общежитии МГУ на Воробьевых горах!Скачать

Пример 4

Выбираются следующие значения a = -2 и b = -5, то есть оба отрицательные числа, и мы проверяем, выполняется неравенство или нет.

Равенство проверено, следовательно, теорема о неравенстве Минковского выполнена.

Видео:Свойства модуля: линейность, неравенство треугольника, модуль разности модулейСкачать

Пример 5

Мы берем значение a = 0 и значение b = 5, то есть число ноль, а другое положительное, затем проверяем, выполняется неравенство или нет.

Равенство выполнено, следовательно, теорема о неравенстве треугольника проверена.

Видео:НЕРАВЕНСТВА С МОДУЛЕМ 😉 ЧАСТЬ I #shorts #математика #егэ #огэ #профильныйегэСкачать

Пример 6

Мы берем значение a = 0 и значение b = -7, то есть число ноль, а другое положительное, затем проверяем, выполняется неравенство или нет.

Равенство проверено, следовательно, теорема о треугольном неравенстве выполнена.

Видео:✓ Теорема Кантора — Гейне | Равномерная непрерывность | матан #023 | Борис ТрушинСкачать

Решенные упражнения

В следующих упражнениях изобразите геометрически неравенство треугольника или неравенство Минковского для чисел a и b.

Число a будет представлено как сегмент на оси X, его начало O совпадает с нулем оси X, а другой конец сегмента (в точке P) будет в положительном направлении (вправо) от оси X, если > 0, но если a 0), а точка Q будет | b | единиц слева от P, если b Предыдущая статья

🎦 Видео

Уравнение с модулемСкачать

Как раскрыть модуль. Неравенство и график с модулем ЕГЭСкачать

МодульСкачать

МОДУЛЬ 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

9 класс, 5 урок, Неравенства с модулямиСкачать