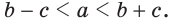Неравенство периметров двух треугольников

Треугольник − это геометрическая фигура, образованная соединением отрезками трех, не лежащих на одной прямой точек .

Эти точки называются вершинами треугольника. Отрезки, соединяющие эти точки называются сторонами треугольника.

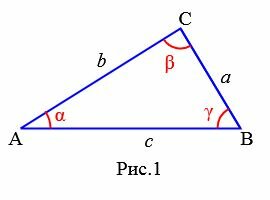Треугольник обозначается знаком ⊿. Например треугольник ABC обозначается так: ⊿ABC. Этот же треугольник можно обозначать так: ⊿BAC, ⊿CBA и т.д.

Углы треугольника обозначают так ∠BAC, ∠ABC, ∠BCA. Эти же углы коротко обозначают также ∠A, ∠B, ∠C, соответственно. Углы треугольника принято также обозначать греческими буквами α, β, γ и т.д. Стороны тркеугольника обозначают так AB, BC, AC. Принято также стороны обозначать одной строчной буквой, причем сторона напротив угла A ,обозначается буквой a, сторона напротив угла B− b, сторона напротив угла C− c. Сумма трех сторон треугольника называется периметром треугольника.

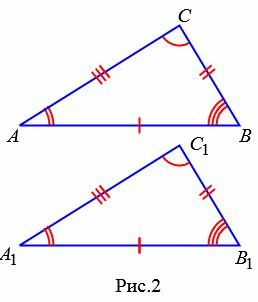
Как известно, две треугольники называются равными, если при наложении друг на друга их можно совместить. На Рис.2 представлены два треугольника ABC и A₁B₁C₁. Треугольник ABC можно наложить на треугольник A₁B₁C₁ так, чтобы вершины и стороны этих треугольников попарно совместились. Очевидно, что при этом совместятся и соответствующие углы.

Вышеизложенное можно сформулировать так:

Если два треугольника равны, то элементы (стороны и углы) одного треугольника соответственно равны элементам другого треугольника. Равенство треугольников ABC и A₁B₁C₁ обозначается так:

Видео:7 класс, 34 урок, Неравенство треугольникаСкачать

Первый признак равенства треугольников

Теорема 1. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то эти треугольники равны.

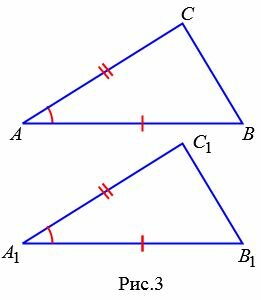Доказательство. Рассмотрим треугольники ABC и A₁B₁C₁ (Рис.3). Пусть AB=A₁B₁, AС=A₁С₁ и ∠A=∠A₁. Докажем, что .

Видео:Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Второй признак равенства треугольников

Теорема 2. Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то эти треугольники равны.

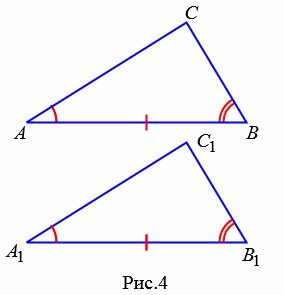Доказательство. Рассмотрим треугольники ABC и A₁B₁С₁ (Рис.4). Пусть AB=A₁B₁, ∠A=∠A₁, ∠B=∠B₁. Докажем, что .

Видео:Неравенства треугольника. 7 класс.Скачать

Третий признак равенства треугольников

Теорема 3. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то эти треугольники равны.

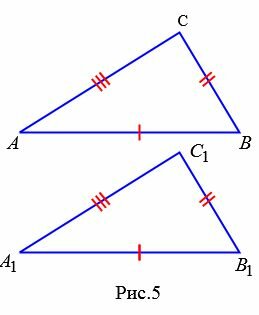Доказательство. Рассмотрим треугольники ABC и A₁B₁С₁. Пусть AB=A₁B₁, AC=A₁C₁ и BC=B₁C₁. Докажем, что . Приложим треугольник ABC к треугольнику A₁B₁С₁ так, чтобы вершина A совмещалась с вершиной A₁, вершина B совмещалась с вершиной B₁, а вершины С и С₁ находились по разные стороны от прямой A₁B₁.

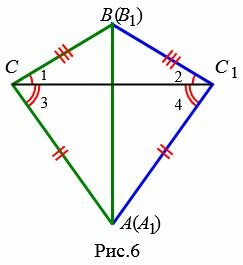Возможны три варианта: луч CC₁ проходит внутри угла ACB(Рис.6); луч CC₁ совпадает с одной из сторон угла ACB (Рис.7); луч CC₁ проходит вне угла ACB(Рис.8). Рассмотрим эти три случая по отдельности.

.

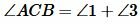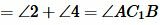Имеем AC=A₁C₁, BC=B₁C₁ ∠ACB=∠A₁C₁B₁ и по первому признаку равенства треугольников . Теорема доказана.

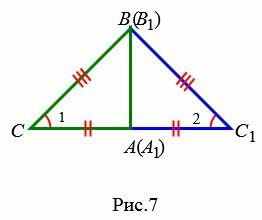Вариант 2 (Рис.7). Так как по условию теоремы AC=A₁C₁ и BC=B₁C₁, то треугольник BСС₁ равнобедренный. Тогда ∠1=∠2. Имеем: AC=A₁C₁, BC=B₁C₁, ∠1=∠2 и по первому признаку равенства треугольников . Теорема доказана.

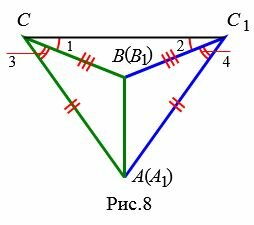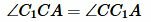
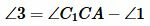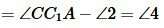Вариант 3 (Рис.8). Так как по условию теоремы AC=A₁C₁ и BC=B₁C₁, то треугольники AСС₁ и BСС₁ равнобедренные. Тогда ∠1=∠2 и и, следовательно:

.

Имеем AC=A₁C₁, BC=B₁C₁ 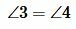и по первому признаку равенства треугольников . Теорема доказана.

Видео:Неравенства треугольника. Практическая часть. 7 класс.Скачать

Задачи и решения

Задача 1. На сторонах угла CAD отмечены точки B и E так, что точка B лежит на отрезке AC, а точка E − на отрезке AD, причем AC=AD и AB=AE. Докажите, что ∠CBD=∠DEC (Рис.9).

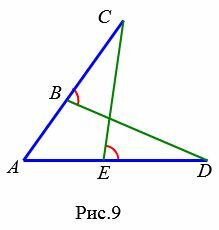Доказательство. AC=AD, AE=AB, ∠CAD общий для треугольников CAE и DAB. Тогда, по первому признаку равенства треугольников (теорема 1) ⊿ACE=⊿ADB. Следовательно ∠DBA=∠AEC. Поскольку углы CBD и DBA смежные, то CBD=180°−∠DBA. Аналогично CED=180°-∠AEC. То есть ∠CBD=∠DEC. Конец доказательства .

Задача 2. По данным рисунка рис.10 докажите, что OP=OT, ∠P=∠T

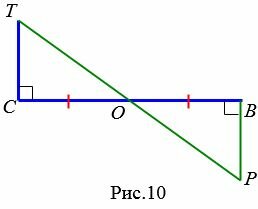Доказательство. OC=OB, ∠TCO=∠PBO=90°. Углы TOC и POB вертикальные (следовательно равны) тогда, повторому признаку равенства треугольников (теорема 2), ⊿TCO=⊿PBO. Конец доказательства .

Видео:✓ Неравенство треугольника | Ботай со мной #126 | Борис ТрушинСкачать

Урок геометрии в 7-м классе «Неравенство треугольника»

Разделы: Математика

Цель урока: изучить теорему о неравенстве треугольника и показать ее применение при решении задач.

Задачи:

• Образовательные:
  • относительно учащихся: научиться применять свойство «неравенство треугольника» и определять несуществующие треугольники;
  • относительно педагога: объяснить новую тему с первичным закреплением новых знаний; включить учеников в исследовательскую деятельность;
  • показать практическое применение полученных знаний; создать условия для формирования целостной картины мира.
• Развивающие:
  • развитие речи, мышления, сенсорной (восприятие внешнего мира через органы чувств) сферы личности и потребностно-мотивационной области;
  • развитие умственной деятельности (выполнять операции анализа, синтеза, способность наблюдать, делать выводы, выделять существенные признаки объектов, цели и способы деятельности, выдвигать гипотезы).
• Воспитательные:
  • повысить интерес к традициям края;
  • развивать самостоятельность, умение работать парами;
  • способствовать формированию коммуникативной компетенции.

Тип урока: урок изучения и первичного закрепления новых знаний.

Оборудование: доска, компьютер, интерактивная доска или мультимедийный проектор, презентация, учебники, рабочие тетради (Приложение 1), 14 наборов полосок из картона по 5 см, 7 см (2 шт.), 9 см, 12 см, 14 см, 16 см, таблички с треугольниками, смайлики (Приложение 2).

1. Организационный этап

2. Подготовка к основному этапу урока (обеспечение мотивации и принятия учащимися цели учебно-познавательной деятельности, актуализация опорных знаний)

– Посмотрите на рисунок, выполненный на доске. Как называется эта фигура? (Это треугольник.)
– Какая фигура называется треугольником? (Треугольник – фигура, состоящая из трех точек, не лежащих на одной прямой и трех отрезков, попарно соединяющих эти точки.)
– Что возникает в вашей памяти? Что вы можете рассказать об этом треугольнике? Если обозначить треугольник АВС, назовите большую сторону. (Ребята отвечают на вопросы учителя.)
– А почему именно эту фигуру я предложила вам вспомнить? (Будем изучать какие-то свойства треугольника.)
– Совершенно верно, сегодня мы будем изучать свойство «неравенство треугольника».

3.Усвоение новых знаний и способов действий

3.1. Постановка проблемы, выдвижение гипотезы

Еслиб только меня спросили,
Я б ответил предельно кратко,
Что не видел Земли красивей
И загадочней, чем Камчатка.

Где вулканы царапают небо,
Низвергая к подножьм лавы,
Где сплетаются быль и небыль,
И где в рост человека травы.

– Эти замечательные стихи Анатолия Старикана посвящены нашей малой родине Камчатке. Камчатка имеет свои традиции, и одной из них является ежегодное проведение Берингии.

– Ребята, а что такое Берингия? (Это ставшая традиционной гонка на собачьих упряжках, которая проводится с 1990 года.)

– Обычно Берингия проводится в марте и вместе с началом весны приходит в населенные пункты на своем пути, принося радость их обитателям. Стоит заметить, что гонка помимо состязательной составляющей, имеет еще и гуманитарное значение для жителей сел и поселков Камчатского края, где отдыхают участники гонки. Детям и школам отдаленных уголков Камчатки оказывают спонсорскую помощь.
В этом году Беригиня проходила с 7 по 21 марта.

Проблемная ситуация.

Берингия стартовала из села Эссо, и одним из пунктов остановки стал поселок Тигиль. Расстояние между этими населенными пунктами 443 км. Далее каюры отправились в поселок Оссора. На каком расстоянии от села Эссо может находиться поселок Оссора, если расстояние между поселком Тигиль и поселком Оссора 507 км?

Какую фигуру необходимо построить, чтобы решить эту проблему? (Необходимо построить треугольник.) Какова может быть длина третьей стороны? Выскажите свои гипотезы, мы проверим их в конце урока.
Ученики отвечают на вопросы учителя, строят треугольник в рабочей тетради и высказывают свои гипотезы, например, расстояние между с. Эссо и п. Оссора меньше 950 км.

1. 3.2. Проведение исследования, формулирование нового свойства сторон треугольника

Основной фигурой в рассматриваемой проблеме является треугольник. Я уверена, что вы очень наблюдательны. Скажите, а где еще в повседневной жизни вам встречались треугольные формы? В архитектуре? (Знак аварийной остановки и т.д. Крыши имеют треугольную форму.)
– Вы правы. Основу крыш составляют наклонные и горизонтальные балки, которые соединены между собой и образуют треугольник.
Давайте сконструируем макеты собственных крыш. Представьте, что те полоски, которые лежат перед вами – это балки для построения крыши дома.

Исследовательская работа

– Перед вами лежат макеты сторон треугольников.
Постройте, используя эти макеты треугольники со сторонами:

В первой задаче треугольник построить легко. Во второй получился отрезок. Почему? (Т.к. три вершины лежат на одной прямой, а треугольник – это фигура, составленная из трех точек, не лежащих на одной прямой, попарно соединенных отрезками. Длина большего отрезка равна сумме длин меньших.)

– Можно ли построить треугольник в третьем случае? (В третьем случае треугольник построить нельзя, так как длина большей стороны больше суммы длин меньших сторон.)

Учитель выслушивает версии учеников. В случае затруднения можно предложить детям сравнить длину стороны, построенной первой и сумму двух других сторон треугольника.

Верная версия детей: «Если сторона, построенная первой, меньше суммы двух других сторон, то треугольник строится».

– Итак, треугольник, с какими сторонами мы смогли построить? (Треугольник со сторонами 7, 12, 9.)

AB

5. Первичная проверка понимания и закрепление знаний

– Выберите, какие треугольники не существуют?

(Ученики работают самостоятельно, один человек работает у доски, потом проверка.)

Ответ: не существуют треугольники с номерами 3, 5, 6.

– Ребята, что вы заметили? Как быстро применить теорему о неравенстве треугольника?

(Высказывают свои версии.) – Сумма двух сторон, должна быть больше третьей стороны. Например, 10 + 3 > 5, но треугольник построить нельзя, почему? (Так как 3 + 5 18.04.2012

Видео:Неравенство треугольникаСкачать

Неравенство треугольника — определение и вычисление с примерами решения

Содержание:

Неравенство треугольника:

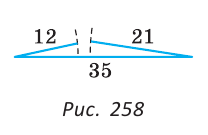
Опыт нам подсказывает, что путь из точки А в точку С по прямой АС короче, чем по ломаной ABC (рис. 255), т. е. АС 12+21 (рис. 258).

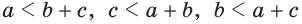
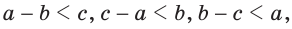
Замечание. Из неравенств треугольника следует, что то есть любая сторона треугольника больше разности двух других его сторон. Так, для стороны а справедливо

Пример:

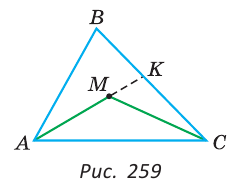
Внутри треугольника ABC взята точка М (рис. 259). Доказать, что периметр треугольника АМС меньше периметра треугольника ABC.

Решение:

Так как у треугольников ABC и АМС сторона АС — общая, то достаточно доказать, что AM + МС B (рис. 108, а).

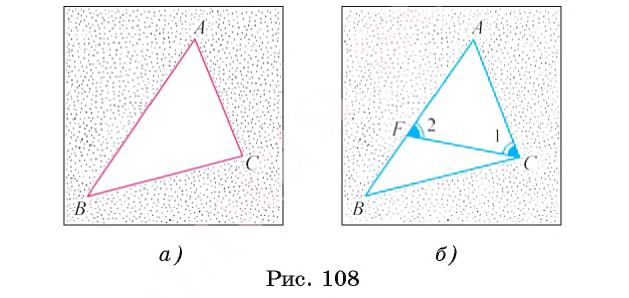
2) Отложим на стороне АВ отрезок АF, равный стороне AC (рис. 108, б).

3) Так как АF 1.

4) Угол 2 является внешним углом треугольника ВFС, следовательно, 2 > B.

5) Так как треугольник FАС является равнобедренным, то 1 = 2.

Таким образом, BСА > 1, 1 = 2 и 2 > B.

Отсюда получаем, что ВСА > B.

Теорема 2. В треугольнике против большего угла лежит большая сторона.

1) Пусть в треугольнике АBС С > B. Докажем, что АВ > АС (см. рис. 108, а). Доказательство проведем методом от противного.

2) Предположим, что это не так. Тогда: либо АВ = АС, либо АВ C.

В каждом из этих случаев получаем противоречие с условием: C > B. Таким образом, сделанное предположение неверно и, значит, АВ > АС.

Из данной теоремы следует утверждение: в прямоугольном треугольнике катет меньше гипотенузы.

Действительно, гипотенуза лежит против прямого угла, а катет — против острого. Поскольку прямой угол больше острого, то по теореме 2 получаем, что гипотенуза больше катета.

Теорема 3 (признак равнобедренного треугольника). Если два угла треугольника равны, то треугольник равнобедренный.

Пусть в треугольнике два угла равны. Тогда равны стороны, лежащие против этих углов. В самом деле, если предположить, что одна из указанных сторон больше другой, то по теореме 1 угол, лежащий против этой стороны, будет больше угла, лежащего против другой стороны, что противоречит условию равенства углов.

Значит, наше предположение неверно и в треугольнике две стороны равны, т. е. треугольник является равнобедренным.

Неравенство треугольника

Докажем, что длина каждой стороны треугольника меньше суммы длин двух других сторон.

Теорема 4. Длина каждой стороны треугольника меньше суммы длин двух других его сторон.

1) Пусть ABC — произвольный треугольник. Докажем, например, что выполняется неравенство АВ l, следовательно, верно неравенство АВF > 2.

4) Так как в треугольнике против большего угла лежит большая сторона (теорема 2), то АВ

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

📽️ Видео

Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Неравенство треугольника. Геометрия 7 класс. Доказательство. Задачи по рисункам.Скачать

ТРЕУГОЛЬНИКИ 1. Треугольник. Неравенство треугольника. Периметр треугольникаСкачать

Неравенство треугольникаСкачать

Геометрия 7 класс (Урок№24 - Соотношения между сторонами и углами треугольника. Неравенство треуг.)Скачать

Геометрия 7 класс. Треугольник. Определение, неравенство треугольника. Виды треугольников.Скачать

Периметр треугольника. Как найти периметр треугольника?Скачать

Неравенство треугольника, 7 класс, Математическая вертикальСкачать

Задание 25 Неравенство треугольникаСкачать

Задание 25 Неравенство треугольникаСкачать

ОГЭ Задание 25 Неравенство треугольникаСкачать

Неравенство треугольника ★ Любая сторона треугольника меньше суммы двух других сторонСкачать

Неравенство треугольника | Геометрия 7-9 класс #34 | ИнфоурокСкачать

Геометрия 7 класс | Математическая вертикаль | НЕРАВЕНАТВО РЕЗИНКИ | Неравенство треугольниковСкачать