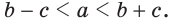Теорема 1 Любая сторона треугольника меньше суммы двух других сторон.
Доказательство. Рассмотрим произвольный треугольник ABC (Рис.1).
 |
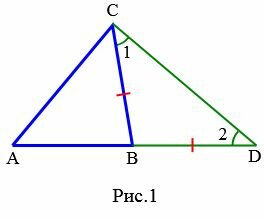Докажем, что ( small AC lt AB+BC .) На продолжении стороны AB отложим отрезок BD равный стороне BC. Полученный треугольник BCD равнобедренный. тогда ( small angle 1= angle 2.) Рассмотрим треугольник ADC. В этом треугольнике ( small angle ACD gt angle 1 ) и учитывая, что ( small angle 1= angle 2, ) получим ( small angle ACD gt angle 2. ) По теореме 1 статьи Соотношения между сторонами и углами треугольника, против большего угла треугольника лежит большая сторона. Следовательно в треугольнике ADC имеет место неравенство:
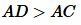 . | (1) |
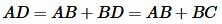 . | (2) |
Тогда из (1) и (2) получим:
  |
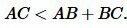Следствие 1. Для любых точек A, B, C, не расположенных на одной прямой справедливы следующие неравенства:
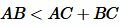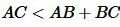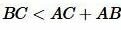 ,  ,  . | (3) |
Неравенства (3) называются неравенствами треугольника.
Видео:Неравенства треугольника. 7 класс.Скачать
Неравенство треугольника — определение и вычисление с примерами решения
Содержание:
Неравенство треугольника:
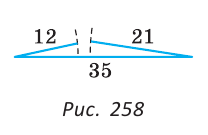
Опыт нам подсказывает, что путь из точки А в точку С по прямой АС короче, чем по ломаной ABC (рис. 255), т. е. АС 12+21 (рис. 258).
Замечание. Из неравенств треугольника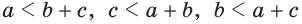 
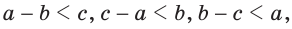
следует, что 
то есть любая сторона треугольника больше разности двух других его сторон. Так, для стороны а справедливо 
Пример:
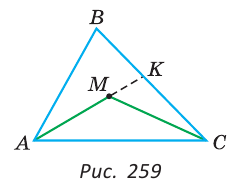
Внутри треугольника ABC взята точка М (рис. 259). Доказать, что периметр треугольника АМС меньше периметра треугольника ABC.
Решение:
Так как у треугольников ABC и АМС сторона АС — общая, то достаточно доказать, что AM + МС 
B (рис. 108, а).
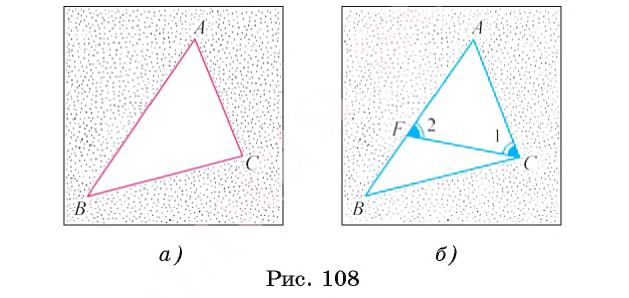
2) Отложим на стороне АВ отрезок АF, равный стороне AC (рис. 108, б).
3) Так как АF 1.
4) Угол 2 является внешним углом треугольника ВFС, следовательно, 2 > B.
5) Так как треугольник FАС является равнобедренным, то 1 = 2.
Таким образом, BСА > 1, 1 = 2 и 2 > B.
Отсюда получаем, что ВСА > B.
Теорема 2. В треугольнике против большего угла лежит большая сторона.
1) Пусть в треугольнике АBС С > B. Докажем, что АВ > АС (см. рис. 108, а). Доказательство проведем методом от противного.
2) Предположим, что это не так. Тогда: либо АВ = АС, либо АВ C.
В каждом из этих случаев получаем противоречие с условием: C > B. Таким образом, сделанное предположение неверно и, значит, АВ > АС.
Из данной теоремы следует утверждение: в прямоугольном треугольнике катет меньше гипотенузы.
Действительно, гипотенуза лежит против прямого угла, а катет — против острого. Поскольку прямой угол больше острого, то по теореме 2 получаем, что гипотенуза больше катета.
Теорема 3 (признак равнобедренного треугольника). Если два угла треугольника равны, то треугольник равнобедренный.
Пусть в треугольнике два угла равны. Тогда равны стороны, лежащие против этих углов. В самом деле, если предположить, что одна из указанных сторон больше другой, то по теореме 1 угол, лежащий против этой стороны, будет больше угла, лежащего против другой стороны, что противоречит условию равенства углов.
Значит, наше предположение неверно и в треугольнике две стороны равны, т. е. треугольник является равнобедренным.
Неравенство треугольника
Докажем, что длина каждой стороны треугольника меньше суммы длин двух других сторон.
Теорема 4. Длина каждой стороны треугольника меньше суммы длин двух других его сторон.
1) Пусть ABC — произвольный треугольник. Докажем, например, что выполняется неравенство АВ l, следовательно, верно неравенство АВF > 2.
4) Так как в треугольнике против большего угла лежит большая сторона (теорема 2), то АВ
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать
Неравенство треугольника: доказательство, примеры, решенные упражнения
Неравенство треугольника: доказательство, примеры, решенные упражнения — Наука
Видео:✓ Неравенство треугольника | Ботай со мной #126 | Борис ТрушинСкачать
Содержание:
Это называется неравенство треугольника к свойству двух действительных чисел, заключающемуся в том, что абсолютное значение их суммы всегда меньше или равно сумме их абсолютных значений. Это свойство также известно как неравенство Минковского или треугольное неравенство.
Это свойство чисел называется треугольным неравенством, потому что в треугольниках длина одной стороны всегда меньше или равна сумме двух других, даже если это неравенство не всегда применяется в области треугольников.
Существует несколько доказательств треугольного неравенства в действительных числах, но в этом случае мы выберем одно, основанное на свойствах абсолютного значения и биномиального квадрата.
Теорема: Для каждой пары чисел к Y б относящиеся к действительным числам, он должен:
Видео:Первый признак равенства треугольников. 7 класс.Скачать
Демонстрация
Начнем с рассмотрения первого члена неравенства, который возведем в квадрат:
| a + b | ^ 2 = (a + b) ^ 2 = a ^ 2 + 2 a b + b ^ 2 (уравнение 1)
На предыдущем шаге мы использовали свойство, согласно которому любое число в квадрате равно абсолютному значению указанного числа в квадрате, то есть:| х | ^ 2 = х ^ 2. Также использовалось квадратное биномиальное разложение.
Все номера Икс меньше или равно его абсолютному значению. Если число положительное, оно равно, но если число отрицательное, оно всегда будет меньше положительного числа. В этом случае его собственное абсолютное значение, то есть можно сказать, что x ≤ | х |.
Продукт (а б) является числом, поэтому применяется, что (а б) ≤ | а б |. Когда это свойство применяется к (уравнение 1), мы имеем:
| a + b | ^ 2 = a ^ 2 + 2 (a b) + b ^ 2 ≤ a ^ 2 + 2 | а б | + b ^ 2 (уравнение 2)
Учитывая, что | a b | = | а || б | la (уравнение 2) можно записать следующим образом:
| a + b | ^ 2 ≤ a ^ 2 + 2 | а || б | + b ^ 2 (уравнение 3)
Но поскольку мы говорили ранее, что квадрат числа равен абсолютному значению квадрата числа, то уравнение 3 можно переписать следующим образом:
| a + b | ^ 2 ≤ | a | ^ 2 + 2 | a | | б | + | b | ^ 2 (уравнение 4)
Во втором члене неравенства признается замечательный продукт, применение которого приводит к:
| a + b | ^ 2 ≤ (| a | + | b |) ^ 2 (уравнение 5)
В предыдущем выражении следует отметить, что значения, которые должны быть возведены в квадрат в обоих членах неравенства, положительны, поэтому необходимо также убедиться, что:
| а + б | ≤ (| a | + | b |) (уравнение 6)
Вышеприведенное выражениеэто именно то, что хотели продемонстрировать.
Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать
Примеры
Далее мы проверим треугольное неравенство на нескольких примерах.
Видео:Признаки равенства треугольников. 7 класс.Скачать
Пример 1
Мы берем значение a = 2 и значение b = 5, то есть оба положительных числа, и проверяем, выполняется ли неравенство.
Равенство проверено, следовательно, теорема о неравенстве треугольника выполнена.
Видео:7 класс, 15 урок, Первый признак равенства треугольниковСкачать
Пример 2
Выбираются следующие значения a = 2 и b = -5, то есть положительное число, а другое отрицательное, проверяем, выполняется неравенство или нет.
Неравенство выполнено, следовательно, теорема о треугольном неравенстве проверена.
Видео:7 класс, 34 урок, Неравенство треугольникаСкачать
Пример 3
Берём значение a = -2 и значение b = 5, то есть отрицательное число, а другое положительное, проверяем, выполняется ли неравенство.
Неравенство проверено, значит, теорема выполнена.
Видео:Геометрия 7 класс (Урок№10 - Первый признак равенства треугольников.)Скачать
Пример 4
Выбираются следующие значения a = -2 и b = -5, то есть оба отрицательные числа, и мы проверяем, выполняется неравенство или нет.
Равенство проверено, следовательно, теорема о неравенстве Минковского выполнена.
Видео:Задачи на доказательство по геометрии. Первый признак равенства треугольников.Скачать
Пример 5
Мы берем значение a = 0 и значение b = 5, то есть число ноль, а другое положительное, затем проверяем, выполняется неравенство или нет.
Равенство выполнено, следовательно, теорема о неравенстве треугольника проверена.
Видео:Неравенство треугольника. Геометрия 7 класс. Доказательство. Задачи по рисункам.Скачать
Пример 6
Мы берем значение a = 0 и значение b = -7, то есть число ноль, а другое положительное, затем проверяем, выполняется неравенство или нет.
Равенство проверено, следовательно, теорема о треугольном неравенстве выполнена.
Видео:Неравенство треугольникаСкачать
Решенные упражнения
В следующих упражнениях изобразите геометрически неравенство треугольника или неравенство Минковского для чисел a и b.
Число a будет представлено как сегмент на оси X, его начало O совпадает с нулем оси X, а другой конец сегмента (в точке P) будет в положительном направлении (вправо) от оси X, если > 0, но если a 0), а точка Q будет | b | единиц слева от P, если b Предыдущая статья
Херман Дехеса: биография, стиль и творчество
Богомол: характеристика, среда обитания, размножение, кормление
💡 Видео
Неравенство треугольника ★ Любая сторона треугольника меньше суммы двух других сторонСкачать
Геометрия 7 класс (Урок№15 - Решение задач на признаки равенства треугольников.)Скачать
7 класс, 36 урок, Признаки равенства прямоугольных треугольниковСкачать
Задачи на доказательство равенства треугольников. Первый признак. Простые.Скачать
Признаки равенства треугольников. Практическая часть. 7 класс.Скачать
Неравенство Коши — Буняковского | Ботай со мной #049 | Борис Трушин |Скачать
Геометрия 7 класс (Урок№14 - Второй и третий признаки равенства треугольников.)Скачать
Первый признак равенства треугольников | Теорема + доказательствоСкачать
