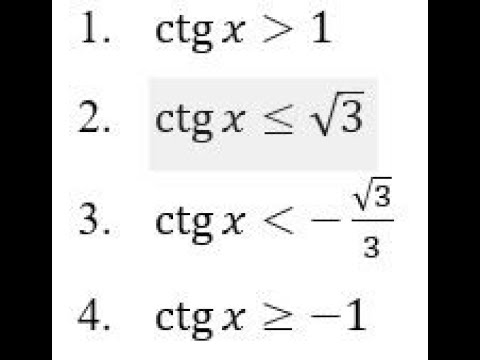Неравенства с тангенсом и котангенсом с помощью окружности (4 видео)

Простейшие тригонометрические неравенства

Содержание

п.1. Решение неравенств с синусом
п.2. Решение неравенств с косинусом
п.3. Решение неравенств с тангенсом
п.4. Решение неравенств с котангенсом
п.5. Примеры
Простейшие и сложные тригонометрические неравенства
Простейшие тригонометрические неравенства
Способ 1 – Решение неравенств с помощью построения графика функции
Способ 2 – Решение тригонометрических неравенств с помощью единичной окружности
Сложные тригонометрические неравенства
Простейшие тригонометрические уравнения (задание 5) и неравенства
📸 Видео

п.1. Решение неравенств с синусом

Алгоритм решения неравенства (sinxgt a)

Шаг 1. В числовой окружности на оси синусов отметить точку с ординатой (a). Провести горизонталь (y=a), отметить точки её пересечения с окружностью.

Шаг 2. Решить уравнение (sin⁡x=a). Про решение простейших тригонометрических уравнений – см. §19 данного справочника. Полученные базовые решения являются значениями точек пересечения, подписать их.

Шаг 3. Дуга числовой окружности над проведенной горизонталью – искомое решение. Записать ответ, обходя дугу против часовой стрелки. Добавить к концам полученного интервала полный период.
Решение имеет вид: ((arcsina+2pi k; pi-arcsin a+2pi k))

Неравенства с тангенсом и котангенсом с помощью окружности

$$ sin xgt frac12 $$ 1. Проводим горизонталь (y=frac12), отмечаем точки пересечения (незакрашенные, т.к. неравенство строгое).
2. Решаем уравнение (sinx=frac12) begin x=(-1)^kfracpi6+pi k= left[ begin fracpi6+2pi k\ frac+2pi k end right. end Подписываем точку справа (fracpi6) и точку слева (frac).
3. При обходе полученной дуги против часовой стрелки получаем интервал: ((fracpi6; frac)). Добавляем к концам интервала полный период.
Ответ: (left(fracpi6;+2pi k; frac+2pi kright))

Алгоритм решения неравенства (sinxgeq a) будет таким же, только точки на числовой окружности будут закрашенными, и в ответе будет отрезок (с квадратными скобками).

Алгоритм решения неравенства (sin⁡xlt a) будет отличаться тем, что в ответе нужно записывать дугу под горизонталью (y=a). При этом не забываем, что дугу нужно обходить в сторону возрастания. Поэтому угол слева пишут отрицательным (отсчитывая период назад).

Наконец, в неравенстве (sin⁡xleq a) всё будет то же, что и в (sin⁡xlt a). Только точки на концах будут закрашенными и войдут в ответ (с квадратными скобками).

$$ sin xleq -frac<sqrt> $$ 1. Проводим горизонталь (y=-frac<sqrt>), отмечаем точки пересечения (закрашенные, т.к. неравенство нестрогое).
2. Решаем уравнение (sinx=-frac<sqrt>) begin x=(-1)^kleft(-fracpi4right)+pi k= left[ begin -frac+2pi k\ -frac+2pi k end right. end Подписываем точку справа (-frac) и точку слева (-frac).
3. При обходе полученной дуги против часовой стрелки получаем отрезок: (left[-frac;-fracright]). Добавляем к концам отрезка полный период.
Ответ: (left[-frac+2pi k;-frac+2pi kright])

п.2. Решение неравенств с косинусом

Алгоритм решения неравенства (cosxgt a)

Шаг 1. В числовой окружности на оси косинусов отметить точку с абсциссой (a). Провести вертикаль (x=a), отметить точки её пересечения с окружностью.

Шаг 2. Решить уравнение (cos⁡x=a). Полученные базовые решения являются значениями точек пересечения, подписать их.

Шаг 3. Дуга числовой окружности справа от проведенной вертикали – искомое решение. Записать ответ, обходя дугу против часовой стрелки. Добавить к концам полученного интервала полный период.
Решение имеет вид: ((-arccos⁡a+2pi k; arccos⁡a+2pi k))

$$ cosxgt frac<sqrt> $$ 1. Проводим вертикаль (x=frac<sqrt>), отмечаем точки пересечения (незакрашенные, т.к. неравенство строгое).
2. Решаем уравнение (cosx=frac<sqrt>) begin x=pmfracpi6+2pi k end Подписываем точку снизу (-fracpi6) и точку сверху (frac).
3. При обходе полученной дуги против часовой стрелки получаем интервал: (left(-fracpi6;fracpi6right)). Добавляем к концам интервала полный период.
Ответ: (left(-fracpi6;+2pi k; frac+2pi kright))

Алгоритм решения неравенства (cosxgeq a) будет таким же, только точки на числовой окружности будут закрашенными, и в ответе будет отрезок (с квадратными скобками).

Алгоритм решения неравенства (cosxlt a) будет отличаться тем, что в ответе нужно записывать дугу слева от вертикали (x=a). При этом не забываем, что дугу нужно обходить в сторону возрастания, сверху вниз. Значение угла снизу должно быть больше, чем угла сверху.

Наконец, в неравенстве (cos⁡xleq a) всё будет то же, что и в (cosxlt a). Только точки на концах будут закрашенными и войдут в ответ (с квадратными скобками).

п.3. Решение неравенств с тангенсом

Алгоритм решения неравенства (tgxgt a)

Шаг 1. На оси тангенсов (касательной к числовой окружности в точке (1,0)) отметить точку с ординатой (a). Провести луч из начала координат через отмеченную точку, отметить точку её пересечения с окружностью.

Шаг 2. Решить уравнение (tg⁡x=a). Полученное базовое решение является значением точки пересечения.

Шаг 3. Дуга числовой окружности от отмеченной точки до (fracpi2) (в которой (tgxrightarrow +infty)) – искомое решение. Записать ответ, обходя дугу против часовой стрелки. Добавить к концам полученного интервала полный период.
Решение имеет вид: (left(arctga+pi k; fracpi2+pi kright))

$$ tg xgt -frac<sqrt> $$ 1. На оси тангенсов отмечаем точку (-frac<sqrt>). Проводим луч из начала координат через эту точку.
2. Решаем уравнение (tgx=-frac<sqrt>) begin x=-fracpi6+pi k end Подписываем точку снизу (-fracpi6.) Верхней границей интервала будет (fracpi2), угол, в котором (tgxrightarrow +infty .)
3. При обходе полученной дуги против часовой стрелки получаем интервал: (left(-fracpi6;fracpi2right)). Добавляем к концам интервала период для тангенса.
Строго говоря, на числовой окружности длиной (2pi) получим две дуги для тангенса с периодом (pi). Ответ: (left(-fracpi6;+pi k; frac+pi kright))

Алгоритм решения неравенства (tg⁡xlt a) будет отличаться тем, что в ответе нужно записывать дугу от точки (-fracpi2) (в которой (tgxrightarrow -infty)) до найденного арктангенса.

Для нестрогих неравенств будут получаться полуинтервалы, в которых точки (pmfracpi2) ((tgxrightarrow pminfty)) будут ограничены круглой скобкой, а найденные арктангенсы – квадратной.

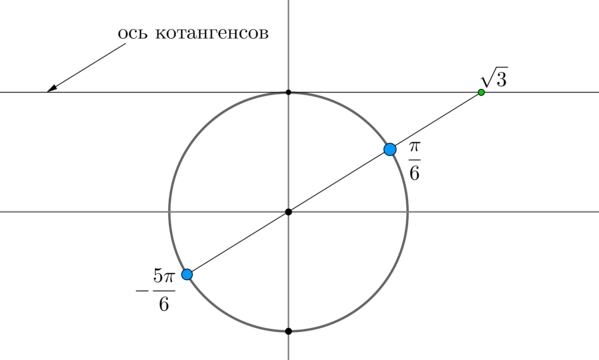
п.4. Решение неравенств с котангенсом

Решение неравенств с котангенсом аналогично решению с тангенсом. Для решения используется ось котангенсов (касательная к числовой окружности в точке (0;1)).

В неравенствах вида (ctgxgt a) пределу (ctgxrightarrow +infty) соответствует угол 0.

В неравенствах вида (ctgxlt a) пределу (ctgxrightarrow -infty) соответствует угол (pi).

п.5. Примеры

Пример 1. Решите неравенства:

a) (sinxleq frac<sqrt>) $$ xinleft[-frac+2pi k; frac+2pi kright] $$	б) (cosxlt -frac) $$ xinleft(frac+2pi k; frac+2pi kright) $$
в) (sinxgt -frac<sqrt>) $$ xinleft(-frac+2pi k; frac+2pi kright] $$	г) (tgxgeq 1) $$ xinleft.left(-frac+pi k; frac+pi kright.right] $$

Пример 2*. Решите неравенства:

a) (cosxgt -1)
Справа от вертикали (x=-1) расположена вся числовая окружность, кроме точки (pi).

Ответ: (xne pi+2pi k)б) (4cos^2frac x2-3leq 0)
(4cdot fracleq 3)
(2+2cosxleq 3)
(cosxleqfrac12)

Ответ: (left[fracpi3+2pi k; frac+2pi kright])

в) (-sqrtlt tgxleq 5)
(-arctgsqrt+pi klt xleq arctg5+pi k)
(-fracpi3+pi klt xleq arctg5+pi k)
Ответ: (left.left(-frac+pi k; arctg5+pi kright.right])

г) (tgleft(x-fracpi4right)gtsqrt)
(arctgsqrt+pi klt x-fracpi4ltfracpi2+pi k)
(fracpi4+fracpi3+pi klt xltfracpi4+fracpi2+pi k)
(frac+pi klt xltfrac+pi k)
Ответ: (left(frac+pi k; frac+pi kright))

Видео:10 класс, 22 урок, Простейшие тригонометрические уравнения неравенстваСкачать

Простейшие и сложные тригонометрические неравенства

Неравенства – это соотношения вида a › b, где a и b – есть выражения, содержащие как минимум одну переменную. Неравенства могут быть строгими – ‹, › и нестрогими – ≥, ≤.

Тригонометрические неравенства представляют собой выражения вида: F(x) › a, F(x) ‹ a, F(x) ≤ a, F(x) ≥ a, в которых F(x) представлено одной или несколькими тригонометрическими функциями.

Видео:Решение тригонометрических неравенств. 10 класс.Скачать

Простейшие тригонометрические неравенства

Примером простейшего тригонометрического неравенства является: sin x ‹ 1/2. Решать подобные задачи принято графически, для этого разработаны два способа.

Способ 1 – Решение неравенств с помощью построения графика функции

Чтобы найти промежуток, удовлетворяющий условиям неравенство sin x ‹ 1/2, необходимо выполнить следующие действия:

На координатной оси построить синусоиду y = sin x.
На той же оси начертить график числового аргумента неравенства, т. е. прямую, проходящую через точку ½ ординаты ОY.
Отметить точки пересечения двух графиков.
Заштриховать отрезок являющийся, решением примера.

Когда в выражении присутствуют строгие знаки, точки пересечения не являются решениями. Так как наименьший положительный период синусоиды равен 2π, то запишем ответ следующим образом:

Если знаки выражения нестрогие, то интервал решений необходимо заключить в квадратные скобки – [ ]. Ответ задачи можно также записать в виде очередного неравенства:

Способ 2 – Решение тригонометрических неравенств с помощью единичной окружности

Подобные задачи легко решаются и с помощью тригонометрического круга. Алгоритм поиска ответов очень прост:

Сначала стоит начертить единичную окружность.
Затем нужно отметить значение аркфункции аргумента правой части неравенства на дуге круга.
Нужно провести прямую проходящую через значение аркфункции параллельно оси абсциссы (ОХ).
После останется только выделить дугу окружности, являющуюся множеством решений тригонометрического неравенства.
Записать ответ в требуемой форме.

Разберем этапы решения на примере неравенства sin x › 1/2. На круге отмечены точки α и β – значения

Точки дуги, расположенные выше α и β, являются интервалом решения заданного неравенства.

Если нужно решить пример для cos, то дуга ответов будет располагаться симметрично оси OX, а не OY. Рассмотреть разницу между интервалами решений для sin и cos можно на схемах приведенных ниже по тексту.

Графические решения для неравенств тангенса и котангенса будут отличаться и от синуса, и от косинуса. Это обусловлено свойствами функций.

Арктангенс и арккотангенс представляют собой касательные к тригонометрической окружности, а минимальный положительный период для обеих функций равняется π. Чтобы быстро и правильно пользоваться вторым способом, нужно запомнить на какой из оси откладываются значения sin, cos, tg и ctg.

Касательная тангенс проходит параллельно оси OY. Если отложить значение arctg a на единичном круге, то вторая требуемая точка будет расположено в диагональной четверти. Углы

являются точками разрыва для функции, так как график стремится к ним, но никогда не достигает.

В случае с котангенсом касательная проходит параллельно оси OX, а функция прерывается в точках π и 2π.

Видео:Как решать тригонометрические неравенства?Скачать

Сложные тригонометрические неравенства

Если аргумент функции неравенства представлен не просто переменной, а целым выражением содержащим неизвестную, то речь уже идет о сложном неравенстве. Ход и порядок его решения несколько отличаются от способов описанных выше. Допустим необходимо найти решение следующего неравенства:

Графическое решение предусматривает построение обычной синусоиды y = sin x по произвольно выбранным значениям x. Рассчитаем таблицу с координатами для опорных точек графика:

В результате должна получиться красивая кривая.

Для простоты поиска решения заменим сложный аргумент функции

Пересечение двух графиков позволяет определить область искомых значений, при которых выполняется условие неравенства.

Найденный отрезок является решением для переменной t:

Однако, цель задания найти все возможные варианты неизвестной x:

Решить двойное неравенство достаточно просто, нужно перенести π/3 в крайние части уравнения и произвести требуемые вычисления:

Ответ на задание будет выглядеть как интервал для строгого неравенства:

Подобные задачи потребует опыта и сноровки учащихся в обращении с тригонометрическими функциями. Чем больше тренировочных заданий будет решено в процессе подготовке, тем проще и быстрее школьник найдет ответ на вопрос ЕГЭ теста.

Видео:ТРИГОНОМЕТРИЧЕСКИЕ НЕРАВЕНСТВА 10 класс тригонометрияСкачать

Простейшие тригонометрические уравнения (задание 5) и неравенства

(blacktriangleright) Стандартные (простейшие) тригонометричекие уравнения — это уравнения вида
(sin x=a,quad cos x=a,quad mathrm,x=b,quad mathrm,x=b) , которые имеют смысл при (-1leq aleq 1,quad bin mathbb) .

Для решения данных уравнения удобно пользоваться единичной окружностью (радиус равен (1) ).

Рассмотрим несколько примеров:

Пример 1. Решить уравнение (sin x=dfrac12) .

Найдем на оси синусов точку (dfrac12) и проведем прямую параллельно оси (Ox) до пересечения с окружностью. Получим две точки на окружности, в которых находятся все углы, синус которых равен (dfrac12) . Выберем в каждой точке по одному углу, причем удобнее выбирать эти углы из отрезка ([-pi;pi]) . Тогда в нашем случае это углы (dfrac6) и (dfrac6) . Все остальные углы можно получить путем прибавления к данным углам (2picdot n) , где (n) — целое число (т.е. поворотом от данных на целое число полных кругов).

Таким образом, решением являются (x_1=dfrac6+2pi n, x_2=dfrac6+2pi n, nin mathbb) .

Пример 2. Решить уравнение (cos x=-dfrac) .

Найдем на оси косинусов точку (-dfrac) и проведем прямую параллельно оси (Oy) до пересечения с окружностью. Получим две точки на окружности, в которых находятся все углы, косинус которых равен (-dfrac) . Выберем в каждой точке по одному углу, причем удобнее выбирать эти углы из отрезка ([-pi;pi]) . Тогда в нашем случае это углы (dfrac4) и (-dfrac4) . Все остальные углы можно получить путем прибавления к данным (2picdot n) , где (n) — целое число.

Таким образом, решением являются (x_1=dfrac4+2pi n, x_2=-dfrac4+2pi n, nin mathbb) .

Пример 3. Решить уравнение (mathrm,x=dfrac3) .

Найдем на оси тангенсов точку (dfrac3) и проведем прямую через эту точку и центр окружности до пересечения с окружностью. Получим две точки на окружности, в которых находятся все углы, тангенс которых равен (dfrac3) .Выберем в каждой точке по одному углу, причем удобнее выбирать эти углы из отрезка ([-pi;pi]) . Тогда в нашем случае это углы (dfrac6) и (-dfrac6) . Все остальные углы можно получить путем прибавления к данным (2picdot n) , где (n) — целое число, или путем прибавления к одному из данных углов (pi n) .

Таким образом, решением являются (x=dfrac6+pi n, nin mathbb) .

Пример 4. Решить уравнение (mathrm,x=sqrt3) .

Найдем на оси котангенсов точку (sqrt3) и проведем прямую через эту точку и центр окружности до пересечения с окружностью. Получим две точки на окружности, в которых находятся все углы, котангенс которых равен (sqrt3) . Выберем в каждой точке по одному углу, причем удобнее выбирать эти углы из отрезка ([-pi;pi]) . Тогда в нашем случае это углы (dfrac6) и (-dfrac6) . Все остальные углы можно получить путем прибавления к данным (2picdot n) , где (n) — целое число, или путем прибавления к одному из данных углов (pi n) .

Таким образом, решением являются (x=dfrac6+pi n, nin mathbb) .

(blacktriangleright) Решения для любого стандартного тригонометрического уравнения выглядят следующим образом: [begin hline text & text & text\ hline &&\ sin x=a & -1leq aleq 1 & left[ begin begin &x=arcsin a+2pi n\ &x=pi -arcsin a+2pi n end end right. , nin mathbb\&&\ hline &&\ cos x=a & -1leq aleq 1 & x=pm arccos a+2pi n, nin mathbb\&&\ hline &&\ mathrm, x=b & bin mathbb & x=mathrm, b+pi n, nin mathbb\&&\ hline &&\ mathrm,x=b & bin mathbb & x=mathrm, b+pi n, nin mathbb\&&\ hline end] Иногда для более короткой записи решение для (sin x=a) записывают как (x=(-1)^kcdot arcsin a+pi k, kin mathbb) .

(blacktriangleright) Любые уравнения вида (mathrm,big(f(x)big)=a) , (где (mathrm) — одна из функций (sin, cos, mathrm, mathrm) , а аргумент (f(x)) — некоторая функция) сводятся к стандартным уравнениям путем замены (t=f(x)) .

Пример 5. Решить уравнение (sin<(pi x+dfrac3)>=1) .

Сделав замену (t=pi x+dfrac3) , мы сведем уравнение к виду (sin t=1) . Решением данного уравнения являются (t=dfrac2+2pi n, ninmathbb) .

Теперь сделаем обратную замену и получим: (pi x+dfrac3=dfrac2+2pi n) , откуда (x=dfrac16+2n, ninmathbb) .

Если (n) точек, являющихся решением уравнения или системы, разбивают окружность на (n) равных частей, то их можно объединить в одну формулу: (x=alpha+dfracn, ninmathbb) , где (alpha) — один из этих углов.

Рассмотрим данную ситуацию на примере:

Пример 6. Допустим, решением системы являются (x_1=pm dfrac4+2pi n, x_2=pm dfrac4+2pi n, ninmathbb) . Отметим эти точки на окружности:

Заметим, что длины дуг (buildrelsmileover, buildrelsmileover, buildrelsmileover, buildrelsmileover) равны (dfrac2) , то есть эти точки разбили окружность на (4) равных части. Таким образом, ответ можно записать в виде одной формулы: (x=dfrac4+dfrac2n, ninmathbb) .

где (lor) — один из знаков (leq, , geq) .

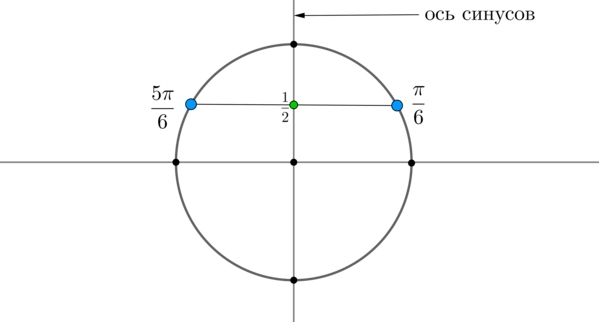
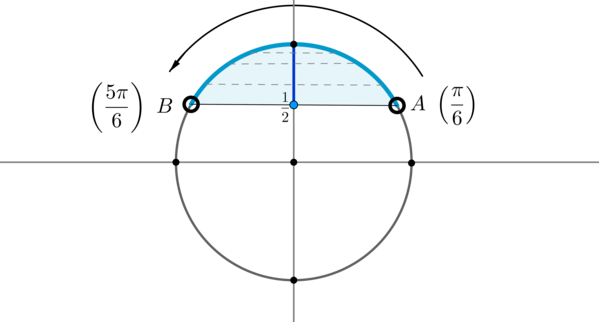
Пример 7. Изобразить на окружности множество решений неравенства (sin x >dfrac12) .

Для начала отметим на окружности корни уравнения (sin x =dfrac12) . Это точки (A) и (B) . Все точки, синус которых больше (dfrac12) , находятся на выделенной дуге. Т.к. при положительном обходе движение по окружности происходит против часовой стрелки, то начало дуги — это (A) , а конец — (B) .

Выберем в точке (A) любой угол, например, (dfrac6) . Тогда в точке (B) необходимо выбрать угол, который будет больше (dfrac6) , но ближайший к нему, и чтобы синус этого угла также был равен (dfrac12) . Это угол (dfrac6) . Тогда все числа из промежутка (left(dfrac6;dfrac6right)) являются решениями данного неравенства (назовем такое решение частным). А все решения данного неравенства будут иметь вид (left(dfrac6+2pi n;dfrac6+2pi nright), ninmathbb) , т.к. у синуса период (2pi) .

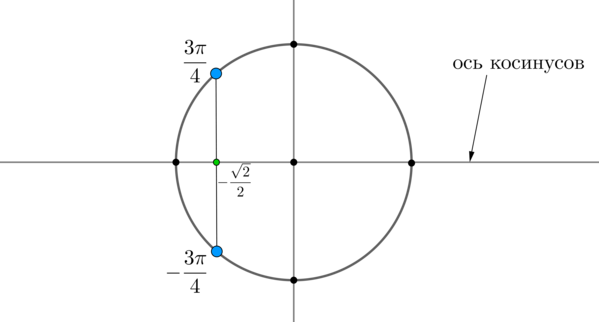
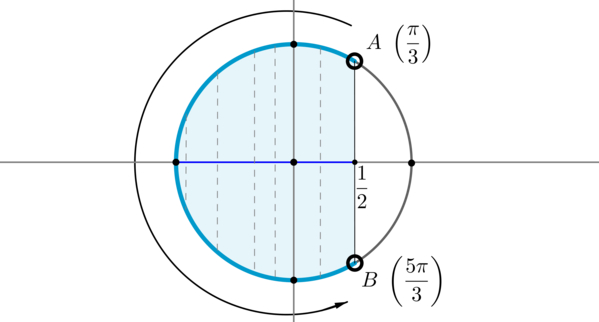
Пример 8. Изобразить на окружности множество решений неравенства (cos x .

Для начала отметим на окружности корни уравнения (cos x =dfrac12) . Это точки (A) и (B) . Все точки, косинус которых меньше (dfrac12) , находятся на выделенной дуге. Т.к. при положительном обходе движение по окружности происходит против часовой стрелки, то начало дуги — это (A) , а конец — (B) .

Выберем в точке (A) любой угол, например, (dfrac3) . Тогда в точке (B) необходимо выбрать угол, который будет больше (dfrac3) , но ближайший к нему, и чтобы косинус этого угла также был равен (dfrac12) . Это угол (dfrac3) . Тогда все числа из промежутка (left(dfrac3;dfrac3right)) являются решениями данного неравенства (назовем такое решение частным). А все решения данного неравенства будут иметь вид (left(-dfrac3+2pi n;-dfrac3+2pi nright), ninmathbb) , т.к. у косинуса период (2pi) .

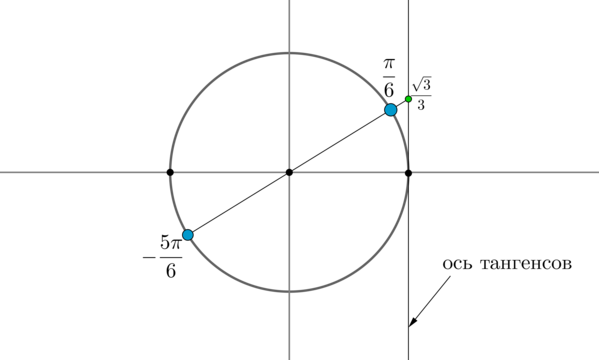
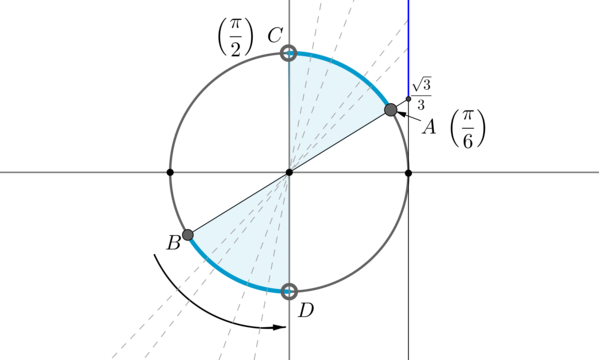
Пример 9. Изобразить на окружности множество решений неравенства (mathrm, x geq dfrac<sqrt>3) .

Для начала отметим на окружности корни уравнения (mathrm, x = dfrac<sqrt>3) . Это точки (A) и (B) . Все точки, тангенс которых больше или равен (dfrac<sqrt>3) , находятся на выделенных дугах, причем точки (C) и (D) выколоты, т.к. в них тангенс не определен.

Рассмотрим одну из дуг, например, (buildrelsmileover) . Т.к. при положительном обходе движение по окружности происходит против часовой стрелки, то за конец дуги можно принять угол (dfrac2) , тогда начало дуги — это угол (dfrac6) (угол должен быть меньше (dfrac2) , но ближайший к нему). Значит, частным решением данного неравенства является полуинтервал (Big[dfrac6;dfrac2Big)) . А все решения данного неравенства будут иметь вид (Big[dfrac6+pi n;dfrac2+pi nBig), ninmathbb) , т.к. у тангенса период (pi) .

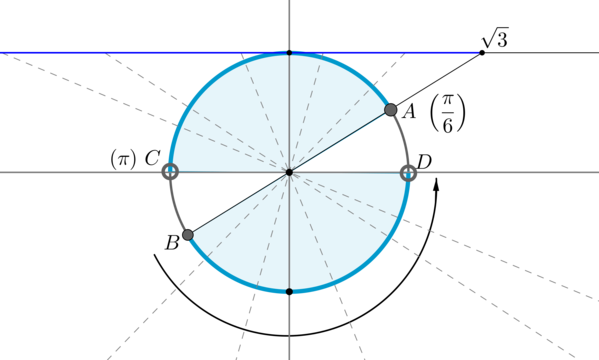
Пример 10. Изобразить на окружности множество решений неравенства (mathrm, x leq sqrt) .

Для начала отметим на окружности корни уравнения (mathrm, x = sqrt) . Это точки (A) и (B) . Все точки, котангенс которых меньше или равен (sqrt) , находятся на выделенных дугах, причем точки (C) и (D) выколоты, т.к. в них котангенс не определен.

Рассмотрим одну из дуг, например, (buildrelsmileover) . Т.к. при положительном обходе движение по окружности происходит против часовой стрелки, то за конец дуги можно принять угол (pi) , тогда начало дуги — это угол (dfrac6) (угол должен быть меньше (pi) , но ближайший к нему). Значит, частным решением данного неравенства является полуинтервал (Big[dfrac6;piBig)) . А все решения данного неравенства будут иметь вид (Big[dfrac6+pi n;pi+pi nBig), ninmathbb) , т.к. период котангенса (pi) .

Геометрический способ (по окружности).
Этот способ заключается в том, что мы отмечаем решения всех уравнений (неравенств) на единичной окружности и пересекаем (объединяем) их.

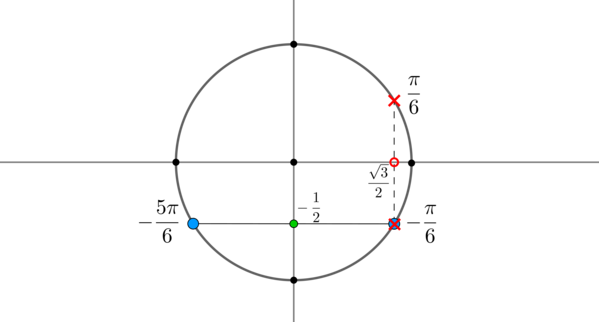
Пример 11. Найти корни уравнения (sin x=-dfrac12) , если (cos xne dfrac2) .

В данном случае необходимо пересечь решения первого уравнения с решением второго уравнения.

Решением первого уравнения являются (x_1=-dfrac6+2pi n, x_2=-dfrac6+2pi n, nin mathbb) , решением второго являются (xne pm dfrac6+2pi n, ninmathbb) . Отметим эти точки на окружности:

Видим, что из двух точек, удовлетворяющих первому уравнению, одна точка (x= -dfrac6+2pi n) не подходит. Следовательно, ответом будут только (x=-dfrac6+2pi n, nin mathbb) .

Вычислительный способ.
Этот способ заключается в подстановке решений уравнения (системы) в имеющиеся ограничения. Для данного способа будут полезны некоторые частные случаи формул приведения: [begin &sin=begin sin alpha, text n — text\ -sin alpha, text n — text end\ &cos=begin cos alpha, text n — text\ -cos alpha, text n — text end\ &mathrm,(alpha+pi n)=mathrm,alpha\ &mathrm,(alpha+pi n)=mathrm,alpha\ &sin<left(alpha+dfrac2right)>=cosalpha\ &cos<left(alpha+dfrac2right)>=-sin alpha\ &,mathrm,left(alpha+dfrac2right)=-,mathrm,alpha\ &,mathrm,left(alpha+dfrac2right)=-,mathrm,alpha end]

Пример 12. Решить систему (begin cos x=dfrac12\ sin x+cos x>0end)

Решением уравнения являются (x_1=dfrac3+2pi n, x_2=-dfrac3+2pi n, ninmathbb) . Подставим в неравенство (sin x+cos x>0) по очереди оба корня:

(sin x_1+cos x_1=dfrac2+dfrac12>0) , следовательно, корень (x_1) нам подходит;
(sin x x_2+cos x_2=-dfrac2+dfrac12 , следовательно, корень (x_2) нам не подходит.

Таким образом, решением системы являются только (x=dfrac3+2pi n, ninmathbb) .

Алгебраический способ.

Пример 13. Найти корни уравнения (sin x=dfrac2) , принадлежащие отрезку ([0;pi]) .

Решением уравнения являются (x_1=dfrac4+2pi n, x_2=dfrac4 +2pi n, ninmathbb) . Для того, чтобы отобрать корни, решим два неравенства: (0leq x_1leqpi) и (0leq x_2leqpi) :

(0leq dfrac4+2pi nleqpi Leftrightarrow -dfrac18leq nleqdfrac38) . Таким образом, единственное целое значение (n) , удовлетворяющее этому неравенству, это (n=0) . При (n=0) (x_1=dfrac4) — входит в отрезок ([0;pi]) .

Аналогично решаем неравенство (0leq x_2leqpi) и получаем (n=0) и (x_2=dfrac4) .

Для следующего примера рассмотрим алгоритм решения линейных уравнений в целых числах:

Уравнение будет иметь решение в целых числах относительно (x) и (y) тогда и только тогда, когда (c) делится на (НОД(a,b)) .

Пример: Уравнение (2x+4y=3) не имеет решений в целых числах, потому что (3) не делится на (НОД(2,4)=2) . Действительно, слева стоит сумма двух четных чисел, то есть четное число, а справа — (3) , то есть нечетное число.

Пример: Решить уравнение (3x+5y=2) . Т.к. (НОД(3,5)=1) , то уравнение имеет решение в целых числах. Выразим (x) через (y) :

Число (dfrac3) должно быть целым. Рассмотрим остатки при делении на (3) числа (y) : (0) , (1) или (2) .
Если (y) при делении на (3) имеет остаток (0) , то оно записывается как (y=3p+0) . Тогда [dfrac3=dfrac3=dfrac23-2pne text]

Если (y) при делении на (3) имеет остаток (1) , то оно записывается как (y=3p+1) . Тогда [dfrac3=dfrac3=-2p=text]

Значит, этот случай нам подходит. Тогда (y=3p+1) , а (x=dfrac3-y=-5p-1) .

Ответ: ((-5p-1; 3p+1), pinmathbb) .

Перейдем к примеру:

Пример 14. Решить систему [begin sin dfrac x3=dfrac2\[3pt] cos dfrac x2=1 end]

Решим первое уравнение системы:

[left[ begin begin &dfrac x3=dfrac3+2pi n\[3pt] &dfrac x3=dfrac3 +2pi m end end right.quad n,minmathbb quad Leftrightarrow quad left[ begin begin &x=pi+6pi n\ &x=2pi +6pi m end end right.quad n,minmathbb]

Решим второе уравнение системы:

[dfrac x2=2pi k, kinmathbb quad Leftrightarrow quad x=4pi k, kinmathbb]

Необходимо найти корни, которые удовлетворяют и первому, и второму уравнению системы, то есть пересечь решения первого и второго уравнений.
Найдем целые (n) и (k) , при которых совпадают решения в сериях (pi+6pi n) и (4pi k) :

[pi + 6pi n=4pi k quad Rightarrow quad 4k-6n=1]

Т.к. (НОД(4,6)=2) и (1) не делится на (2) , то данное уравнение не имеет решений в целых числах.

Найдем целые (m) и (k) , при которых совпадают решения в сериях (2pi +6pi m) и (4pi k) :

[2pi +6pi m=4pi k quad Rightarrow quad 2k-3m=1]

Данное уравнение имеет решение в целых числах. Выразим (k=frac2=m+frac2) .

Возможные остатки при делении (m) на (2) — это (0) или (1) .
Если (m=2p+0) , то (frac2=frac2=p+frac12ne ) целому числу.
Если (m=2p+1) , то (frac2=frac2=p+1= ) целому числу.

Значит, (m=2p+1) , тогда (k=3p+2) , (pinmathbb) .

Подставим либо (m) , либо (k) в соответствующую ему серию и получим окончательный ответ: (x=4pi k=4pi (3p+2)=8pi+12pi p, pinmathbb) .