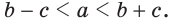Неравенства для медиан треугольника (8 видео)

Медиана треугольника

Определение . Медианой треугольника называют отрезок, соединяющий вершину треугольника с серединой противоположной стороны (рис 1).

Поскольку в каждом треугольнике имеется три вершины, то в каждом треугольнике можно провести три медианы.

На рисунке 1 медианой является отрезок BD .

Утверждение 1 . Медиана треугольника делит его на два треугольника равной площади ( равновеликих треугольника).

Доказательство . Проведем из вершины B треугольника ABC медиану BD и высоту BE (рис. 2),

и заметим, что (см. раздел нашего справочника «Площадь треугольника»)

Поскольку отрезок BD является медианой, то

что и требовалось доказать.

Утверждение 2 . Точка пересечения двух любых медиан треугольника делит каждую из этих медиан в отношении 2 : 1 , считая от вершины треугольника.

Доказательство . Рассмотрим две любых медианы треугольника, например, медианы AD и CE , и обозначим точку их пересечения буквой O (рис. 3).

Обозначим середины отрезков AO и CO буквами F и G соответственно (рис. 4).

Теперь рассмотрим четырёхугольник FEDG (рис. 5).

Сторона ED этого четырёхугольника является средней линией в треугольнике ABC . Следовательно,

Сторона FG четырёхугольника FEDG является средней линией в треугольнике AOC . Следовательно,

Отсюда вытекает, что точка O делит каждую из медиан AD и CE в отношении 2 : 1 , считая от вершины треугольника.

Следствие . Все три медианы треугольника пересекаются в одной точке.

Доказательство . Рассмотрим медиану AD треугольника ABC и точку O , которая делит эту медиану в отношении 2 : 1 , считая от вершины A (рис.7).

Поскольку точка, делящая отрезок в заданном отношении, является единственной, то и другие медианы треугольника будут проходить через эту точку, что и требовалось доказать.

Определение . Точку пересечения медиан треугольника называют центроидом треугольника.

Утверждение 3 . Медианы треугольника делят треугольник на 6 равновеликих треугольников (рис. 8).

Доказательство . Докажем, что площадь каждого из шести треугольников, на которые медианы разбивают треугольник ABC , равна площади треугольника ABC. Для этого рассмотрим, например, треугольник AOF и опустим из вершины A перпендикуляр AK на прямую BF (рис. 9).

Содержание

Неравенство треугольника — определение и вычисление с примерами решения
Неравенство треугольника
Свойства медианы треугольника. Итоговое повторение курса геометрии 7 – 9 класса
💡 Видео

Видео:Неравенства треугольника. 7 класс.Скачать

Неравенство треугольника — определение и вычисление с примерами решения

Содержание:

Неравенство треугольника:

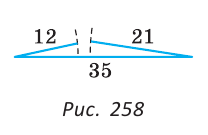
Опыт нам подсказывает, что путь из точки А в точку С по прямой АС короче, чем по ломаной ABC (рис. 255), т. е. АС 12+21 (рис. 258).

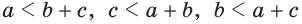
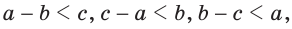
Замечание. Из неравенств треугольника следует, что то есть любая сторона треугольника больше разности двух других его сторон. Так, для стороны а справедливо

Пример:

Внутри треугольника ABC взята точка М (рис. 259). Доказать, что периметр треугольника АМС меньше периметра треугольника ABC.

Решение:

Так как у треугольников ABC и АМС сторона АС — общая, то достаточно доказать, что AM + МС B (рис. 108, а).

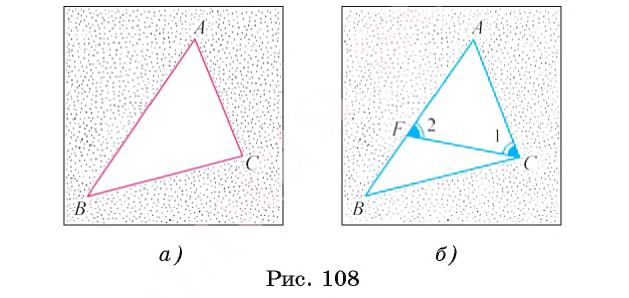
2) Отложим на стороне АВ отрезок АF, равный стороне AC (рис. 108, б).

3) Так как АF 1.

4) Угол 2 является внешним углом треугольника ВFС, следовательно, 2 > B.

5) Так как треугольник FАС является равнобедренным, то 1 = 2.

Таким образом, BСА > 1, 1 = 2 и 2 > B.

Отсюда получаем, что ВСА > B.

Теорема 2. В треугольнике против большего угла лежит большая сторона.

1) Пусть в треугольнике АBС С > B. Докажем, что АВ > АС (см. рис. 108, а). Доказательство проведем методом от противного.

2) Предположим, что это не так. Тогда: либо АВ = АС, либо АВ C.

В каждом из этих случаев получаем противоречие с условием: C > B. Таким образом, сделанное предположение неверно и, значит, АВ > АС.

Из данной теоремы следует утверждение: в прямоугольном треугольнике катет меньше гипотенузы.

Действительно, гипотенуза лежит против прямого угла, а катет — против острого. Поскольку прямой угол больше острого, то по теореме 2 получаем, что гипотенуза больше катета.

Теорема 3 (признак равнобедренного треугольника). Если два угла треугольника равны, то треугольник равнобедренный.

Пусть в треугольнике два угла равны. Тогда равны стороны, лежащие против этих углов. В самом деле, если предположить, что одна из указанных сторон больше другой, то по теореме 1 угол, лежащий против этой стороны, будет больше угла, лежащего против другой стороны, что противоречит условию равенства углов.

Значит, наше предположение неверно и в треугольнике две стороны равны, т. е. треугольник является равнобедренным.

Неравенство треугольника

Докажем, что длина каждой стороны треугольника меньше суммы длин двух других сторон.

Теорема 4. Длина каждой стороны треугольника меньше суммы длин двух других его сторон.

1) Пусть ABC — произвольный треугольник. Докажем, например, что выполняется неравенство АВ l, следовательно, верно неравенство АВF > 2.

4) Так как в треугольнике против большего угла лежит большая сторона (теорема 2), то АВ

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Видео:Построение медианы в треугольникеСкачать

Свойства медианы треугольника. Итоговое повторение курса геометрии 7 – 9 класса

Свойства медианы треугольника

Итоговое повторение курса геометрии 7 – 9 класса

При изучении какой-либо темы школьного курса можно отобрать определенный минимум задач, овладев методами решения которых, учащиеся будут в состоянии решить любую задачу на уровне программных требований по изучаемой теме. Предлагаю рассмотреть задачи, которые позволят увидеть взаимосвязи отдельных тем школьного курса математики. Поэтому составленная система задач является эффективным средством повторения, обобщения и систематизации учебного материала в ходе подготовки учащихся к экзамену.

Для сдачи экзамена не лишними будут дополнительные сведения о некоторых элементах треугольника. Рассмотрим свойства медианы треугольника и задачи, при решении которых этими свойствами можно воспользоваться. В предложенных задачах реализуется принцип уровневой дифференциации. Все задачи условно поделены на уровни (уровень указан в скобках после каждого задания).

Вспомним некоторые свойства медианы треугольника

Свойство 1. Докажите, что медиана треугольника ABC, проведённая из вершины A, меньше полусуммы сторон AB и AC.

Отложим на продолжении медианы AM за точку M отрезок MK, равный AM. Тогда в четырёхугольнике ABKC диагонали пересекаются и точкой пересечения делятся пополам. Значит, ABKC — параллелограмм. Применяя неравенство треугольника к треугольнику ABK, получим, что

то, сложив почленно эти три неравенства, получим, что

2AM + BN + CK > AB + BC + AC.

Отсюда следует, что AM + BN + CK > (AB + BC + AC).

Отложим на продолжении медианы AM за точку M отрезок MA1, равный AM. Тогда ABA1C — параллелограмм. Поэтому

BA1 = AC, 2AM = AA1 SDEF’ , то SAED+SBFD>SDEF , следовательно, указанным образом расположить точки невозможно.

так расположить точки нельзя.

Источник: Окружная олимпиада (Москва) , 2008 г, 11 класс

№32 Темы: Удвоение медианы. Ортоцентр и ортотреугольник Сложность:5 + Три точки, лежащие на одной прямой Подобные треугольники Классы: 9,10

В неравнобедренном треугольнике ABC точки H и M – точки пересечения высот и медиан соответственно. Через вершины A , B и C проведены прямые, перпендикулярные прямым AM , BM , CM соответственно. Докажите, что точка пересечения медиан треугольника, образованного проведенными прямыми, лежит на прямой MH .

Решение

Пусть A’B’C’ – треугольник, образованный

проведенными прямыми и G – точка пересечения его

медиан. Мы докажем, что M является серединой отрезка GH . Достроим треугольник BMC до параллелограмма BMCA1 . Отрезок MA1 делит сторону BC пополам, поэтому A1 лежит на прямой AM , причем AM = A1M (поскольку точка M делит медиану в отношении 2:1 ). Кроме того, BA1|| MC A’B’ и CA1|| MB A’C’ , поэтому BA1 и CA1 – высоты треугольника BA’C , значит A1 является ортоцентром треугольника BA’C , и

A’A1 BC . Стороны треугольника BA1M перпендикулярны

сторонам треугольника A’B’C’ соответственно, поэтому эти треугольники подобны, причем соответствующие прямые BC и

AG , содержащие медианы этих треугольников,

перпендикулярны. Значит, прямая A’G совпадает с прямой A’A1 . Пусть G’ – точка, симметричная точке H относительно M . Треугольники AHM и A1G’M симметричны относительно M , поэтому A1G’|| AH BC . Отсюда следует, что G’ лежит на прямой A’G . Аналогично, получаем, что G’ лежит на прямой B’G , то есть G’ совпадает с G .

Источник: Всероссийская олимпиада по математике, 2008 г, 9 класс

Отрабатываем умение: самостоятельно решать задачи.

Свойства медианы. Площадь треугольника

1. В треугольнике АВС медиана АМ перпендикулярна медиане BN. Найдите площадь треугольника АВС, если длина АМ равна 3, а длина BN равна 4.

2. Основание равнобедренного треугольника равно 2. Медианы, проведенные к боковым сторонам, взаимно перпендикулярны. Найдите площадь треугольника.

3. Две медианы равнобедренного треугольника взаимно перпендикулярны. Боковая сторона равна . Найдите площадь треугольника.

4. В треугольнике АВС медианы АD и ВE перпендикулярны, , . Чему равен квадрат третьей стороны?

5. Сторона треугольника равна 20, а медианы, проведенные к двум другим сторонам – 24 и 18. Найдите площадь треугольника.

6. Стороны треугольника равны 13, 14 и 15. Найти площади треугольников, на которые разбивается данный треугольник его медианами.

7. Площадь треугольника АВС равна 12. Из вершины тупого угла В проведена медиана BD, длина которой равна 3. Найдите длину стороны АС, если угол ABD – прямой.

8. Найдите площадь треугольника, если две его стороны равны 1 и , а медиана третьей стороны равна 2. (Указание – достроить до параллелограмма).

О т в е т: .

1. Одна сторона треугольника равна а, другая – b. Найдите третью сторону, если известно, что она равна медиане, проведенной к ней.

О т в е т: .

2. Основание равнобедренного треугольника , медиана боковой стороны 5. Найдите длины боковых сторон.

3. В равнобедренном треугольнике основание равно , а угол при основании равен 300. Найдите длину медианы, проведенной к боковой стороне.

4. Медианы треугольника равны 5, и . Докажите, что треугольник прямоугольный.

5. Числа , и выражают длины медиан некоторого треугольника. Докажите, что если выполняется равенство , то треугольник является прямоугольным.

Медиана, проведенная к гипотенузе

1. Медиана, проведенная к гипотенузе прямоугольного треугольника, равна 3 см и делит прямой угол в отношении 2:1. Найдите меньший катет.

2. АА1, ВВ1, СС1 – медианы треугольника АВС. . Найдите .

3. Медианы треугольника АВС АА1, ВВ1 и СС1 пересекаются в точке О. .см. см. Найдите ВО.

4. Гипотенуза прямоугольного треугольника в 4 раза больше проведенной к ней высоты. Найдите острые углы треугольника.

О т в е т: 150; 750.

5. В трапеции ABCD углы при основании AD равны 200 и 700, длина отрезка, соединяющего середины оснований, равна 3. Найдите длину отрезка, соединяющего середины диагоналей трапеции.

· , , Ленинградские математические кружки

· , Задачи по планиметрии, Издательство МЦНМО, 2001г

· интернет сайт http://zadachi. ***** Задачи по геометрии

· Всероссийская олимпиада по математике, 2008 год,

· Турнир им. Ломоносова, 2001 год

· Московская математическая регата, 2012/13 г, 8 класс