Назовите две пары параллельных граней прямой призмы abcda1b1c1d1 если ее основание трапеция (7 видео)

Вариант 1

Вариант 1.

А1. A1 D

Какие из следующих пар прямых являются B1 C1 скрещивающимися? A

Укажите плоскость, параллельную прямой, D C

проходящей через точки пересечения B

диагоналей граней AA1B1B и BB1C1C A

Основание призмы – правильный треугольник со A1 B1

стороной 6, а её боковое ребро равно 8 и

наклонено к плоскости основания под углом 600. C1

Найдите объём призмы.

A B

А4. B1 C1

Высота правильной четырёхугольной призмы

ABCDA1B1C1D1 равна 4, а сторона основания A1

– 4. Найдите расстояние между вершиной C и

точкой пересечения диагоналей боковой

грани AA1B1B C

1) 2 2) 4 3) 4 4) 2

Основание прямой призмы – прямоугольник со сторонами 4 и 3, а её высота равна 3. Найдите тангенс угла между диагональю призмы и плоскостью большей по площади боковой грани.

1) 2) 3) 4)

Высота правильной шестиугольной призмы равна 3, а площадь основания — . Найдите длину большей диагонали призмы.

Высота правильной четырёхугольной призмы ABCDA1B1C1D1 равна , а сторона основания — . На продолжении бокового ребра BB1 за точку B1 отложен отрезок B1K, равный ребру BB1. Найдите площадь сечения, проходящего через точки A,C и K.

Сторона основания правильной четырёхугольной призмы ABCDA1B1C1D1 равна 8, а боковое ребро – 6. Точка К – середина отрезка ВС, точка О – середина отрезка СD1. Найдите объём многогранника AA1KO.

В правильной четырёхугольной призме боковое ребро равно стороне основания. Найдите угол между диагональю призмы и скрещивающейся с ней диагональю боковой грани.

А1. A B

Какие из следующих пар прямых являются D C

Укажите плоскость, параллельную прямой, B C

проходящей через точки пересечения

диагоналей граней AA1D1D и AA1B1B A D

1) B1C1D1 2) BDA1 3) BDD1 4) B1CC1 B1 C1

A1 D1

Основание призмы – правильный треугольник с A1 B1

высотой, равной , а её боковое ребро равно и

наклонено к плоскости основания под углом 600. C1

Найдите объём призмы.

1) 2)

A B

А4. B1 C1

Высота правильной четырёхугольной призмы

ABCDA1B1C1D1 равна , а сторона основания A1

– 2. Найдите расстояние между вершиной C и

точкой пересечения диагоналей боковой

грани AA1B1B C

1) 2,5 4)

Основание прямой призмы – прямоугольник со сторонами 4 и 3, а её высота равна 3. Найдите тангенс угла между диагональю призмы и плоскостью меньшей по площади боковой грани.

1) 2) 3) 4)

Высота правильной шестиугольной призмы равна 2, а площадь основания — . Найдите меньшую диагональ призмы.

Высота правильной четырёхугольной призмы ABCDA1B1C1D1 равна , а сторона основания — 8. На продолжении ребра АА1 за точку А1 отложен отрезок А1М, равный высоте призмы. Найдите площадь сечения, проходящего через точки B,D и M.

Сторона основания правильной четырёхугольной призмы ABCDA1B1C1D1 равна 16, а боковое ребро – 12. Точка М – середина стороны основания АD, точка Р – середина отрезка АВ1. Найдите объём многогранника СС1РМ.

А1. A B

Какие из следующих пар прямых являются D C

1) A1D1 и B1C1 2) BC1 и AD13) AD1 и A1D 4) AB1 и A1D1

Укажите плоскость, параллельную прямой, B C

проходящей через точки пересечения

диагоналей граней AA1D1D и B1BCC1 A D

1) B1C1D 2) BDA1 3) AA1B 4) B1CC1 B1 C1

A1 D1

Основание призмы – правильный треугольник. А1 В1

Радиус окружности, описанной около основания равен , С1

а её боковое ребро равно и наклонено к плоскости

основания под углом 600.

Найдите объём призмы. А В

1) К

А4. B1 C1

Основание прямой четырёхугольной призмы

ABCDA1B1C1D1 — прямоугольник со сторонами А1

АВ=6 и ВС=12. Высота призмы равна 8.

Найдите расстояние между вершиной С и точкой

пересечения диагоналей грани AA1B1B .

1) 6,5 4)

Основание прямой четырёхугольной призмы – прямоугольник со сторонами 8 и 6, а её высота равна 6. Найдите синус угла между диагональю призмы и плоскостью большей по площади боковой грани.

1) 2) 3) 4)

Высота правильной шестиугольной призмы равна 3, а радиус окружности, вписанной в основание, . Найдите длину большей диагонали призмы.

Высота правильной четырёхугольной призмы ABCDA1B1C1D1 равна , а сторона основания — 6. На продолжении ребра BB1 за точку B1 отложен отрезок B1К, равный половине ребра BB1. Найдите площадь сечения, проходящего через точки А, С и К.

В основании прямоугольного параллелепипеда MNPQM1N1P1Q1 лежит квадрат со стороной 8, боковое ребро равно 6. Точка К – середина отрезка M1N1, точка О – середина отрезка N1P. Найдите объём многогранника QQ1КО.

А1. A B

Какие из следующих пар прямых являются D C

Укажите плоскость, параллельную прямой, B C

проходящей через точки пересечения

диагоналей граней ABCD и AA1B1B A D

1) B1C1D 2) B1CC1 3) BDD1 4) BDA1 B1

A1 D1

В основании наклонной призмы лежит правильный А1 В1

треугольник. Радиус окружности, вписанной в основание, С1

равен , а её боковое ребро, равное 4, наклонено к

плоскости род углом 600. Найдите объём призмы.

1) 54 2) 18

А В

А4. B1 C1

В основании прямой четырёхугольной призмы

ABCDA1B1C1D1 лежит прямоугольник со А1

сторонами АВ=6 и ВС=12. Высота призмы — 8.

Найдите расстояние между вершиной А и точкой

пересечения диагоналей грани B1BСС1. С

1) 4)

В основании прямой четырёхугольной призмы лежит прямоугольник со сторонами 4 и 3, а её высота равна 3. Найдите синус угла между диагональю призмы и плоскостью меньшей по площади боковой грани.

1) 2) 3) 4)

Высота правильной шестиугольной призмы равна 2, а радиус окружности, вписанной в основание, . Найдите меньшую диагональ призмы.

Высота правильной четырёхугольной призмы ABCDA1B1C1D1 равна , а сторона основания — 12. На продолжении ребра АА1 за точку А1 отложен отрезок А1М, равный половине высоте призмы. Найдите площадь сечения, проходящего через точки B,D и M.

Сторона основания правильной четырёхугольной призмы EFGHE1F1G1H1 – квадрат со стороной 16, а боковое ребро равно 12. Точка М – середина отрезка E1H1, точка Р – середина отрезка GH1. Найдите объём многогранника FF1РМ.

А1. A B

Какие из следующих пар прямых являются D C

Укажите плоскость, параллельную прямой, B C

проходящей через точки пересечения

диагоналей граней СС1D1D и AA1B1B A D

1) B1C1D 2) BDA1 3) BDD1 4) B1CС1 B1

A1 D1

Основание наклонной призмы – ромб с

меньшей диагональю 4 и углом 600, а её боковое D1 C1

ребро, равное , наклонено к плоскости

основания под углом 600. A B

Найдите объём призмы.

1) 2)K

А4. B1 C1

Высота правильной четырёхугольной призмы

ABCDA1B1C1D1 равна 8, а сторона основания A1

– 8. Найдите расстояние между вершиной A и

точкой пересечения диагоналей

грани DD1C1C. C

1) 4 2) 8 3) 8 4) 4

В основании прямой четырёхугольной призмы лежит прямоугольник со сторонами 12 и 9, а её высота равна 9. Найдите котангенс угла между диагональю призмы и плоскостью большей по площади боковой грани.

1) 2) 3) 4)

Большая диагональ правильной шестиугольной призмы равна 5, а площадь основания — . Найдите высоту призмы.

Высота правильной четырёхугольной призмы ABCDA1B1C1D1 равна , а сторона основания — . На продолжении бокового ребра BB1 за точку B1 отложен отрезок B1K так, что отношение BK : B1K=2:1. Найдите площадь сечения, проходящего через точки A,C и K.

Сторона основания правильной четырёхугольной призмы ABCDA1B1C1D1 равна 4, а боковое ребро – 3. Точка К – середина отрезка АD, точка О – середина отрезка СD1. Найдите объём многогранника ВВ1KO.

Какие из следующих пар прямых являются В

скрещивающимися? С1

1) А1В1 и СВ 2) DС и D1С1 D

Укажите плоскость, параллельную прямой, B C

проходящей через точки пересечения

диагоналей граней СС1D1D и A1B1С1D1 A D

1) B1C1D 2) B1CС1 3) BDD1 4) BDA1 B1 С1

A1 D1

Основание призмы – ромб с меньшей диагональю

4 и углом 1200, её боковое ребро наклонено к D1 C1

плоскости основания под углом 600 и равно

. Найдите объём призмы. А

1) 2)

А4. B1 C1

Высота правильной четырёхугольной призмы

ABCDA1B1C1D1 равна , а сторона основания A1

– 2. Найдите расстояние между вершиной A и

точкой пересечения диагоналей

грани DD1C1C. C

1) 2,5 4)

Основание прямой призмы — прямоугольник со сторонами 4 и 3, а её высота равна 3. Найдите котангенс угла между диагональю призмы и плоскостью большей по площади боковой грани.

1) 2) 3) 4)

Длина меньшей диагонали правильной шестиугольной призмы равна 4, а площадь основания — . Найдите высоту призмы.

Высота правильной четырёхугольной призмы ABCDA1B1C1D1 равна , а сторона основания — 8. На продолжении ребра АА1 за точку А1 отложен отрезок А1М так, что отношение высоты призмы к отрезку АМ равно 1:2. Найдите площадь сечения, проходящего через точки B,D и M.

Сторона основания правильной четырёхугольной призмы ABCDA1B1C1D1 равна 4, а боковое ребро – 3. Точка М – середина стороны основания СD,

точка Р – середина отрезка А1D . Найдите объём многогранника ВВ1РМ.

Какие из следующих пар прямых являются В

скрещивающимися? С1

1) MQ и P1N1 2) QP и MN D

Укажите плоскость, параллельную прямой, B C

проходящей через точки пересечения

диагоналей граней D1D СС1 и ABСD A D

1) B1CС1 2) BDA1 3) B1C1D 4) BDD1 B1 С1

A1 D1

Основание призмы – ромб с большей диагональю

и углом 1200, а её боковое ребро равно D1

и наклонено к плоскости основания C1

Найдите объём призмы.

1) 2) К

D C

А4. B1 C1

В основании прямой четырёхугольной призмы

ABCDA1B1C1D1 — прямоугольник с основаниями А1

АВ=12 и ВС=24. Высота призмы равна 16.

Найдите расстояние между вершиной А и точкой

пересечения диагоналей грани DD1С1С. С

1) 4)

В основании прямой четырёхугольной призмы лежит прямоугольник со сторонами 4 и 3, а её высота равна 3. Найдите косинус угла между диагональю призмы и плоскостью большей по площади боковой грани.

1) 2) 3) 4)

Площадь основания правильной шестиугольной призмы равна . Найдите длину большей диагонали призмы, если она составляет с плоскостью основания угол 450.

Высота правильной четырёхугольной призмы ABCDA1B1C1D1 равна , а сторона основания -6. На продолжении бокового ребра BB1 за точку B1 отложен отрезок B1Т так, что отношение B1Т : ВB1 равно 1 : 2. Найдите площадь сечения, проходящего через точки A,C и Т.

Боковое ребро прямого параллелепипеда MNPQM1N1P1Q1 равно 9, основание — квадрат со стороной 12. Точка К – середина отрезка M1N1, точка О – середина отрезка N1P. Найдите объём многогранника QQ1КО.

Видео:№114. Изобразите параллелепипед ABCDA1B1C1D1 и отметьте на ребре АВ точку М. Постройте сечение паралСкачать

Геометрия. 10 класс

Призма

Заполните пропуски в тексте.

Используя рисунок, посчитайте у данного многогранника количество вершин , ребер , граней . Количество боковых ребер равно , а количество боковых граней – .

Призма

Найдите для каждой картинки пару (многогранник-сечение)

Призма

Какие из перечисленных объектов могут быть элементами призмы? Выделите их цветом.

Призма

Дополните схему подписями

Призма

многогранник, составленный из двух многоугольников, расположенных в двух равных плоскостях и n – параллелограммов

многогранник, составленный из двух равных многоугольников, и n – параллелограммов

многогранник, составленный из двух равных многоугольников, расположенных в двух плоскостях и n – параллелограммов

многогранник, составленный из двух равных многоугольников, расположенных в параллельных плоскостях и n – параллелограммов

Призма

Основанием прямой треугольной призмы является прямоугольный треугольник с катетами 15 см и 20 см. Площадь большей боковой грани равна 75 см 2 . Вычисли высоту призмы.

Нам дана площадь большей боковой грани. Какая из граней будет большей? Поскольку призма , то ее грани – . Боковые ребра призмы между собой. Значит больше будет та грань, сторона которой является большей в основании. В основании лежит прямоугольный треугольник, значит большей стороной будет .

С помощью можем вычислить длину гипотенузы. Она равна 25 см.

Площадь равна 75 см 2 , то есть площадь прямоугольника равна 75 см 2 . Зная, что одна сторона этого прямоугольника равна 25см, сможем найти длину второй стороны. Получим 3 (75:25=3). Высота прямой призмы равна , значит высота равна

Видео:Прямая, параллельная основаниям трапеции ABCD, пересекает её боковые #математика #огэ #впрСкачать

Назовите две пары параллельных граней прямой призмы abcda1b1c1d1 если ее основание трапеция

БАЗА ЗАДАНИЙ

Задание № 5. Стереометрия.

1. Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсеченной треугольной призмы равна 8. Найдите площадь боковой поверхности исходной призмы.

2. Через среднюю линию основания треугольной призмы, объем которой равен 32, проведена плоскость, параллельная боковому ребру. Найдите объем отсеченной треугольной призмы.

3. Во сколько раз увеличится площадь поверхности куба, если его ребро увеличить в три раза?

4. Площадь поверхности куба равна 24. Найдите его объем.

5. Если каждое ребро куба увеличить на 1, то его площадь поверхности увеличится на 30. Найдите ребро куба.

6. Площадь поверхности куба равна 8. Найдите его диагональ.

7. Объем куба равен 24√3. Найдите его диагональ.

8. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 3 и 5. Объем призмы равен 30. Найдите ее боковое ребро.

9. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 3 и 4. Площадь ее поверхности равна 132. Найдите высоту призмы.

10. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, боковое ребро равно 5. Найдите объем призмы.

11. Найдите боковое ребро правильной четырехугольной призмы, если сторона ее основания равна 20, а площадь поверхности равна 1760.

12. Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 6 и 8, и боковым ребром, равным 10.

13. В основании прямой призмы лежит ромб с диагоналями, равными 9 и 12. Площадь ее поверхности равна 468. Найдите боковое ребро этой призмы.

14. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2. Объем параллелепипеда равен 6. Найдите площадь его поверхности.

15. Три ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 4, 6, 9. Найдите ребро равновеликого ему куба.

16. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 3. Объем параллелепипеда равен 36. Найдите его диагональ.

17. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 4. Диагональ параллелепипеда равна 6. Найдите объем параллелепипеда.

18. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2. Площадь поверхности параллелепипеда равна 16. Найдите его диагональ.

19. Диагональ прямоугольного параллелепипеда равна √8 и образует углы 30°,30° и 45° с плоскостями граней параллелепипеда. Найдите объем параллелепипеда.

20. В прямоугольном параллелепипеде ABCDA 1 B 1 C 1 D 1 известно, что BB 1 =32, AB=12, AD=9. Найдите площадь сечения проходящее через вершины A, A 1 , C.

22. Дана правильная четырёхугольная призма ABCDA 1 B 1 C 1 D 1 , площадь основания которой равна 6, а боковое ребро равно 7. Найдите объём многогранника, вершинами которого являются точки A, B, C, B 1 .

23. Найдите объём многогранника, вершинами которого являются точки C, A₁ , B₁ , C₁ правильной треугольной призмы ABCA₁B₁C₁ , площадь основания которой равна 4, а боковое ребро равно 9.

24. Найдите объём многогранника, вершинами которого являются точки A, C, A 1 , B₁, C 1 правильной треугольной призмы ABCA 1 B 1 C 1 . Площадь основания призмы равна 7, а боковое ребро равно 9.

25. В правильной треугольной призме ABCA ₁ B ₁ C ₁ все ребра равны 3. Найдите угол между прямыми AA₁и BC₁. Ответ дайте в градусах.

26. В правильной треугольной призме ABCA ₁ B ₁ C ₁ известно, что AB=√3AA ₁ . Найдите угол между прямыми AB₁ и CC₁. Ответ дайте в градусах.

27. Объём куба равен 16. Найдите объём треугольной призмы, отсекаемой от куба плоскостью, проходящей через середины двух рёбер, выходящих из одной вершины, и параллельной третьему ребру, выходящему из этой же вершины.

28. Объем куба равен 12. Найдите объем четырехугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба.

29. Объем параллелепипеда ABCDA 1 B 1 C 1 D 1 равен 4,5. Найдите объем треугольной пирамиды AD 1 CB 1 .

30. Объем параллелепипеда ABCDA 1 B 1 C 1 D 1 равен 1,5. Найдите объем треугольной пирамиды ABCB 1 .

31. Найдите объем параллелепипеда ABCDA 1 B 1 C 1 D 1 , если объем треугольной пирамиды ABDA 1 равен 3.

32. Гранью параллелепипеда является ромб со стороной 1 и острым углом 60°. Одно из ребер параллелепипеда составляет с этой гранью угол 60° и равно 2. Найдите объем параллелепипеда.

33. Найдите объём многогранника ACDFA 1 C 1 D 1 F 1 правильной шестиугольной призмы ABCDEFA 1 B 1 C 1 D 1 E 1 F 1 , площадь основания которой равна 9, а боковое ребро равно 11.

34. В правильной шестиугольной призме ABCDEFA 1 B 1 C 1 D 1 E 1 F 1 , стороны основания которой равны 5, а боковые рёбра равны 11, найдите расстояние от точки A до прямой E 1 D 1 .

35. Найдите объём многогранника DA 1 B 1 C 1 D 1 E 1 F 1 правильной шестиугольной призмы ABCDEFA 1 B 1 C 1 D 1 E 1 F 1 , площадь основания которой равна 12, а боковое ребро равно 2.

36. Найдите объём многогранника CDEC 1 D 1 E 1 правильной шестиугольной призмы ABCDEFA 1 B 1 C 1 D 1 E 1 F 1 , площадь основания которой равна 6, а боковое ребро равно 14.

37. Найдите объём многогранника A 1 B 1 F 1 A правильной шестиугольной призмы ABCDEFA 1 B 1 C 1 D 1 E 1 F 1 , площадь основания которой равна 12, а боковое ребро равно 15.

38. В правильной четырёхугольной пирамиде высота равна 2, боковое ребро равно 5. Найдите её объём.

39. В правильной четырёхугольной пирамиде боковое ребро равно 7,5, а сторона основания равна 10. Найдите высоту пирамиды.

40. Найдите площадь поверхности правильной четырехугольной пирамиды, стороны основания которой равны 6 и высота равна 4.

41. В правильной четырехугольной пирамиде высота равна 12, объем равен 200. Найдите боковое ребро этой пирамиды.

42. В правильной треугольной пирамиде боковое ребро равно 7, а сторона основания равна 10,5. Найдите высоту пирамиды.

📺 Видео

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Стереометрия 10 класс. Часть 2 | Математика | TutorOnlineСкачать

№233. Основанием прямой призмы АВСA1B1C1 является прямоугольный треугольник ABCСкачать

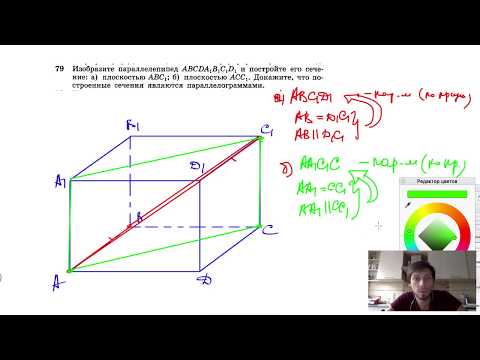
№79. Изобразите параллелепипед ABCDA1B1C1D1 и постройте его сечение: а) плоскостью АВС1;Скачать

СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать

№344. Диагонали куба ABCDA1B1C1D1 пересекаются в точке О. Найдите число k такое,Скачать

№81. Изобразите параллелепипед ABCDA1B1C1D1 и отметьте точки М и N соответственноСкачать

Урок 8. Угол между плоскостями. Стереометрия с нуля.Скачать

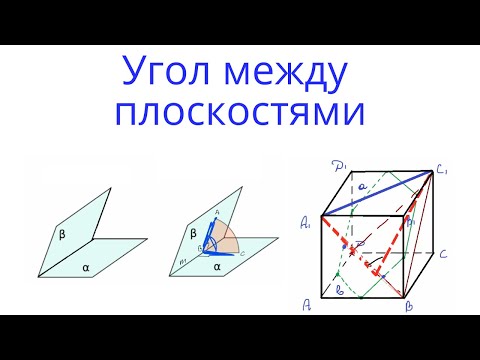
№109. Две плоскости, каждая из которых содержит два боковых ребра параллелепипеда, не принадлежащихСкачать

Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

ЕГЭ №14. Задачи по стереометрии. 10-11 класс | Математика TutorOnlineСкачать

35. Геометрия на ЕГЭ по математике. Трапеция.Скачать

Профильный ЕГЭ 2023. Задача 13. Построение сечений. Стереометрия. 10 классСкачать

Геометрия Прямая, параллельная основаниям трапеции ABCD, пересекает её боковые стороны AB и CDСкачать

8 задание ЕГЭ по математике профильному.Объем параллелепипеда ABCDA1B1C1D1 равен 4,5. Найдите объемСкачать

10 класс, 30 урок, ПризмаСкачать

Вся стереометрия первой части в ЕГЭ | Математика ЕГЭ для 10 класса | УмскулСкачать

ЕГЭ-2021: Объём отсечённой призмы | Задание 8: СтереометрияСкачать