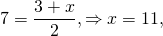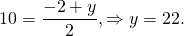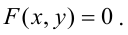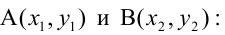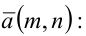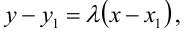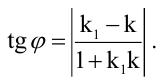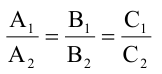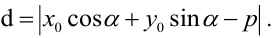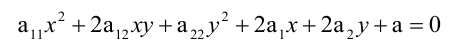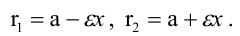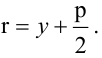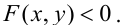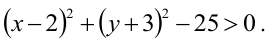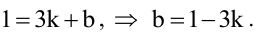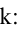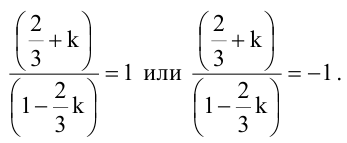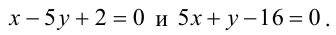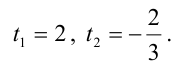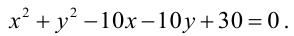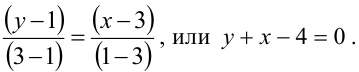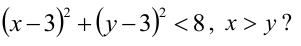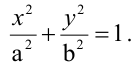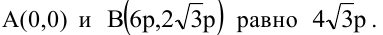Как найти уравнение окружности, симметричной данной?
Симметричные окружности имеют равные радиусы. Следовательно, остаётся найти координаты центра симметричной окружности (как точки, симметричной данной).
1) Окружность задана уравнением (x-3)²+(y+2)²=16. Составить уравнение окружности, симметричной данной относительно точки (7; 10).
Центр окружности (x-3)²+(y+2)²=16 — точка с координатами (3;-2). Найдём точку, симметричную ей относительно точки (7; 10).
Таким образом, центр окружности, симметричной данной, — точка с координатами (11;22). Подставляем в формулу уравнения окружности a=11, b=22, R²=16:
2) Окружность задана уравнением (x+5)²+(y+1)²=9. Составить уравнение окружности, симметричной данной относительно начала координат.
Центром данной окружности является точка (-5;-1). Точка, симметричная данной относительно начала координат — (5;1). Таким образом, для окружности, симметричной данной относительно точки O(0;0) a=5, b=1, R²=9:
3) Окружность задана уравнением (x-7)²+(y-2)²=12. Составить уравнение окружности, симметричной данной относительно прямой y=x.
Центр окружности (x-7)²+(y-2)²=12 — точка (7;2) — при симметрии относительно прямой y=x переходит в точку (2;7). Следовательно, a=2, b=7, R²=12 и искомое уравнение окружности:
4) Окружность задана уравнением (x+4)²+(y-5)²=19. Составить уравнение окружности, симметричной данной относительно прямой y=2x+4.
Центр окружности (x+4)²+(y-5)²=19 — точка (-4;5). Точку, симметричную точке (-4;5) относительно прямой y=2x+4, нашли в прошлый раз — (3,2; 1,4). Таким образом, a=3,2, b=1,4, R²=19 и уравнение симметричной окружности
5) Окружность задана уравнением (x+8)²+(y+3)²=4. Составить уравнение окружности, симметричной данной относительно прямой y= -1.
Центр окружности (x+8)²+(y+3)²=4 — (-8; -3). Точка, симметричная точке (-8; -3) относительно прямой y= -1, имеет такую же абсциссу, x= -8. Расстояние от точки (-8; -3) до прямой y= -1 равно -1-(-3)=2. Расстояние от прямой y= -1 до центра симметричной окружности также равно 2, отсюда -1+2=1 — это ордината центра. Таким образом, точка (-8; 1) — центр окружности, симметричной данной, а R²=4.
Следовательно, искомое уравнение окружности
Видео:Уравнение окружности (1)Скачать

Уравнение с двумя переменными и его график. Уравнение окружности
п.1. Понятие уравнения с двумя переменными
Мы уже знакомы со многими функциями и умеем их записывать в виде формул:
y = 2x + 5 – прямая, y = 5x 2 + 2x – 1 – парабола, (mathrm) – гипербола.
Если записать такое выражение: x 2 (x + y) = 1 – y – в нём тоже есть две переменные x и y, и постоянная 1.
Для наших примеров:
F(x; y) = 2x – y + 5 = 0 – прямая
F(x; y) = 5x 2 + 2x – y – 1 = 0 – парабола
F(x; y) = (mathrm) – y = 0 – гипербола
F(x; y)=x 2 (x + y) + y – 1 = 0 – некоторая кривая (график — ниже).
п.2. Обобщенные правила преобразования графика уравнения
Пусть F(x; y) = 0 – исходный график некоторой функции
Симметричное отображение относительно оси OY
Симметричное отображение относительно оси OX
Центральная симметрия относительно начала координат
Параллельный перенос графика на a единиц вправо
Параллельный перенос графика на a единиц влево
Параллельный перенос графика на b единиц вниз
Параллельный перенос графика на b единиц вверх
Сжатие графика к оси OY в a раз
Сжатие графика к оси OX в b раз
F(x; by) = 0
0 Например:
Окружность с центром в точке O(2; 1) и радиусом R = 3 задаётся уравнением: $$ mathrm $$
п.4. Примеры
Пример 1. Постройте график уравнения:
а) 2x + 7y – 14 = 0
Выразим y из уравнения: ( mathrm<y=frac=-frac + 2 > ) – это прямая
б) xy + 4 = 0
Выразим y из уравнения: ( mathrm<y=frac> ) – это гипербола
в) ( x+ 2) 2 + y 2 = 4
Это – уравнение окружности с центром O(–2; 0), радиусом ( mathrm<R=sqrt=2> )
г) x 2 + 5y – 2 = 0
Выразим y из уравнения: ( mathrm<y=frac> ) – это парабола
Пример 2*. Постройте график уравнения:
а) 2|x| + 5y = 10
( mathrm<y=frac=-frac25|x|+2> )
Строим график для ( mathrm ), а затем отражаем его относительно оси OY в левую полуплоскость.
б) 3x + |y| = 6
|y| = –3x + 6
Строим график для y > 0: y = –3x + 6, а затем отражаем его относительно оси OX в нижнюю полуплоскость.
в) |x| + |y| = 2
|y| = –|x| + 2
Строим график для x > 0, y > 0: y = –x + 2, а затем отражаем его относительно осей OX и OY.
г) |x – 1| + |y – 2| = 4
Получим тот же ромб (квадрат), что и в (в), но его центр будет перенесен из начала координат в точку O(1; 2).
д) (mathrm<frac+2|y-2|=4>)
Ромб по x растянется в 2 раза по диагонали, а по y – сожмётся в 2 раза по диагонали.
Пример 3. Постройте график уравнения:
а) x 2 + y 2 + 4x – 6y + 4 = 0
Выделим полные квадраты:
(x 2 + 4x + 4) + (y 2 – 6y + 9) – 9 = 0
(x + 2) 2 + (y – 3) 2 = 3 2 – уравнение окружности с центром (–2; 3), радиусом 3.
Видео:ГЕОМЕТРИЯ 9 класс: Уравнение окружности и прямойСкачать

Уравнения прямых и кривых на плоскости с примерами решения
Содержание:
Видео:9 класс, 6 урок, Уравнение окружностиСкачать

Уравнения прямых и кривых на плоскости
Уравнения кривых в большом количестве встречаются при чтении экономической литературы. Укажем некоторые из этих кривых.
Кривая безразличия — кривая, показывающая различные комбинации двух продуктов, имеющих одинаковое потребительское значение, или полезность, для потребителя.
Кривая потребительского бюджета — кривая, показывающая различные комбинации количеств двух товаров, которые потребитель может купить при данном уровне его денежного дохода.
Кривая производственных возможностей — кривая, показывающая различные комбинации двух товаров или услуг, которые могут быть произведены в условиях полной занятости и полного объема производства в экономике с постоянными запасами ресурсов и неизменной технологией.
Кривая инвестиционного спроса — кривая, показывающая динамику процентной ставки и объем инвестиций при разных процентных ставках.
Кривая Филлипса — кривая, показывающая существование устойчивой связи между уровнем безработицы и уровнем инфляции.
Кривая Лаффера — кривая, показывающая связь между ставками налогов и налоговыми поступлениями, выявляющая такую налоговую ставку, при которой налоговые поступления достигают максимума.
Уже простое перечисление терминов показывает, как важно для экономистов умение строить графики и анализировать уравнения кривых, каковыми являются прямые линии и кривые второго порядка — окружность, эллипс, гипербола, парабола. Кроме того, при решении большого класса задач требуется выделить на плоскости область, ограниченную какими-либо кривыми, уравнения которых заданы. Чаще всего эти задачи формулируются так: найти наилучший план производства при заданных ресурсах. Задание ресурсов имеет обычно вид неравенств, уравнения которых даны. Поэтому приходится искать наибольшее или наименьшее значения, принимаемые некоторой функцией в области, заданной уравнениями системы неравенств.
В аналитической геометрии линия на плоскости определяется как множество точек, координаты которых удовлетворяют уравнению
Пусть на плоскости задана прямоугольная декартова система координат. Прямая на плоскости может быть задана одним из уравнений:
1. Общее уравнение прямой:
Вектор 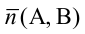
2. Уравнение прямой с угловым коэффициентом:
где 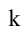
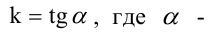
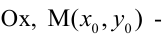
Уравнение (2.2) принимает вид 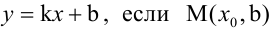
3. Уравнение прямой в отрезках:
где а и b — величины отрезков, отсекаемых прямой на осях координат.
4. Уравнение прямой, проходящей через две данные точки —
5. Уравнение прямой, проходящей через данную точку 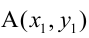
6. Нормальное уравнение прямой:
где 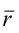
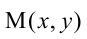
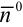
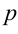
Нормальное уравнение прямой в координатной форме имеет вид:
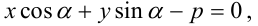
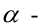
Уравнение пучка прямых с центром в точке 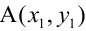
где 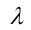
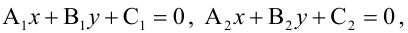
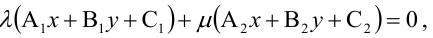
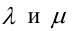
Величина угла между прямыми 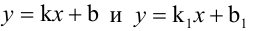
Равенство 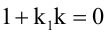
Для того, чтобы два уравнения

Уравнения (2.7), (2.8) задают две различные параллельные прямые, если 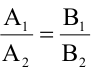
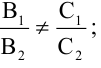
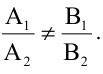
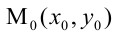
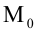
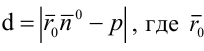
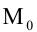
Общее уравнение кривой второго порядка имеет вид:
Предполагается, что среди коэффициентов уравнения 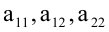
Уравнение окружности с центром в точке 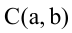

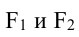
Эллипс, заданный уравнением (2.10), симметричен относительно осей координат.
Параметры а и b называются полуосями эллипса.
Пусть 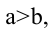
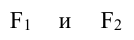
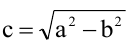
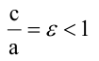
Расстояния от точки 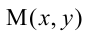
Если же 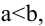
Если а=b, то эллипс является окружностью с центром в начале координат радиуса а.
Гиперболой называется геометрическое место точек, разность расстояний которых от двух данных точек 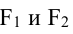
Каноническое уравнение гиперболы:
Гипербола, заданная уравнением (2.11), симметрична относительно осей координат. Она пересекает ось 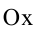
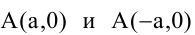
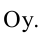
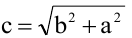
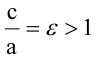
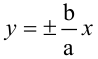
Расстояния от точки 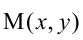
Гипербола, у которой а=b, называется равносторонней, ее уравнение 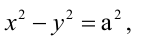
Гиперболы 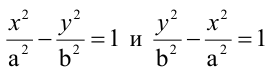
Каноническое уравнение параболы имеет два вида:
1. 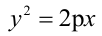
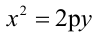
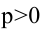
Парабола, уравнение которой 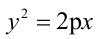
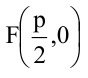
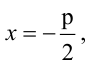
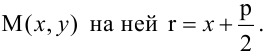
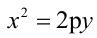
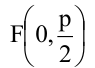
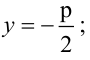
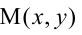
Уравнение 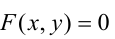
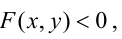
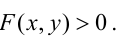
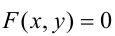
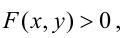
Прямая, уравнение которой 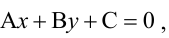
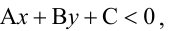
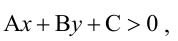
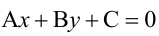
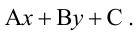
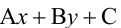
Точно так же решаются и нелинейные неравенства с двумя неизвестными.
Например, решим неравенство 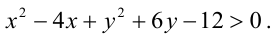
Уравнение 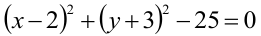
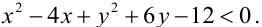
Пример:
Составьте уравнения прямых, проходящих через точку А(3,1) и наклоненных к прямой 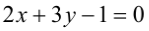
Решение:
Будем искать уравнение прямой в виде 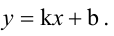
Величина угла между прямыми 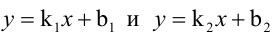
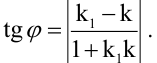
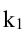
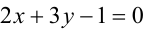
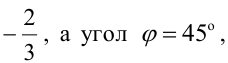
Имеем два значения 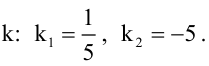
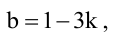
Пример:
При каком значении параметра t прямые, уравнения которых 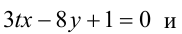
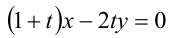
Решение:
Прямые, заданные общими уравнениями, параллельны, если коэффициенты при x и y пропорциональны, т.е. 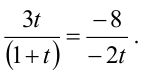
Пример:
Найти уравнение общей хорды двух окружностей: 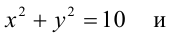
Решение:
Найдем точки пересечения окружностей, для этого решим систему уравнений: 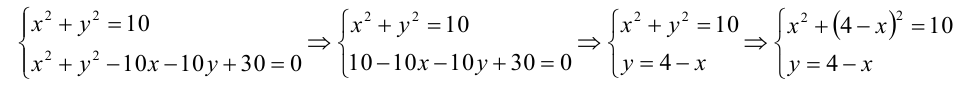
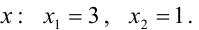
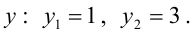
Пример:
Как расположены на плоскости точки, координаты которых удовлетворяют условиям
Решение:
Первое неравенство системы определяет внутренность круга, не включая границу, т.е. окружность с центром в точке (3,3) и радиуса 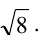
Пример:
Вычислить длину стороны квадрата, вписанного в эллипс, уравнение которого
Решение:
Пусть 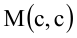
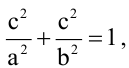
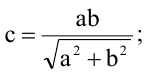
Пример:
Зная уравнение асимптот гиперболы 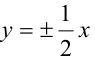
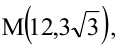
Решение:
Запишем каноническое уравнение гиперболы: 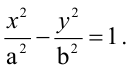
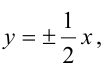
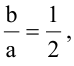
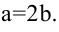
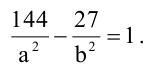
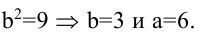
Пример:
Вычислить длину стороны правильного треугольника АВС, вписанного в параболу с параметром р, предполагая, что точка А совпадает с вершиной параболы.
Решение:
Каноническое уравнение параболы с параметром р имеет вид 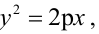
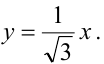
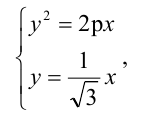
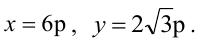
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Плоскость и прямая в пространстве
- Определитель матрицы
- Критерий совместности Кронекера-Капелли
- Формулы Крамера
- Производные тригонометрических функции
- Производная сложной функции
- Пределы в математике
- Функции многих переменных
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
💥 Видео
Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

начертить окружность. Привести уравнение окружности к стандартному виду. Координаты центра и радиус.Скачать

УРАВНЕНИЕ ОКРУЖНОСТИСкачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

9 класс, 7 урок, Уравнение прямойСкачать

Уравнение окружности. Практика. Урок 7. Геометрия 9 классСкачать

Длина окружности. Площадь круга. 6 класс.Скачать

Уравнение окружности | Геометрия 7-9 класс #90| ИнфоурокСкачать

10 класс, 11 урок, Числовая окружностьСкачать

Уравнение окружностиСкачать

🔴 ТРИГОНОМЕТРИЯ С НУЛЯ (Тригонометрическая Окружность на ЕГЭ 2024 по математике)Скачать

УРАВНЕНИЯ ОКРУЖНОСТИ И ПРЯМОЙ 9 класс геометрияСкачать

Тригонометрическая окружность. Как выучить?Скачать

№968. Напишите уравнение окружности с центром в точке А(0; 6), проходящей через точку В (-3; 2).Скачать

Отбор корней по окружностиСкачать

Найти центр и радиус окружностиСкачать