Дан Массив неотрицательных целых чисел. Найдите три элемента из этого массива, которые образуют треугольник с максимальным периметром.
Примеры :
Наивное решение:
Решение по грубой силе: проверить для всех комбинаций из 3 элементов, образует ли он треугольник или нет, и обновить максимальный периметр, если он образует треугольник. Сложность наивного решения составляет O (n 3 ). Ниже приведен код для этого.
// Решение грубой силы, чтобы найти
// вне максимального периметра треугольника, который
// может быть сформирован с использованием элементов
// данного массива
#include
#include
using namespace std;
// Функция для определения максимального периметра
void maxPerimeter( int arr[], int n)<
// инициализируем максимальный периметр
// подбираем 3 разных элемента
for ( int i = 0; i
for ( int j = i + 1; j
for ( int k = j + 1; k
// a, b, c — 3 стороны треугольника
// проверяем, формируются ли a, b, c
// треугольник или нет.
// если он образует треугольник
// затем обновляем максимальное значение.
maxi = max(maxi, a+b+c);
// Если максимальный периметр ненулевой
// затем распечатать его.
if (maxi) cout «Maximum Perimeter is: «
// иначе треугольник не образуется
else cout «Triangle formation «
«is not possible.»
// Программа для водителя
// тестовый пример 1
// контрольный пример 2
// тестовый пример 3
// Решение грубой силы, чтобы узнать максимум
// треугольник периметра, который может быть сформирован
// используя элементы данного массива
// Функция для определения максимального периметра
static void maxPerimeter( int arr[], int n)
// инициализируем максимальный периметр как 0.
// подбираем 3 разных элемента
for ( int i = 0 ; i 2 ; i++)
for ( int j = i + 1 ; j 1 ; j++)
for ( int k = j + 1 ; k
// a, b, c — 3 стороны
// проверяем, a, b, c
// образует треугольник или нет.
// если он образует треугольник
// затем обновляем максимум
maxi = Math.max(maxi, a+b+c);
// Если максимальный периметр ненулевой
// затем распечатать его.
System.out.println( «Maximum Perimeter is: «
// иначе треугольник не образуется
System.out.println( «Triangle formation «
+ «is not possible.» );
// Программа для водителя
public static void main (String[] args)
// тестовый пример 1
// контрольный пример 2
// тестовый пример 3
12 , 5 , 55 , 4 , 9 >;
// Этот код предоставлен anuj_67.
# Решение грубой силы, чтобы найти
№ из максимального периметра треугольника
# который может быть сформирован с использованием
# элементы данного массива
# Функция, чтобы узнать
# максимальный периметр
# подобрать 3 разных
# элементы из массива.
for i in range (n — 2 ):
for j in range (i + 1 , n — 1 ):
for k in range (j + 1 , n):
# a, b, c — 3 стороны
if (a + c and b + c
maxi = max (maxi, a + b + c)
return «Triangle formation is not possible»
return «Maximum Perimeter is: » + str (maxi)
arr1 = [ 6 , 1 , 6 , 5 , 8 , 4 ]
arr2 = [ 2 , 20 , 7 , 55 ,
arr3 = [ 33 , 6 , 20 , 1 , 8 ,
12 , 5 , 55 , 4 , 9 ]
if __name__ = = ‘__main__’ :
# Этот код добавлен
# Прита Updhayay
// Решение грубой силы, чтобы узнать
// максимальный периметр треугольника, который
// может быть сформирован с использованием элементов
// данного массива
// Функция, чтобы узнать
static void maxPerimeter( int []arr,
// подбираем 3 разных элемента
for ( int i = 0; i
for ( int j = i + 1; j
for ( int k = j + 1; k
// a, b, c — 3 стороны
// проверяем, a, b, c
// образует треугольник или нет.
// если он образует треугольник
// затем обновляем максимум
maxi = Math.Max(maxi, a + b + c);
// Если максимальный периметр
// не ноль, затем распечатать его.
Console.WriteLine( «Maximum Perimeter is: » + maxi);
// иначе треугольника нет
Console.WriteLine( «Triangle formation » +
«is not possible.» );
public static void Main ()
// тестовый пример 1
// контрольный пример 2
// тестовый пример 3
// Этот код предоставлен anuj_67.
// Решение грубой силы, чтобы найти
// вне максимального периметра треугольника, который
// может быть сформирован с использованием элементов
// данного массива
// Функция, чтобы узнать
// максимальный периметр
function maxPerimeter( $arr , $n )
// подбираем 3 разных
// элементы из массива.
for ( $i = 0; $i $n — 2; $i ++)
for ( $j = $i + 1; $j $n — 1; $j ++)
for ( $k = $j + 1; $k $n ; $k ++)
// a, b, c — 3 стороны
// проверяем, a, b, c
// образует треугольник или нет.
// если он образует треугольник
// затем обновляем максимальное значение.
$maxi = max( $maxi , $a + $b + $c );
// Если максимальный периметр
// не ноль, затем распечатать его.
echo «Maximum Perimeter is: » ;
// иначе треугольника нет
echo «Triangle formation » ;
echo «is not possible. n» ;
// тестовый пример 1
$arr1 = array (6, 1, 6, 5, 8, 4);
maxPerimeter( $arr1 , 6);
// контрольный пример 2
$arr2 = array (2, 20, 7, 55,
maxPerimeter( $arr2 , 8);
// тестовый пример 3
$arr3 = array (33, 6, 20, 1, 8,
maxPerimeter( $arr3 , 10);
// Этот код предоставлен anuj_67.
?>
Выход :
Эффективный подход:
Сначала мы можем отсортировать массив по возрастанию. Итак, первый элемент будет максимальным, а последний будет минимальным. Теперь, если первые 3 элемента этого отсортированного массива образуют треугольник, это будет треугольник с максимальным периметром, так как для всех других комбинаций сумма элементов (то есть периметр этого треугольника) будет = b> = c). a, b, c не могут образовывать треугольник, поэтому a> = b + c. As, b и c = c + d (если мы отбросим b и возьмем d) или a> = b + d (если мы отбросим c и возьмем d). Итак, мы должны бросить и забрать д.
Опять же набор анализа для b, c и d. Мы можем продолжать это до последнего и всякий раз, когда мы находим треугольник, образующий тройку, мы можем прекратить проверку, так как эта тройка дает максимальный периметр.
Следовательно, если в отсортированном массиве arr [i] Ниже приведена простая реализация этой концепции:
// Эффективное решение для поиска
// вне максимального периметра треугольника, который
// может быть сформирован с использованием элементов
// данного массива
#include
#include
using namespace std;
// Функция для определения максимального периметра
void maxPerimeter( int arr[], int n)<
// сортируем элементы массива
// в обратном порядке
sort(arr, arr+n, greater int >());
// цикл через отсортированный массив
// и проверяем, образует ли он
// треугольник или нет.
for ( int i = 0; i
// Проверяем, есть ли arr [i], arr [i + 1]
// и arr [i + 2] образует треугольник
// если он образует треугольник
// это треугольник с
maxi = max(maxi, arr[i] + arr[i+1] + arr[i+2]);
// Если максимальный периметр ненулевой
// затем распечатать его.
cout «Maximum Perimeter is: «
// иначе треугольник не образуется
cout «Triangle formation»
«is not possible.»
// Программа для водителя
// тестовый пример 1
// контрольный пример 2
// тестовый пример 3
// Эффективное решение для поиска
// вне максимального периметра треугольника, который
// может быть сформирован с использованием элементов
// данного массива
// Функция для определения максимального периметра
static void maxPerimeter( int arr[], int n) <
// сортируем элементы массива
// в обратном порядке
// сортировать (arr, arr + n, больше ());
// цикл через отсортированный массив
// и проверяем, образует ли он
// треугольник или нет.
for ( int i = 0 ; i 2 ; i++) <
// Проверяем, есть ли arr [i], arr [i + 1]
// и arr [i + 2] образует треугольник
if (arr[i] 1 ] + arr[i + 2 ]) <
// если он образует треугольник
// это треугольник с
maxi = Math.max(maxi, arr[i] + arr[i + 1 ] + arr[i + 2 ]);
// Если максимальный периметр ненулевой
// затем распечатать его.
System.out.println( «Maximum Perimeter is: » + maxi);
> // иначе треугольник не образуется
System.out.println( «Triangle formation is not possible.» );
// Функция возвращает отсортированный массив по убыванию
static int [] arrRevSort( int [] arr) <
Arrays.sort(arr, 0 , arr.length);
int j = arr.length — 1 ;
for ( int i = 0 ; i 2 ; i++, j—) <
// Программа для водителя
public static void main(String[] args) <
// тестовый пример 1
// контрольный пример 2
// тестовый пример 3
>
/ * Этот Java-код предоставлен 29AjayKumar * /
# Эффективное решение, чтобы найти
№ из максимального периметра треугольника, который
# может быть сформирован с использованием элементов
# данного массива
# Функция для поиска
# максимальный периметр
for i in range ( 0 , n — 2 ):
if arr[i] + 1 ] + arr[i + 2 ]):
maxi = max (maxi, arr[i] +
arr[i + 1 ] + arr[i + 2 ])
return «Triangle formation is not possible»
return «Maximum Perimeter is: » + str (maxi)
arr1 = [ 6 , 1 , 6 , 5 , 8 , 4 ]
arr2 = [ 2 , 20 , 7 , 55 ,
arr3 = [ 33 , 6 , 20 , 1 , 8 ,
12 , 5 , 55 , 4 , 9 ]
if __name__ = = ‘__main__’ :
# Этот код добавлен
# Прита Упадхяй
// Эффективное решение для поиска
// вне максимального периметра треугольника, который
// может быть сформирован с использованием элементов
// данного массива
// Функция для определения максимального периметра
static void maxPerimeter( int [] arr, int n) <
// сортируем элементы массива
// в обратном порядке
// сортировать (arr, arr + n, больше ());
// цикл через отсортированный массив
// и проверяем, образует ли он
// треугольник или нет.
for ( int i = 0; i
// Проверяем, есть ли arr [i], arr [i + 1]
// и arr [i + 2] образует треугольник
// если он образует треугольник
// это треугольник с
maxi = Math.Max(maxi, arr[i] + arr[i + 1] + arr[i + 2]);
// Если максимальный периметр ненулевой
// затем распечатать его.
Console.WriteLine( «Maximum Perimeter is: » + maxi);
> // иначе треугольник не образуется
Console.WriteLine( «Triangle formation is not possible.» );
// Функция возвращает отсортированный массив по убыванию
static int [] arrRevSort( int [] arr) <
int j = arr.Length — 1;
for ( int i = 0; i
// Программа для водителя
public static void Main() <
// тестовый пример 1
// контрольный пример 2
// тестовый пример 3
>
/ * Этот код Java предоставлен mits * /
// Эффективное решение, чтобы узнать максимум
// треугольник периметра, который может быть сформирован
// используя элементы данного массива
// Функция для определения максимального периметра
function maxPerimeter(& $arr , $n )
// сортируем элементы массива в
// инициализируем максимальный периметр до 0
// цикл через отсортированный массив
// и проверяем, образует ли он
// треугольник или нет.
for ( $i = 0; $i $n — 2; $i ++)
// Проверяем, есть ли arr [i], arr [i + 1]
// и arr [i + 2] образует треугольник
if ( $arr [ $i ] $arr [ $i + 1] +
// если он образует треугольник
// это треугольник с
$maxi = max( $maxi , $arr [ $i ] +
// Если максимальный периметр ненулевой
// затем распечатать его.
echo ( «Maximum Perimeter is: » );
// иначе треугольник не образуется
echo ( «Triangle formation » );
echo ( «is not possible.» );
// тестовый пример 1
$arr1 = array (6, 1, 6, 5, 8, 4);
maxPerimeter( $arr1 , $s );
// контрольный пример 2
$arr2 = array (2, 20, 7, 55, 1,33, 12, 4);
$st = sizeof( $arr2 );
maxPerimeter( $arr2 , $st );
// тестовый пример 3
$arr3 = array (33, 6, 20, 1, 8,
$st1 = sizeof( $arr3 );
maxPerimeter( $arr3 , $st1 );
// Этот код добавлен
// от Shivi_Aggarwal
?>
Выход :
Временная сложность такого подхода составляет O (n * log (n)). Это много времени требуется для сортировки массива.
- Структуры — введение в объектно-ориентированное программирование
- Упражнения на проектирование структуры “Point”
- A: Самая дальняя точка
- B: Центр масс
- C: Диаметр множества
- D: Сортировка
- E: Максимальный периметр
- F: Максимальная площадь
- Упражнения на проектирование структуры “Fraction”
- G: Метод reduce и вывод дроби
- H: Считывание дроби
- I: Сравнения
- J: Сложение
- K: Вычитание
- L: Умножение и деление
- M: Операторы присваивания
- O: Знаки
- P: Преобразование типов
- 💡 Видео
Видео:Площадь треугольника. Как найти площадь треугольника?Скачать

Структуры — введение в объектно-ориентированное программирование
Раньше для хранения данных использовались простые типы данных: числа, строки и т.д. Тем не менее, многие объекты, которые возникают в программировании, нельзя охарактеризовать только одной числовой или строковой величиной. Например, точка на плоскости задается парой действительных чисел (x, y), а данные о человеке можно задавать при помощи нескольких строк (фамилии, имени, отчества) и числового параметра: года рождения.
Поэтому удобным является использование объектов, объединяющих сразу ряд параметров, каждый из которых может фигурировать, как отдельная переменная.
Для этого используются специальные типы данных, которые в языке C называются структурами, а в языке C++ – классами. Например, структура Point , задающая точку на плоскости и содержащая два действительных числа x и y может быть задана следующим образом:
Переменные x и y , входящие в структуру Point , называются полями структуры. Определение структуры дается вне всех функций (и, обычно делается перед объявлением всех функций). Определение структуры обязательно завершается точкой с запятой.
После этого мы можем работать с Point , как с новым типом данных, содержащим два поля: x и y . Примеры создания переменной и массива переменных типа Point :
Чтобы обратиться к полю какой-либо структуры, используется оператор «точка». Его левый операнд – идентификатор переменной типа структура, правый операнд – имя поля. Например, P.x или Arr[i].y .
Например, считать координаты точки, сохранить их в переменной P и вывести на экран расстояние от начала координат до этой точки можно следующим образом:
По сути, величины P.x и P.y являются независимыми переменными, скомбинированными в один объект. С этим объектом можно работать, как с единым целым, например, можно выполнять присваивания вроде Arr[i]=P , можно сохранить набор точек в одном массиве и т.д.
Аналогично, можно определить структуру типа Person для хранения информации о человеке:
Теперь можем работать с данными типа Person :
Полями структур могут быть произвольные типы данных. Можно, например, создать структуру, полями которой будут массивы или другие структуры.
Например, пусть мы хотим определить структуру Circle для определения окружности. Окружность задается центром и радиусом. Радиус – это действительное число (поле Radius типа double ), а центр – это, конечно же, точка, то есть поле Center имеет тип Point . Получили:
Дальше с такими «вложенными» структурами можно работать так:
Видео:КАК НАЙТИ ПЕРИМЕТР ТРЕУГОЛЬНИКА? Примеры | МАТЕМАТИКА 5 классСкачать

Упражнения на проектирование структуры “Point”
Создайте структуру Point , определите для нее конструктор, необходимые арифметические операции, вывод на экран. У структуры Point два поля: x и y .
A: Самая дальняя точка
Программа получает на вход число N, далее координаты N точек. Выведите координаты точки, наиболее удаленной от начала координат.
Для решения этой задачи напишите метод dist , который возвращает расстояние от точки до начала координат.
| Ввод | Вывод |
|---|
B: Центр масс
Выведите координаты центра масс данного множества точек (учтите, что это —два действительных числа).
Определите операции сложения точек, умножения точки на число, деления точки на число.
| Ввод | Вывод |
|---|
C: Диаметр множества
Выведите диаметр данного множества – максимальное расстояние между двумя данными точками.
Для этого удобно определить операцию разности двух точек, возвращающую разность двух радиус-векторов, затем вызвать метод, вычисляющий длину данного радиус-вектора.
| Ввод | Вывод |
|---|
D: Сортировка
Определите для точек оператор сравнения “ sort из файла algorithm .
| Ввод | Вывод |
|---|
E: Максимальный периметр
Среди данных точек найдите три точки, образующие треугольник с наибольшим периметром. Выведите данный периметр.
Для нахождения периметра треугольника напишите отдельную функцию double Perimeter(Point A, Point B, Point C) .
| Ввод | Вывод |
|---|
F: Максимальная площадь
Среди данных точек найдите три точки, образующие треугольник с наибольшей площадью. Выведите данную площадь.
Для нахождения площади треугольника напишите отдельную функцию double Area(Point A, Point B, Point C) .
| Ввод | Вывод |
|---|
Видео:Периметр треугольника. Как найти периметр треугольника?Скачать

Упражнения на проектирование структуры “Fraction”
Структура Fraction должен иметь два поля: числитель a и знаменатель b . Оба поля должны быть типа int .
Для класса Fraction определите конструкторы, которые могут принимать следующие виды параметров:
- Ни одного параметра (в этом случае дробь должна быть равна 0).
- Один параметр типа Fraction .
- Один параметр типа int .
- Два параметра типа int .
- Один параметр типа str , содержащий два целых числа, записанных либо через пробел, либо через дробную черту или одно целое число.
Необходимо определить вывод дроби в формате a/b в каноническом представлении, если же дробь является целым числом, то просто значение этого числа.
G: Метод reduce и вывод дроби
Необходимо реализовать следующую функциональность структуры:
- Метод reduce .
- Конструкторы Fraction() , Fraction(int) , Fraction(int, int) . Конструктор должен вызывать метод reduce .
- Вывод дроби.
Методика тестирования следующая. Проект должен содержать два файла: fraction.h , содержащий описание и реализацию структуры и fraction.cpp , подключающий fraction.h и содержающий функцию main . На проверку сдается только файл fraction.h , после чего проводится его тестирование на соответствие спецификации.
H: Считывание дроби
Реализовать считывание дроби из потока istream , перегрузив оператор считывания >> . При считывании дробь имеет один из двух форматов: либо целое число, либо два целых числа через дробную черту без пробелов, при этом только числитель может иметь знак “-”.
I: Сравнения
Определите операторы , , > , >= , == , != . Сравнения необходимо реализовать для типов int , double , Fraction , при этом значение типа Fraction может быть как правым, так и левым операндом.
J: Сложение
Определите оператор сложения + так, чтобы можно было складывать:
- Две дроби (результатом является Fraction ).
- Дробь и int в любом порядке (результатом является Fraction ).
- Дробь и double в любом порядке (результатом является double ).
K: Вычитание
Определите оператор вычитания.
L: Умножение и деление
Определите операторы умножения и деления.
M: Операторы присваивания
Определите операторы += , -= , *= , /= для случая, когда правый операнд имеет тип Fraction или int .
Пример определения оператора: __pow__ , __rpow__ так, чтобы можно было возводить дроби в степень типа int , float , Fraction , числа типа int и float в степень Fraction . Операция возведения Fraction ** int возвращает Fraction , во всех остальных случаях возвращается float .
Определите операцию __ipow__ для возведения дроби в целочисленную степень.
O: Знаки
Определите операции __pos__ , __neg__ , __abs__ .
P: Преобразование типов
Определите операции __int__ (должна округлять вниз до ближайшего целого), __float__ , __round__ (должна возвращать значение типа float , можно использовать функцию round для величины типа float ). —>
💡 Видео
Геометрия 7 класс (Урок№9 - Треугольник.)Скачать

Что такое периметр. Как найти периметр многоугольника?Скачать

Урок. Как найти периметр треугольника. Математика 2 класс. #учусьсамСкачать

Как найти периметр?Скачать

Как вычислить периметр #геометрия #задача #треугольник #периметрСкачать

Высота, биссектриса, медиана. 7 класс.Скачать

Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать

Периметр равнобедренного треугольникаСкачать

№540. Периметр треугольника CDE равен 55 см. В этот треугольник вписан ромб DMFN так, чтоСкачать

Площадь прямоугольного треугольника. Как найти площадь прямоугольного треугольника?Скачать

Как найти площадь треугольника без формулы?Скачать

№941. Найдите периметр треугольника MNP, если М (4; 0), N(12; -2), В (5; -9).Скачать
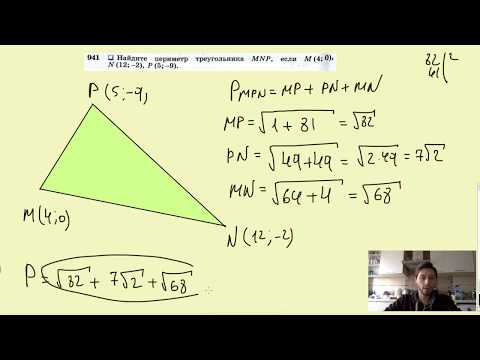
Как найти периметрСкачать

Периметр прямоугольника. Как найти периметр прямоугольника?Скачать

Пример 64. Найти периметр прямоугольного треугольникаСкачать

Задачи на периметр труегольника. Геометрия 7 класс. Две задачи.Скачать

КАК БЫСТРО НАЙТИ ПЕРИМЕТР И ПЛОЩАДЬ ПРЯМОУГОЛЬНИКА И КВАДРАТА ?Скачать
