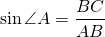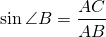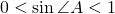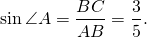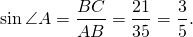Найти синус в треугольнике pdf

Видео:Синус, косинус, тангенс, котангенс за 5 МИНУТСкачать

Синус угла через градусы, минуты и секунды

Видео:Как просто запомнить, что такое sin, cos, tg?! #косинус #синус #тангенс #математика #огэ #егэСкачать

Синус угла через десятичную запись угла

Видео:ТРИГОНОМЕТРИЯ | Синус, Косинус, Тангенс, КотангенсСкачать

Как найти угол зная синус этого угла

У синуса есть обратная тригонометрическая функция — arcsin(y)=x

Пример sin(30°) = 1/2; arcsin(1/2) = 30°

Видео:Находим косинус зная синус, через главное тождество Алгебра 10 классСкачать

Определение синуса

Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.

Синусом угла α называется ордината точки B единичной окружности, полученной при повороте точки P(1;0) на угол α.

Видео:Нахождение стороны прямоугольного треугольникаСкачать

Периодичность синуса

Функция y = sin(x) периодична, с периодом 2π

Видео:СИНУС И КОСИНУС ЛЮБЫХ УГЛОВ | ТригонометрияСкачать

Синус угла в обычном треугольнике

Синус (sin) – это одна из прямых тригонометрических функций. Подробнее о ней можно узнать из нашей статьи Что такое синус.

Видео:ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать

Синус угла в прямоугольном треугольнике

Прежде чем выяснять, как найти синус угла, необходимо определиться с условными обозначениями. Пусть в прямоугольном треугольнике:

• α – острый угол, синус которого нужно найти;
• с – гипотенуза;
• b – прилежащий катет;
• a – противолежащий катет.

Тогда чтобы найти синус острого угла прямоугольного треугольника, достаточно посчитать соотношение длины противолежащего катета к длине гипотенузы: sin(α) = a/c. При этом стоит запомнить, что sin 90° всегда равен 1.

Видео:Синус любого угла. Значения синусов угловСкачать

Синус угла в произвольном треугольнике

Находить синус угла в произвольном треугольнике проще всего с использованием теоремы косинусов (cos): квадрат длины любой стороны равен сумме квадратов длин двух других сторон за минусом их удвоенного произведения на косинус угла между ними.

a² = b² + c² – 2*b*c*cos(α)

Из данной формулы можно найти косинус: cos(α) = (b² + c² – a²)/(2*b*c)

А поскольку для одного и того же угла sin(α)² + cos(α)² = 1 и это константа, то можно вывести формулу для определения синуса:

Более детально нахождение синуса угла с использованием косинуса рассмотрено в нашей статье Как найти синус, если известен косинус.

Что такое синус в треугольнике? Как найти синус острого угла в прямоугольном треугольнике?

Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.

для угла A треугольника ABC

противолежащий катет — это BC.

Соответственно, синус угла A в треугольнике ABC — это

Для угла B треугольника ABC

противолежащим является катет AC.

Соответственно, синус угла B в треугольнике ABC

равен отношению AC к AB:

Таким образом, синус острого угла в прямоугольном треугольнике — это некоторое число, получаемое в результате деления длины противолежащего катета на длину гипотенузы. Длины отрезков выражаются положительными числами, поэтому синус угла треугольника также является положительным числом.

Поскольку длина катета всегда меньше длины гипотенузы, то синус острого угла прямоугольного треугольника — число, меньшее единицы.

Синус любого острого угла прямоугольного треугольника больше нуля, но меньше единицы:

Синус угла треугольника зависит не от длин сторон треугольника, а от отношения этих длин.

1) В треугольнике ABC катет BC=3 см, а гипотенуза AB=5 см.

2) В треугольнике ABC катет BC=21 дм, гипотенуза AB=35 дм.

Длины сторон треугольника изменилось, но отношения длин остались прежними, поэтому и значение синуса угла A не изменилось.

2
Для нахождения синусов углов в произвольном треугольнике, как это ни странно, проще использовать не теорему синусов, а теорему косинусов. Она гласит, что возведенная в квадрат длина любой стороны равна сумме квадратов длин двух других сторон без удвоенного произведения этих длин на косинус угла между ними: А²=В²+С2-2*В*С*cos(α). Из этой теоремы можно вывести формулу для нахождения косинуса: cos(α)=(В²+С²-А²)/(2*В*С) . А поскольку сумма квадратов синуса и косинуса одного и того же угла всегда равна единице, то можно вывести и формулу для нахождения синуса угла α: sin(α)=√(1-(cos(α))²)= √(1-(В²+С²-А²)²/(2*В*С) ²).

Видео:ОГЭ 2021. Фигуры на квадратной решетке.Скачать

Формулы (тождества) синус, косинус, тангенс, котангенс тройного угла

гипотенузу или катеты в прямоугольном треугольнике.

a , b — катеты

c — гипотенуза

α , β — острые углы

Формулы для катета, ( a ):

Формулы для катета, ( b ):

Формулы для гипотенузы, ( c ):

Формулы сторон по теореме Пифагора, ( a , b ):

Вычислить длину неизвестной стороны через любые стороны и углы

b — сторона (основание)

a — равные стороны

α — углы при основании

β — угол образованный равными сторонами

Формулы длины стороны (основания), (b ):

Формулы длины равных сторон , (a):

Вычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу.

a , b , c — стороны произвольного треугольника

α , β , γ — противоположные углы

Формула длины через две стороны и угол (по теореме косинусов), ( a ):

* Внимательно , при подстановке в формулу, для тупого угла ( α >90), cos α принимает отрицательное значение

Формула длины через сторону и два угла (по теореме синусов), ( a):

В прямоугольном треугольнике катеты, являются высотами. Ортоцентр — точка пересечения высот, совпадает с вершиной прямого угла.

H — высота из прямого угла

a, b — катеты

с — гипотенуза

c ₁ , c ₂ — отрезки полученные от деления гипотенузы, высотой

α , β — углы при гипотенузе

Формула длины высоты через стороны, ( H ):

Формула длины высоты через гипотенузу и острые углы, ( H ):

Формула длины высоты через катет и угол, ( H ):

Формула длины высоты через составные отрезки гипотенузы , ( H ):

Высота— перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом).

Высоты треугольника пересекаются в одной точке, которая называется — ортоцентр.

H — высота треугольника

a — сторона, основание

b, c — стороны

β , γ — углы при основании

p — полупериметр, p=(a+b+c)/2

R — радиус описанной окружности

S — площадь треугольника

Формула длины высоты через стороны, ( H ):

Формула длины высоты через сторону и угол, ( H ):

Формула длины высоты через сторону и площадь, ( H ):

Формула длины высоты через стороны и радиус, ( H ):

Медиана, отрезок |CO|, исходящий из вершины прямого угла BCA и делящий гипотенузу c , пополам.

Медиана в прямоугольном треугольнике ( M ), равна, радиусу описанной окружности ( R ).

M — медиана

R — радиус описанной окружности

O — центр описанной окружности

с — гипотенуза

a, b — катеты

α — острый угол CAB

Медиана равна радиусу и половине гипотенузы, ( M ):

Формула длины через катеты, ( M ):

Формула длины через катет и острый угол, ( M ):

Медиана — отрезок |AO|, который выходит из вершины A и делит противолежащею сторону c пополам.

Медиана делит треугольник ABC на два равных по площади треугольника AOC и ABO.

M — медиана, отрезок |AO|

c — сторона на которую ложится медиана

a, b — стороны треугольника

γ — угол CAB

Формула длины медианы через три стороны, ( M ):

Формула длины медианы через две стороны и угол между ними, ( M ):

Формула для вычисления высоты = биссектрисы = медианы.

В равностороннем треугольнике: все высоты, биссектрисы и медианы, равны. Точка их пересечения, является центром вписанной окружности.

L — высота=биссектриса=медиана

a — сторона треугольника

Формула длины высоты, биссектрисы и медианы равностороннего треугольника, ( L ):

Калькулятор — вычислить, найти медиану, биссектрису, высоту

Формулы для вычисления высоты, биссектрисы и медианы.

В равнобедренном треугольнике: высота, биссектриса и медиана, исходящие из угла образованного равными сторонами, один и тот же отрезок.

L — высота = биссектриса = медиана

a — одинаковые стороны треугольника

b — основание

α — равные углы при основании

β — угол образованный равными сторонами

Формулы высоты, биссектрисы и медианы, через сторону и угол, ( L ):

Формула высоты, биссектрисы и медианы, через стороны, ( L ):

1. Найти по формулам длину биссектрисы из прямого угла на гипотенузу:

L — биссектриса, отрезок ME , исходящий из прямого угла (90 град)

a, b — катеты прямоугольного треугольника

с — гипотенуза

α — угол прилежащий к гипотенузе

Формула длины биссектрисы через катеты, ( L ):

Формула длины биссектрисы через гипотенузу и угол, ( L ):

2. Найти по формулам длину биссектрисы из острого угла на катет:

L — биссектриса, отрезок ME , исходящий из острого угла

a, b — катеты прямоугольного треугольника

с — гипотенуза

α , β — углы прилежащие к гипотенузе

Формулы длины биссектрисы через катет и угол, ( L ):

Формула длины биссектрисы через катет и гипотенузу, ( L ):

L — биссектриса, отрезок |OB|, который делит угол ABC пополам

a, b — стороны треугольника

с — сторона на которую опущена биссектриса

d, e — отрезки полученные делением биссектрисы

γ — угол ABC , разделенный биссектрисой пополам

p — полупериметр, p =(a+b+ c )/2

Длина биссектрисы через две стороны и угол, ( L ):

Длина биссектрисы через полупериметр и стороны, ( L ):

Длина биссектрисы через три стороны, ( L ):

Длина биссектрисы через стороны и отрезки d , e , ( L ):

Точка пересечения всех трех биссектрис треугольника ABC, совпадает с центром О, вписанной окружности.

📽️ Видео

🔴 Найдите sin⁡x, если cos⁡x=-√15/4 | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 5 | ШКОЛА ПИФАГОРАСкачать

ОГЭ по математике. В треугольнике АБС известно три стороны. Найди косинус угла. (Вар.8) √ 16Скачать

Треугольники №15, 18. Площадь части треугольника. Высота и основание. Площадь через синус(ОГЭ)Скачать

Математика | Соотношения между сторонами и углами в прямоугольном треугольнике.Скачать

Вывод формул для синуса и косинуса тройного углаСкачать

ПРОБЛЕМНЫЕ ЗАДАЧИ #1 ЕГЭ 2024 с Высотой в Прямоугольном ТреугольникеСкачать

🔴 ТРИГОНОМЕТРИЯ С НУЛЯ (Тригонометрическая Окружность на ЕГЭ 2024 по математике)Скачать

Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

Четырёхугольники №17 из ОГЭ. Sin,cos,tg,ctg табличных углов. Тригонометрия в трапециях.Скачать

Решение прямоугольных треугольниковСкачать

Топография области сосцевидного отростка и треугольника ШипоСкачать