Найти расстояние между точками на окружности (2 видео)

Расстояние между двумя точками онлайн

С помощю этого онлайн калькулятора можно найти расстояние между точками по известным координатам этих точек. Дается решение с пояснениями. Для нахождения расстояния между точками задайте размерность (2-если задача рассматривается в двухмерном пространстве, 3- если задача рассматривается в трехмерном пространстве), введите координаты точек в ячейки и нажмите на кнопку «Решить». Теоретическую часть смотрите ниже.

Содержание

Предупреждение
Расстояние между двумя точками на прямой
Расстояние между двумя точками на плоскости
Расстояние между двумя точками в пространстве
Всё про окружность и круг
Расстояния между двумя точками
Расстояния между двумя точками
Вывод формулы для вычисления расстояния между двумя точками на плоскости
🎦 Видео

Предупреждение

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

Видео:"Парадоксальное" среднее расстояние между точками на окружностиСкачать

Расстояние между двумя точками на прямой

Пусть заданы на оси OX точки A с координатой x_a и B с координатой x_b (Рис.1). Найдем расстояние между точками A и B.

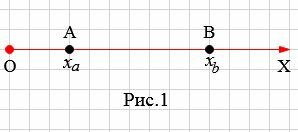Найти расстояние между точками на окружности

Расстояние между точками A и В равно:

( small AB=OB-OA. )

(1)

Поскольку расстояние от O до В равна x_b, а расстояние от O до A равна x_a, получим:

( small AB=x_b-x_a . )

(2)

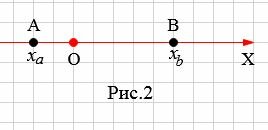На рисунке 2 точки A и В находятся по разные стороны начала координат O. B этом случае рассояние между точками A и B равно:

( small AB=OB+OA. )

(3)

Поскольку координата точки A отрицательна а координата точки B положительна, то (2) можно записать так:

( small AB=x_b+|x_a|=x_b-x_a . )

(4)

На рисунке 3 точки A и В находятся c левой стороны начала координат O.

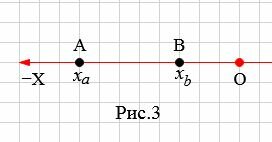B этом случае рассояние между точками A и B равно:

( small AB=OA-OB. )

(5)

Координаты точек A и B отрицательны. Тогда , то (5) можно записать так:

( small AB=|x_a|-|x_b|=x_b-x_a . )

(6)

Из формул (2),(4),(6) следует, что независимо от расположения точек отностительно начала координат рассояние этих точек равна разности координат этих точек, причем от большего значения вычитается меньшее (так как расстояние не может быть отрицательным числом).

Формулы (2),(4),(6) можно записать и так:

( small AB=|x_b-x_a|= |x_a-x_b| . )

(7)

Пример 1. на оси Ox заданы точки ( small A(x_a)=A(-4) ) и ( small B(x_b)=B(7) ) . Найти рассояние между этими точками.

Решение. Для нахождения расстояния между точками A и B воспользуемся формулой (7):

( small AB=|x_b-x_a|= |7-(-4)|=11 . )

(7)

Видео:Уравнение окружности и формула расстояния между точками на плоскостиСкачать

Расстояние между двумя точками на плоскости

Пусть на плоскости задана декартова прямоугольная система координат XOY и пусть на плоскости заданы точки A и B, где A имеет координаты (x_a,y_a), а B имеет координаты (x_b,y_b) (Рис.4).

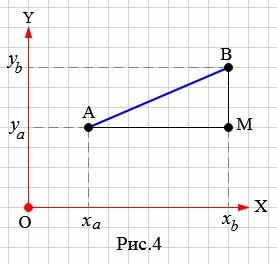Учитывая результаты предыдующего параграфа, можем найти расстояние между точками A и M, а также расстояние между точками B и M:

( small AM=x_b-x_a,;; BM=y_b-y_a. )

(8)

ABM является прямоугольным треугольником, где AB гипотенуза, а AM и BM катеты. Тогда, исходя из теоремы Пифагора, имеем:

( small AB^2=AM^2+BM^2. )

Тогда, учитывая (8), получим:

( small AB^2=AM^2+BM^2=(x_b-x_a)^2+(y_b-y_a)^2. )

( small AB=sqrt . )

(9)

Пример 2. На плоскости, в декартовой прямоугольной системе координат XOY заданы точки ( small A(x_a; y_a)=A(-6;3) ) и ( small B(x_b, y_b)=B(11,-4). ) . Найти рассояние между этими точками.

Решение. Для нахождения расстояния между точками A и B воспользуемся формулой (9). Подставляя координаты точек A и B в формулу (9), получим:

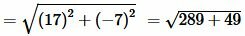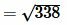Ответ: .

Видео:Расстояние между точкамиСкачать

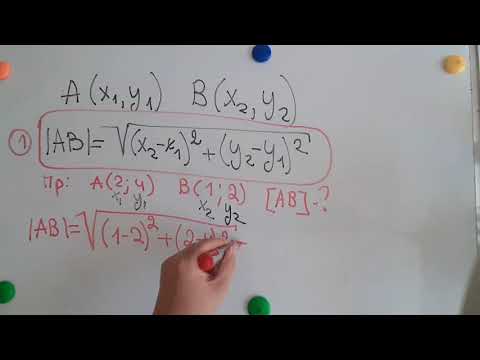
Расстояние между двумя точками в пространстве

Рассмотрим в пространстве, в декартовой прямоугольной системе координат точки A и B, где A имеет координаты (x_a,y_a,z_a), а B имеет координаты (x_b,y_b,z_b) (Рис.5).

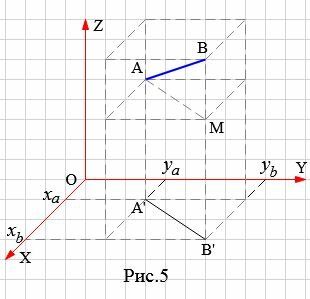AB является диагональю параллелепипеда, грани которго параллельны координатным плоскостьям и проходят через точки A и B. Но AB является гипотенузой прямоугольного треугольника AMB, а AM и BM являются катетами этого прямоугольного треугольника. Тогда, по теореме Пифагора, имеем:

( small AB^2=AM^2+BM^2. )

(10)

Учитывая, что BM равно разности третьих координат точек B и A, получим:

( small BM=z_b-z_a. )

Из предыдующего параграфа следует, что:

( small A’B’^2=(x_b-x_a)^2+(y_b-y_a)^2. )

(11)

Но AM=A’B’. Тогда из (10) и (11) следует:

( small AB^2=AM^2+BM^2=A’B’^2+BM^2 ) ( small =(x_b-x_a)^2+(y_b-y_a)^2+(z_b-z_a)^2. )

( small AB= sqrt. )

(12)

Пример 3. В пространстве задана декартова прямоугольная система координат XOY и точки ( small A(x_a; y_a ; z_a)=A(5;1;0) ) и ( small B(x_b, y_b, z_b)=B(-8,-4;21). ) Найти рассояние между этими точками.

Решение. Для нахождения расстояния между точками A и B воспользуемся формулой (12). Подставляя координаты точек A и B в формулу (12), получим:

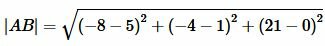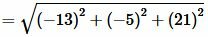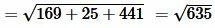Ответ: .

Видео:Расстояние между точками по координатам.Скачать

Всё про окружность и круг

Окружность — это геометрическое место точек плоскости, равноудаленных от некоторой заданной точки (центра окружности). Расстояние между любой точкой окружности и ее центром называется радиусом окружности (радиус обозначают буквой R).
Значит, окружность — это линия на плоскости, каждая точка которой расположена на одинаковом расстоянии от центра окружности.

Кругом называется часть плоскости, ограниченная окружностью и включающая ее центр.

Отрезок, соединяющий две точки окружности, называется хордой. Хорда, проходящая через центр окружности, представляет собой диаметр. Диаметр окружности равен ее удвоенному радиусу: D = 2R.

Точка пересечения двух хорд делит каждую хорду на отрезки, произведение которых одинаково: a1a2 = b1b2

Касательная к окружности всегда перпендикулярна радиусу, проведенному в точку касания.

Отрезки касательных к окружности, проведенные из одной точки, равны: AB = AC, центр окружности лежит на биссектрисе угла BAC.

Квадрат касательной равен произведению секущей на ее внешнюю часть

Центральный угол — это угол, вершина которого совпадает с центром окружности.

Дугой называется часть окружности, заключенная между двумя точками.

Мерой дуги (в градусах или радианах) является центральный угол, опирающийся на данную дугу.

Вписанный угол это угол, вершина которого лежит на окружности, а cтороны угла пересекают ее.

Вписанный угол равен половине центрального, если оба угла опираются на одну и ту же дугу окружности.
Внутренние углы, опирающиеся на одну и ту же дугу, равны.

Сектором круга называется геометрическая фигура, ограниченная двумя радиусами и дугой, на которую опираются данные радиусы.

Периметр сектора: P = s + 2R.

Площадь сектора: S = Rs/2 = ПR 2 а/360°.

Сегментом круга называется геометрическая фигура, ограниченная хордой и стягиваемой ею дугой.

Видео:Amr и булавки (Геометрия: Окружности, Расстояние между точками)Скачать

Расстояния между двумя точками

На данной странице калькулятор поможет рассчитать расстояние между двумя точками онлайн в плоскости и пространстве. Для расчета задайте координаты.

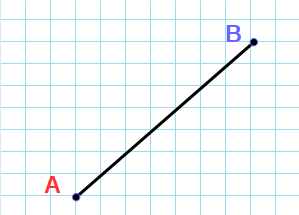
Расстояние между двумя точками — это длина отрезка, которая соединяет эти точки.

Расстояния между двумя точками

Формула вычисления расстояния между двумя точками A(x_a; y_a) и B(x_b; y_b) на плоскости:

Формула вычисления расстояния между двумя точками A(x_a; y_a; z_a) и B(x_b; y_b; z_b) в пространстве:

Вывод формулы для вычисления расстояния между двумя точками на плоскости

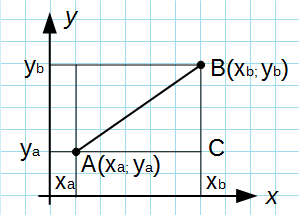
Из точек A и B опустим перпендикуляры на оси координат x и y.

Рассмотрим прямоугольный треугольник ∆ABC. Катеты этого треугольника равны:

Спомощью теоремы Пифагора, вычислим длину отрезка AB:

Подставив в это выражение длины отрезков AC и BC, выраженные через координаты точек A и B, получим формулу для вычисления расстояния между точками на плоскости.

Формула для вычисления расстояния между двумя точками в пространстве выводится аналогично.