Найти расстояние между плоскостью и параллельной ей прямой

В этой статье дано определение расстояния между параллельными прямой и плоскостью, приведена теория, необходимая для нахождения расстояния между прямой и параллельной ей плоскостью методом координат, а также подробно разобраны решения характерных примеров и задач.

Навигация по странице.

Видео:19. Расстояние между параллельными прямыми Расстояние между скрещивающимися прямымиСкачать

Расстояние между параллельными прямой и плоскостью – определение.

Расстояние между прямой и параллельной ей плоскостью определяется через расстояние от точки до плоскости.

Расстояние между параллельными прямой и плоскостью – это расстояние от любой точки заданной прямой до заданной плоскости.

Рассмотрим прямую a и параллельную ей плоскость . Отметим на прямой a точку M₁ и опустим перпендикуляр M₁H₁ из этой точки на плоскость . Длина перпендикуляра M₁H₁ есть расстояние между заданными параллельными прямой и плоскостью.

Озвученное определение расстояния между параллельными прямой и плоскостью тесно связано со следующей теоремой.

Если прямая a параллельна плоскости , то все точки прямой a равноудалены от плоскости .

Проведем через произвольную точку прямой a плоскость параллельно плоскости . Прямая a при таком построении плоскости лежит в этой плоскости (если бы это было не так, то прямая a пересекала бы плоскость , а, значит, пересекала бы и плоскость в силу параллельности плоскостей и ). В статье расстояние между параллельными плоскостями мы доказали теорему о том, что все точки одной из параллельных плоскостей находятся на одинаковом расстоянии от другой плоскости. Следовательно, все точки прямой a , которая лежит в плоскости , параллельной плоскости , равноудалены от плоскости , что и требовалось доказать.

Видео:10 класс, 19 урок, Расстояние от точки до плоскостиСкачать

Нахождение расстояния между прямой и параллельной ей плоскостью – теория, примеры, решения.

Расстояние между параллельными прямой и плоскостью обычно находится с помощью методов, изученных на уроках геометрии в 10-11 классах, — с использованием теоремы Пифагора, признаков равенства или подобия треугольников, определения синуса, косинуса или тангенса угла и т.п.

Когда в трехмерном пространстве введена прямоугольная система координат и требуется вычислить расстояние между заданными параллельными прямой и плоскостью, то применяется метод координат. Сейчас мы его подробно разберем, после чего рассмотрим решения нескольких примеров.

Поставим перед собой следующую задачу.

Пусть в трехмерном пространстве зафиксирована прямоугольная система координат Oxyz , в ней заданы параллельные прямая a и плоскость , и требуется найти расстояние между прямой a и плоскостью .

Решение этой задачи будем строить на основе определения расстояния между прямой и параллельной ей плоскостью.

Искомое расстояние между заданными параллельными прямой и плоскостью по определению равно расстоянию от точки М₁ , лежащей на прямой a , до плоскости . Если мы определим координаты некоторой точки М₁ , лежащей на прямой a , и получим нормальное уравнение плоскости в виде , то мы сможем вычислить искомое расстояние , применив формулу (эта формула была получена в разделе нахождение расстояния от точки до плоскости).

Итак, алгоритм, позволяющий найти расстояние между параллельными прямой a и плоскостью , таков:

• находим координаты некоторой точки М₁ , лежащей на заданной прямой a (это легко сделать, если знать основные виды уравнений прямой в пространстве);
• получаем нормальное уравнение заданной плоскости вида (для этого нужно знать основные виды уравнения плоскости и при необходимости уметь приводить уравнение плоскости к нормальному виду);
• вычисляем требуемое расстояние между прямой a и параллельной ей плоскостью по формуле .

Воспользуемся полученным алгоритмом при решении задач, в которых требуется вычислить расстояние между параллельными прямой и плоскостью.

Найдите расстояние между параллельными прямой и плоскостью .

Очевидно, точка лежит на прямой, которую определяют канонические уравнения прямой в пространстве .

Получим нормальное уравнение плоскости . Для этого приведем заданное общее уравнение плоскости к нормальному виду: вычисляем нормирующий множитель , умножаем на него обе части заданного общего уравнения плоскости .

Осталось вычислить требуемое расстояние между заданными параллельными прямой и плоскостью как расстояние от точки до плоскости :

Найдите расстояние между прямой и параллельной ей плоскостью .

В рассматриваемой задаче прямая задана уравнениями двух пересекающихся плоскостей. Найдем координаты некоторой точки М₁ , лежащей на этой прямой. Координаты точки М₁ должны удовлетворять уравнениям прямой, то есть, — частное решение системы линейных уравнений . Найдем частное решение этой системы (при необходимости смотрите статью решение систем линейных уравнений). Приняв , приходим к системе уравнений , откуда находим . То есть, имеем .

Теперь получим нормальное уравнение плоскости, которую задает уравнение плоскости в отрезках вида . Для этого переходим к общему уравнению плоскости . Полученное общее уравнение плоскости уже является нормальным уравнением плоскости и его не нужно приводить к нормальному виду.

Осталось вычислить расстояние от точки до плоскости , которое равно искомому расстоянию между параллельными прямой и плоскостью: .

Видео:Расстояние между параллельными плоскостямиСкачать

Геометрия

Лучшие условия по продуктам Тинькофф по этой ссылке

Дарим 500 ₽ на баланс сим-карты и 1000 ₽ при сохранении номера

. 500 руб. на счет при заказе сим-карты по этой ссылке

Лучшие условия по продуктам
ТИНЬКОФФ по данной ссылке

План урока:

Видео:Расстояние между параллельными прямымиСкачать

Понятие перпендикуляра

Пусть есть некоторая плоскость α и точка М в пространстве, не лежащая на α. Проведем через М прямую, перпендикулярную α. Она пересечет α в какой-нибудь точке К. Отрезок МК именуют перпендикуляром к плоскости α.

Если через М мы проведем ещё одну прямую, пересекающую α, то она пересечет α в какой-нибудь точке Н. В результате мы получим прямоугольный ∆МНК:

Запомним некоторые геометрические термины. В таком построении:

• отрезок МН – это наклонная;
• отрезок НК – это проекция наклонной, или просто проекция;
• К – основание перпендикуляра;
• Н – основание наклонной.

Заметим, что в ∆МНК отрезок МН – это гипотенуза, а МК – это катет. Напомним, что катет всегда меньше гипотенузы. Отсюда вытекает вывод – длина перпендикуляра всегда меньше длины наклонной (конечно, если они проведены из одной точки).

Это значит, что из всех отрезков, которыми можно соединить точку и плоскость, именно перпендикуляр будет кратчайшим. Поэтому его называют расстоянием между точкой и плоскостью.

Видео:7. Расстояние от точки до плоскости (вывод формулы примеры)Скачать

Расстояния между плоскостями и прямыми

Докажем довольно очевидный факт:

Действительно, пусть α и β – параллельные плоскости. Выберем на α произвольные точки М и Р, а далее опустим перпендикуляры из точек М и Р на β, которые пересекут β в точках Н и К соответственно:

Так как МН и РК перпендикулярны плоскости α, то они параллельны. Но также и α||β. Тогда, по теореме 12 из этого урока, отрезки МН и РК одинаковы, ч. т. д.

Этот факт позволяет ввести понятия расстояния между параллельными плоскостями.

Уточним, что если плоскости пересекаются, то расстояние между ними не может быть определено.

Далее рассмотрим случай с плоскостью α и параллельной ей прямой m. Оказывается, и в этом случае точки прямой равноудалены от плоскости.

Действительно, отметим на m произвольную точку К. Далее через K проведем такую плоскость β, что α||β. Так как точки β равноудалены от α, то нам достаточно показать, что m будет полностью принадлежать β:

Так как m и β уже имеют общую точку K, то они m либо пересекает β, либо лежит в ней. Будем рассуждать от противного и предположим, что m и β пересекаются. Так как m||α, то в α можно построить прямую n, параллельную m. Если m пересекает β, то и nтакже должна ее пересекать (по теореме 3 из этого урока). Но если n пересекает β, то точка их пересечения будет одновременно принадлежать и β, и α. То есть у этих плоскостей будет общая точка. Но α и β параллельны и потому не могут иметь общих точек. Значит, на самом деле m и β НЕ пересекаются. Остается один вариант – m принадлежит β, ч. т. д.

Из этой теоремы вытекает понятие расстояния между прямой и плоскостью.

Уточним, что если плоскость и прямая не параллельны, то расстояние между ними определить нельзя.

Осталось понять, как определять расстояние между прямыми в пространстве. Для параллельных прямых определение расстояния известно ещё из курса планиметрии. Естественно, что для пересекающихся прямых расстояние определить невозможно. Остается только случай скрещивающихся прямых.

Пусть прямые m и n скрещиваются. Тогда через n можно построить плоскость α, параллельную m. И наоборот, через m возможно провести плоскость β, параллельную n:

Далее опустим из какой-нибудь точки m перпендикуляр на α. Обозначим этот перпендикуляр как р. Тогда через пересекающиеся прямые m и р можно провести единственную плоскость γ:

Заметим, что плоскости α и γ обязательно пересекутся по некоторой прямой m’, причем m’||m. Действительно, m’ и m не могут скрещиваться, ведь они находятся в одной плоскости γ. Не могут они и пересекаться, ведь в противном случае точка их пересечения была бы общей для m и α, а они параллельны и общих точек не имеют.

Также заметим, что прямые n и m’ пересекаются, ведь они располагаются в одной плоскости α. Параллельными они быть не могут, ведь тогда по свойству транзитивности параллельности получилось бы, что и n||m, а это не так. Обозначим точку пересечения n и m’ буквой K.

Далее через K в плоскости γ проведем прямую р’, параллельную р:

Теперь начнем рассуждения. Если р⊥α, то также р⊥m’. Так как р’||р, то и р’⊥m’, ведь прямая, перпендикулярная одной из параллельных прямых, будет перпендикулярна и второй прямой. По этому же правилу из того факта, что m’||m и р’⊥m’ вытекает, что и m⊥р’. Наконец, если р⊥α, то р⊥n. Для ясности отметим все найденные нами прямые углы на рисунке:

В итоге получилось, что отрезок HK перпендикулярен и n, и m. По этой причине его называют общим перпендикуляром к прямым n и m. Именно он и считается расстоянием между скрещивающимися прямыми m и n.

Отдельно отметим, что HK – это ещё и общий перпендикуляр к α и β. Понятно, что так как р⊥α и р’||р, то и р’⊥α, то есть HK – перпендикуляр к α.

Теперь через точку H проведем прямую n’, параллельную n. Так как β||n, то n’ будет находиться в β (по теор. 6 в этом уроке).

Раз n||n’ и р’⊥n, то и р’⊥n’. Тогда получается, что в β есть сразу две пересекающихся прямых (это m и n’), которые перпендикулярны р’. Поэтому можно утверждать, что р’⊥β, то есть HK– перпендикуляр к β.

Отсюда сразу вытекает ещё один важный вывод – плоскости α и β параллельны, так как имеют общий перпендикуляр.

Итак, мы показали, что общий перпендикуляр можно построить для любых двух скрещивающихся прямых. Но можно построить ещё один такой перпендикуляр? Нельзя, и это можно показать.

Сначала заметим, что второй перпендикуляр нельзя провести через точку К, ведь в таком случае получалось бы, что к m проведены два различных перпендикуляра из одной и той же точки, что невозможно. Аналогично перпендикуляр не может проходить и через Н.

Предположим тогда, что второй перпендикуляр проходит через точки С и D, причем С находится на m, а D находится на n. То есть CD⊥m и СD⊥n:

Проведем через С прямую n’’, параллельную n. Раз СD⊥n и n||n’’, то и СD⊥n’’. При этом n’’ находится в β (это доказывается также, как и в случае с n’). Тогда получается, что в β есть две прямые, n’’ и m, каждая из которых перпендикулярна СD, и при этом n’’ и m пересекаются. Тогда CD⊥β. Из этого вытекает, что СD и HK параллельны, а потому через них можно провести плоскость δ. Этой плоскости будут принадлежать точки С, H, К и D. Но тогда в этой плоскости должны находиться прямые m и n, ведь они имеют с ней по две общих точки. Но m и n – скрещивающиеся прямые, то есть они никак не могут находиться в одной плоскости. Это противоречие означает, что второй общий перпендикуляр CD не существует.

Итак, из всех наших рассуждений мы можем сделать следующие выводы:

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Теорема о трех перпендикулярах

Сформулируем важное утверждение, которое называют теоремой о трех перпендикулярах.

Проиллюстрируем теорему с помощью картинки:

Доказательство этой теоремы очень простое. Так как МК⊥α, то также МК⊥m. Теперь рассмотрим расположение плоскости МНК и прямой m. МК⊥m и HK⊥m. Тогда по признаку перпендикулярности можно утверждать, что m перпендикулярна всей плоскости HM, то есть каждой находящейся в ней прямой. В частности, m⊥HK, ч. т. д.

Оказывается, верно и обратное утверждение (так называемая обратная теорема о трех перпендикулярах):

Доказательство аналогично предыдущему. Так как m⊥MH и m⊥MK, то m⊥HMK. Отсюда вытекает, что и m⊥HK.

Видео:Определение кратчайшего расстояние между скрещивающимися прямыми методом замены плоскостей проекцииСкачать

Угол между прямой и плоскостью

Проекция наклонной позволяет ввести такое понятие, как угол между прямой и плоскостью.

Пусть надо определить угол между прямой HM и плоскостью α:

Здесь надо просто построить перпендикуляр МК. В результате появится отрезок HK– проекция HM на α. Тогда угол между HM и HK, то есть ∠MHK, как раз и будет углом между HM и α.

Однако не всегда таким образом можно построить проекцию прямой. Проблемы возникнут, если прямая либо параллельна, либо перпендикулярна плоскости. В таких случаях используются такие правила:

Видео:Параллельность прямой и плоскости. 10 класс.Скачать

Задачи на перпендикуляры, наклонные, расстояния

Рассмотрим несколько задач, в каждой из которых рассматривается куб АВСDEFGH. При этом предполагается, что ребро такого куба имеет длину, равную единице.

Задание. В кубе АВСDEFGH найдите расстояние между точкой А и гранью CDHG:

Решение. Ребро AD перпендикулярно грани DH (так как AD⊥DH и AD⊥CD). Поэтому как раз АD и является расстоянием между А и СDHG. Значит, оно равно единице.

Примечание. Для решения следующих задач запомним, что ребро DH перпендикулярно грани АВСD. Вообще в кубе все ребра, пересекающиеся с гранями, перпендикулярны таким граням.

Задание. Найдите в кубе расстояние между вершиной А и плоскостью BDH:

Решение. Проведем на грани АВСD перпендикуляр АК из А к прямой BD:

Докажем, что АК – перпендикуляр в BDH. Для этого надо найти две прямые в BDH, перпендикулярные АК. Первая такая прямая – это BD (мы специально провели АК⊥BD). Вторая такая прямая – это DH. Действительно, DH перпендикулярна всей грани АВСD, а значит, и прямой АК.

Теперь найдем длину АК. Ее можно вычислить из прямоугольного ∆АКD. В нём ∠ADB =45°, ведь это угол между стороной квадрата АВСD и его диагональю.

Найти АК можно с помощью тригонометрии в ∆АКD:

Задание. Найдите расстояние от H до плоскости EDG:

Решение. Обозначим середину отрезка ЕD буквой М.Далее в ∆МНG опустим высоту из НК на сторону MG:

Попытаемся доказать, что HK – это перпендикуляр к EDG. Заметим, что ∆HDG и ∆EHG равны, ведь у них одинаковую длину имеют ребра DH, EH, ребро GH – общее, а ∠DHG и ∠EHG прямые. Тогда одинаковы отрезки EG и DG. Это означает, что ∆EGD – равнобедренный.

В ∆EGDMG– это медиана. Так как ∆EGD – равнобедренный, то MG одновременно ещё и высота, поэтому MD⊥MG.

Аналогично ∆EHD– равнобедренный (EH = HD), а потому MH в нем – и медиана, и высота. Поэтому MD⊥MH.

Получили, что MD перпендикулярен и MH, и MG, то есть двум прямым в плоскости MHG. Тогда MD перпендикулярен всей плоскости MHG, и, в частности, отрезку HK: HK⊥MD.

Но также MD⊥MG. Получается, KH перпендикулярен двум прямым в плоскости EDG, и потому он является перпендикуляром к плоскости EDG. Значит, именно его длину нам и надо найти.

Рассмотрим ∆MDH. Он прямоугольный, а ∠MDH = 45° (угол между стороной и диагональю квадрата). Тогда длину MH можно найти так:

Так как ребро GH перпендикулярно грани АЕНD, то ∆MHG – прямоугольный. Тогда по теореме Пифагора можно найти MG:

Далее можно найти HK разными способами, но проще воспользоваться подобием ∆MHG и ∆MKH. Они оба – прямоугольные, и у них есть общий угол ∠KMH, этого достаточно для подобия треугольников. Записываем пропорцию:

Здесь слева записано отношение сторон, лежащих против ∠KMH, а справа – отношение сторон, лежащих против прямых углов (то есть отношение гипотенуз). Используем пропорцию дальше:

Задание. Найдите расстояние между прямыми ВС и DH:

Решение. ВС и DH – скрещивающиеся. Надо найти общий перпендикуляр к ним. В данном случае он очевиден – это отрезок CD. Действительно, CD⊥ВС как стороны квадрата АВСD, но и DH⊥CD как стороны в другом квадрате, СDHG.. Длина же ребра CD равна единице, ведь у куба все ребра одинаковы.

Задание. Каково расстояние между прямыми ВС и DG:

Решение.На грани СDHG опустим из С перпендикуляр СК на диагональ GD:

Будет ли СК являться расстоянием между ВС и DG? Ясно, что СК⊥DG. При этом ребро ВС перпендикулярно грани СGHD, так как ВС⊥СG и ВС⊥СD. Значит, также ВС⊥СК. То есть СК – общий перпендикуляр к ВС и DG, и по определению как раз и является искомым расстоянием.

Длину СК найдем из прямоугольного ∆СKG. ∠СGK составляет 45°, ведь это угол между диагональю DG и стороной квадрата СG. Тогда можно записать:

Задание. Найдите расстояние между ребрами АВ и HG:

Решение. Здесь ребра АВ и HG параллельны, так как каждая их них параллельна ребру CD. Проведем отрезок АН. Так как и АВ, и HG перпендикулярны грани АЕНD, то эти ребра одновременно перпендикулярны и АН. То есть АН – общий перпендикуляр к АВ и HG, и поэтому именно его длину и надо найти.

Сделать это можно из прямоугольного ∆АНD, в котором ∠НАD составляет 45°:

Задание. Чему равно расстояние между ребром AB и диагональю FD:

Решение. Пусть А₁, D₁, H₁ и Е₁ – середины ребер АВ, DC, HG, и EF соответственно. Проведем через А₁, D₁, H₁ плоскость. Диагональ FD пересечет ее в какой-нибудь точке К:

Сначала покажем, что плоскости α и ADH (то есть нижняя грань) параллельны.

Заметим, что в четырехугольнике АА₁D₁D стороны АА₁ и DD₁ параллельны (ведь они лежат на сторонах квадрата АВСD) и одинаковы (ведь они составляют половину от длины ребер АВ и CD, то есть имеют длину 0,5). Тогда АА₁D₁D – параллелограмм. Более того, раз у него есть прямые углы ∠А₁АDи ∠АDD₁, то можно утверждать, что АА₁D₁D – прямоугольник. Тогда АD||A₁D₁. Аналогично можно показать, что DHH₁D₁ – прямоугольник, и DH||D₁H₁.

Далее можно действовать разными способами. Первый способ – это использование признака параллельности плоскостей (теорема 9 из этого урока). Так как в α есть пересекающиеся прямые А₁D₁и D₁H₁, а в плоскости ADH находятся прямые AD и DH, и АD||A₁D₁, и DH||D₁H₁, то по этому признаку α||ADH.

Однако, если этот признак вдруг оказался «забыт», то можно использовать отрезок DD₁. Он перпендикулярен и грани ADHE, и плоскости α, ведь в каждой из них есть по две прямых, перпендикулярных ему. Это AD и DH на грани ADHE и A₁D₁и D₁H₁ в α. Тогда α и ADH перпендикулярны одной и той же прямой, а потому они параллельны. Так или иначе, мы выяснили, что α||ADH.

Отсюда вытекает, что α должна проходить через середину Е₁. Действительно, расстояние между параллельными плоскостями не зависит от выбора точек измерения. В данном случае оно равно отрезку АА₁, то есть 0,5. Но FE– это также общий перпендикуляр к α и ADH. Значит, α пересекает FE в точке, находящейся на расстоянии 0,5 от Е. А это как раз и есть середина FE, то есть точка Е₁.

Далее докажем, что точка К, в которой прямая FD пересекает α – это середина отрезка Е₁D₁. Для этого удобно отдельно показать плоскость, проходящую через параллельные ребра FE и CD, то есть четырехугольник FEDC:

Заметим, так как ребра FE и CD перпендикулярны верхней и нижней грани, то они перпендикулярны и отрезкам FC и ED, то есть FEDC прямоугольник. Тогда FC||ED, и ∠Е₁FD = ∠D₁DF (накрест лежащие углы при секущей FD). ∠FKE₁ и ∠DKD₁ одинаковы уже как вертикальные углы. Тогда ∆FKE₁ и ∆DKD₁ подобны по 2 углам. Но отрезки FE₁ и DD₁ одинаковы как половины равных ребер FE и CD. Получается, что ∆FKE₁ и ∆DKD₁ равны, и поэтому Е₁К = KD₁. Это и значит, что К – середина Е₁D₁.

Также отметим, что Е₁D₁ – диагональ в четырехугольнике А₁Е₁Н₁D₁. Докажем, что А₁Е₁Н₁D – это квадрат. Ранее мы уже показали, что АА₁D₁D и DHH₁D₁ – прямоугольники. Аналогично можно продемонстрировать, что прямоугольниками являются также АА₁Е₁Е и ЕЕ₁Н₁Н. Из этого вытекает равенство сторон:

То есть в А₁Е₁Н₁D₁ все стороны одинаковы, и эта фигура – ромб. Теперь надо показать, что и углы в этом четырехугольнике составляют 90°. Продемонстрируем это на примере ∠А₁D₁H₁. AD⊥CDHG и AD||A₁D₁, поэтому А₁D₁⊥CDHG. Значит, также А₁D перпендикулярна любой прямой на грани CDHG, в том числе и D₁H₁. То есть ∠А₁D₁H₁ = 90°. Но если в ромбе хотя бы один угол прямой, то он является квадратом.

Итак, мы выяснили, что А₁Е₁Н₁D₁ – квадрат, а К – середина его диагонали Е₁D₁. Получается, что К – точка пересечения диагоналей квадрата А₁Е₁Н₁D₁, ведь эта точка пересечения как раз делит диагонали пополам.

Теперь мы можем наконец доказать, что А₁К – это и есть искомое расстояние. Действительно, так как АВ – перпендикуляр к α, та А₁К принадлежит α, то А₁К⊥АВ. Но как же доказать, что А₁К⊥FD. Здесь поможет теорема о трех перпендикулярах. Е₁К – это проекция FK на α, и Е₁К⊥А₁К, ведь диагонали квадрата пересекаются под прямым углом. Раз отрезок А₁К перпендикулярен проекции, то он перпендикулярен и самой наклонной, то есть А₁К⊥FK.

Осталось лишь вычислить длину А₁К. Для этого по аналогии с предыдущими задачами используем прямоугольный∆А₁Е₁К, в котором ∠А₁Е₁К = 45°:

Отвлечемся от куба и рассмотрим другую задачу.

Задание. В ∆АВС вписана окружность. Через центр этой окружности (точку О) проведена прямая ОН, причем она перпендикулярна плоскости АВС. Верно ли, что точка Н находится на одинаковом расстоянии от прямых АВ, АС и ВС?

Решение. Пусть N, K и M – точки касания окружности и сторон АВ, АС и ВС соответственно. Тогда ОN, OK и OM– радиусы, а они должны быть перпендикулярны касательным, то есть

Заметим, что ОN, OK и OM – это также проекции прямых HN, HK и HM соответственно. Раз отрезки АВ, АС и ВС перпендикулярны этим проекциям, то они должны быть перпендикулярны и наклонным:

Это значит, что HN, HK и HM– это расстояния от H до сторон ∆АВС. Осталось показать, что они одинаковы. Это можно сделать с помощью ∆HON, ∆HOK и ∆HOM. Они все прямоугольные, причем катет OH– общий, а катеты ON, OM и OK одинаковы как радиусы одной окружности. Отсюда вытекает вывод, что эти треугольники равны, то есть одинаковы и их гипотенузы HN, HKи HM, ч. т. д.

Теперь снова вернемся к кубу, чтобы на практике научиться определять угол между прямой и плоскостью.

Задание. Найдите угол между ребром куба BD и гранью СDHG:

Решение. ВС – это перпендикуляр к грани СDHG, поэтому CD– проекция BD на грань СDHG. Тогда нам надо найти ∠BDC. Он составляет 45°, так как это угол между стороной и диагональю квадрата АВСD:

Задание. Вычислите угол между ребром CD и плоскостью BDHF:

Решение. Нам надо из С опустить перпендикуляр на BDHF. Несложно догадаться, что для этого надо на грани ABCD опустить перпендикуляр СК на диагональ BD:

Действительно, СK⊥BD. Надо найти ещё одну прямую в BDHF, перпендикулярную СК. И такой прямой может быть BF. Так как BF перпендикулярна всей грани АВСD, то она обязательно перпендикулярна и СК. Получаем, что СК⊥BF и CK⊥BD, и тогда СK⊥BDHF.

Если СK– перпендикуляр, то KD – это проекция СD. Тогда искомый нами угол – это ∠СDK. Он равен 45°, ведь BD – диагональ квадрата АВСD, а CD – его сторона.

Задание. Чему равен угол между прямой BD и плоскостью ABGH:

Решение. На нижней грани АЕНD опустим на АН перпендикуляр DK:

Заметим, что ребро АВ перпендикулярно грани АЕНD, поэтому KD⊥АВ. Но также KD⊥AH (мы специально построили так KD). Тогда можно утверждать, что KD – это перпендикуляр ко всей плоскости АВGH.

В таком случае BK – это проекция BD на AB. Значит, нам необходимо вычислить ∠DBK. Его можно найти из прямоугольного ∆DBK, но сперва надо вычислить длины сторон KD и BD.

ВD найдем из прямоугольного ∆ABD:

Теперь мы можем найти ∠DBK, а точнее его синус, из ∆DBK:

По таблице синусов легко определить, что ∠DBK = 30°.

В ходе сегодняшнего урока мы узнали о перпендикуляре к плоскости. Перпендикуляры используются для определения расстояний в стереометрии, а также угла между прямой и плоскостью.

Видео:Определение расстояние между параллельными прямыми (Способ замены плоскостей проекции).Скачать

Расстояние между прямой и параллельной ей плоскостью: определение и примеры нахождения

В статье ниже мы найдем определение, что же представляет собой расстояние между прямой и плоскостью, параллельными друг другу; разберем способ определить это расстояние и применим полученный навык в решении конкретных задач.

Видео:Параллельность прямых и плоскостей в пространстве. Практическая часть - решение задачи. 10 класс.Скачать

Расстояние между прямой и параллельной ей плоскостью: определение

Расстояние между прямой и параллельной ей плоскостью – это расстояние от любой точки заданной прямой до заданной плоскости.

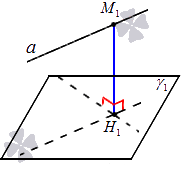
Пусть нам даны прямая a и плоскость ϒ 1 , ей параллельная. Используем некоторую точку М 1 , принадлежащую прямой a : проведем перпендикуляр из этой точки на заданную плоскость. Основание перпендикуляра на плоскости обозначим как Н 1 . Длина перпендикуляра М 1 Н 1 и будет являться расстоянием между исходными параллельными прямой и плоскостью.

Указанное определение имеет тесную взаимосвязь со следующей теоремой.

Когда прямая a параллельна плоскости ϒ 1 , все точки прямой a находятся на одинаковом расстоянии от плоскости ϒ 1 .

Используем любую произвольную точку на прямой a – проведем через нее плоскость ϒ 2 , параллельную заданной плоскости ϒ 1 . В таком построении прямая а принадлежит плоскости ϒ 2 (в ином случае прямая а пересекала бы эту плоскость, а, следовательно, пересекала бы и плоскость ϒ 1 , что противоречит исходному условию). В статье, которая разбирает тему расстояния между параллельными плоскостями, мы доказали теорему о том, что все точки одной из параллельных плоскостей равноудалены от точек другой плоскости. Таким образом, все точки прямой a , принадлежащей плоскости ϒ 2 (в свою очередь, параллельной плоскости ϒ 1 ) находятся на одинаковом расстоянии от плоскости ϒ 1 . Что и требовалось доказать.

Видео:Геометрия 7 класс (Урок№26 - Расстояние от точки до прямой. Расстояние между параллельными прямыми.)Скачать

Нахождение расстояния между параллельными прямой и плоскостью

Искомое расстояние между параллельными прямой и плоскостью обычно находится с использованием теоремы Пифагора, признаков равенства или подобия треугольников и пр.

Если же в трехмерном пространстве задана прямоугольная система координат, мы можем применить метод координат. Разберем его подробнее.

Допустим, в трехмерном пространстве зафиксирована некоторая прямоугольная система координат O x y z , в которой заданы прямая a и плоскость ϒ 1 , параллельные между собой. Требуется определить расстояние между заданными прямой и плоскостью.

Построим решение этой задачи на указанном выше определении расстояния между прямой и параллельной ей плоскостью.

Используем некоторую точку М 1 , принадлежащую прямой a : расстояние от этой точки до заданной плоскости и будет являться искомым расстоянием между параллельными прямой и плоскостью. Определим координаты точки М 1 как ( x 1 , y 1 , z 1 ) и запишем нормальное уравнение плоскости ϒ 1 : cos α · x + cos β · y + cos γ · z — p = 0 . Теперь мы можем вычислить искомое расстояние, для чего применим формулу:

M 1 H 1 = cos α · x 1 + cos β · y 1 + cos γ · z 1 — p

Вывод этой формулы можно изучить в статье о нахождении расстояния от точки до плоскости.

Таким образом, мы можем сформулировать алгоритм для нахождения расстояния между прямой и параллельной ей плоскостью:

— определяем координаты точки, принадлежащей заданной прямой (для этого пригодятся навыки работы с основными видами уравнений в пространстве);

— записываем нормальное уравнение заданной плоскости вида cos α · x + cos β · y + cos γ · z — p = 0 (чтобы легко справиться с этим пунктом, следует повторить материал по основным видам уравнений плоскости и вспомнить навык приведения уравнения плоскости к нормальному виду);

— вычисляем искомое расстояние по формуле: M 1 H 1 = cos α · x 1 + cos β · y 1 + cos γ · z 1 — p

Задана прямая x — 1 2 = y 0 = z + 1 1 и параллельная ей плоскость 3 x + 2 y — 6 z — 2 = 0 . Необходимо определить расстояние между ними.

Решение

Заданные условием задачи канонические уравнения прямой x — 1 2 = y 0 = z + 1 1 дают возможность определить точку М 1 ( 1 , 0 , — 1 ) , принадлежащую этой прямой.

Запишем нормальное уравнение исходной плоскости, т.е. преобразуем заданное условием задачи общее уравнение в нормальный вид. Вычислим нормирующий множитель: 1 3 2 + 2 2 + ( — 6 ) 2 = 1 7 и умножим на него обе части исходного общего уравнения плоскости:

3 x + 2 y — 6 z — 2 = 0 ⇔ 1 7 · 3 x + 2 y — 6 z — 2 = 1 7 · 0 ⇔ 3 7 x + 2 7 y — 6 7 z — 2 7

Теперь можем вычислить требуемое расстояние как расстояние от точки М 1 до плоскости 3 7 x + 2 7 y — 6 7 z — 2 7 = 0 :

M 1 H 1 = 3 7 · 1 + 2 7 · 0 — 6 7 · — 1 — 2 7 = 1

Ответ: 1 .

Заданы прямая 2 x — y + 9 = 0 2 x + y — 2 z + 3 = 0 и параллельная ей плоскость x — 3 2 + y 3 2 + z — 3 = 1 . Необходимо найти расстояние между ними.

Решение

Условием задачи прямая описывается уравнениями двух пересекающихся плоскостей. Определим координаты ( x 1 , y 1 , z 1 ) некой точки М 1 , принадлежащей этой прямой. Искомые координаты должны отвечать условиям уравнений прямой, т.е. координаты ( x 1 , y 1 , z 1 ) будут частным решением системы линейных уравнений 2 x — y + 9 = 0 2 x + y — 2 z + 3 = 0 . Найдем частное решение этой системы.

Примем z = 0 , тогда получим: 2 x — y = — 9 2 x + y = — 3 , откуда x = — 3 , y = 3 .

Таким образом, координаты точки М 1 равны ( — 3 , 3 , 0 ) .

Теперь запишем нормальное уравнение плоскости, заданной условием задачи уравнением плоскости в отрезках. Сначала осуществим переход к общему уравнению плоскости:

x — 3 2 + y 3 2 + z — 2 = 1 ⇔ — 2 3 x + 2 3 y — 1 3 z — 1 = 0

Полученное общее уравнение уже является нормальным уравнением плоскости, поэтому в дальнейших преобразованиях необходимости нет.

Наконец, вычислим расстояние от точки до плоскости, которое и будет являться требуемым расстоянием от заданной прямой к заданной плоскости:

M 1 H 1 = — 2 3 · — 3 + 2 3 · 3 — 1 3 · 0 — 1 = 0 = 3

🎦 Видео

Видеоурок "Расстояние между прямыми в пространстве"Скачать

Записать уравнение прямой параллельной или перпендикулярной данной.Скачать

Определение кратчайшей расстоянии от точки до плоскостиСкачать

Точка встречи прямой с плоскостьюСкачать

Расстояние от точки до плоскости / Вывод формулыСкачать

Геометрия 10 класс (Урок№10 - Перпендикуляр и наклонные.)Скачать

18. Расстояние от точки до прямой в пространствеСкачать

Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

Расстояние между скрещивающимися прямымиСкачать