Найти площадь полной поверхности цилиндра если длина окружности

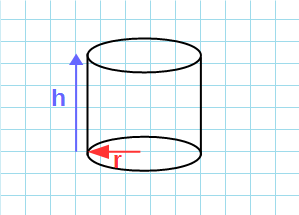
На данной странице калькулятор поможет рассчитать площадь поверхности цилиндра онлайн. Для расчета задайте высоту и радиус.

Цилиндр — геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её.

Боковая поверхность

Формула площадь боковой поверхности цилиндра через высоту и радиус:

Полная поверхность

Формула площадь полной поверхности цилиндра через высоту и радиус:

Онлайн калькулятор площади цилиндра. Как узнать площадь цилиндра.

Вычислить площадь цилиндра через:Вычислить:Длина радиуса R:Длина диаметра D:Высота цилиндра h:

Для того что бы вычислить площадь цилиндра необходимо знать его высоту и радиус или диаметр. Если нам известны указанные величины, для нас не составит труда вычислить площадь.
Полная площадь цилиндра рассчитывается по следующим формулам:

Если нам известен радиус:

Площадь боковой поверхности цилиндра рассчитывается по следующим формулам:

Если нам известен радиус:

Где S – площадь, R – радиус, D – диаметр, h — высота, π – число Пи которое всегда примерно равно 3,14.

Найти площадь полной поверхности цилиндра если длина окружности

Нахождение площади поверхности цилиндра: формула и задачи

В данной публикации мы рассмотрим, как можно найти площадь поверхности цилиндра и разберем примеры решения задач для закрепления материала.

Формула вычисления площади цилиндра

1. Боковая поверхность

Площадь (S) боковой поверхности цилиндра равна произведению длины окружности, являющейся основанием фигуры, на его высоту.

Длина окружности, в свою очередь, рассчитывается так: C = 2 π R. Следовательно, рассчитать площадь можно следующим образом:

Примечание: в вычислениях значение числа π округляется до 3,14.

2. Основание

В качестве оснований цилиндра (равны между собой), выступает круг, площадь которого равна:

Т.к. диаметр круга равен двум его радиусам (d = 2R), выражение можно преобразовать таким образом:

3. Полная площадь

Для нахождения данной величины необходимо просуммировать площади боковой поверхности и двух равных оснований цилиндра, т.е.:

S = 2 π R h + 2 π R 2 или S = 2 π R (h + R)

Примеры задач

Задание 1
Найдите площадь боковой поверхности цилиндра, если его радиус равен 11 см, а высота – 8 см.

Решение:
Воспользуемся первой формулой, подставив в нее данные по условиям задачи значения:
S = 2 ⋅ 3,14 ⋅ 11 см ⋅ 8 см = 552,64 см 2 .

Задание 2
Высота цилиндра равна 9 см, а его диаметр – 8 см. Найдите суммарную площадь поверхности фигуры.

Решение:
Если диаметр цилиндра равен 8 см, значит его радиус составляет 4 см (8 см / 2). Применив соответствующую формулу для нахождения площади получаем:
S = 2 ⋅ 3,14 ⋅ 4 см ⋅ (9 см + 4 см) = 326,56 см 2 .

Площадь поверхности цилиндра

Площадь поверхности цилиндра. В этой статье мы рассмотрим задания связанные с площадью поверхности цилиндра . На блоге уже рассмотрены задания с таким телом вращения как конус. Цилиндр тоже относится к телам вращения. Что требуется и нужно знать о площади поверхности цилиндра? Давайте посмотрим на развёртку цилиндра:

Верхнее и нижнее основание это два равных круга:

Боковая поверхность это прямоугольник. При чём одна сторона этого прямоугольника равна высоте цилиндра, а другая длине окружности основания. Напомню, что длина окружности равна:

Итак, формула поверхности цилиндра:

*Учить эту формулу не нужно! Достаточно знать формулы площади круга и длины его окружности, тогда вы всегда сможете записать указанную формулу. Важно её понимание! Рассмотрим задачи:

Длина окружности основания цилиндра равна 3. Площадь боковой поверхности равна 6. Найдите высоту и площадь поверхности цилиндра (считайте, что число Пи равно 3,14 и результат округлите до десятых).

Площадь полной поверхности цилиндра:

Даны длина окружности основания и площадь боковой поверхности цилиндра. То есть, нам дана площадь прямоугольника и одна его сторона, требуется найти другую сторону (это есть высота цилиндра):

Требуется радиус и тогда мы сможем найти указанную площадь.

Длина окружности основания равна трём, тогда запишем:

Округляем до десятых, получаем 7,4.

Площадь боковой поверхности цилиндра равна 72Пи, а диаметр основания — 9. Найдите высоту цилиндра.

Площадь боковой поверхности цилиндра находится по формуле:

Площадь боковой поверхности цилиндра равна 64Пи, а высота — 8 . Найдите диаметр основания.

Площадь боковой поверхности цилиндра находится по формуле:

Найдём радиус основания и далее определим диаметр:

Диаметр равен двум радиусам, значит:

27058. Радиус основания цилиндра равен 2, высота равна 3. Найдите площадь боковой поверхности цилиндра, деленную на Пи.

27133. Длина окружности основания цилиндра равна 3, высота равна 2. Найдите площадь боковой поверхности цилиндра.

27173. Площадь осевого сечения цилиндра равна 4. Найдите площадь боковой поверхности цилиндра, деленную на Пи.

284361. Площадь боковой поверхности цилиндра равна 2Пи, а диаметр основания — 1. Найдите высоту цилиндра.

284362. Площадь боковой поверхности цилиндра равна 2Пи, а высота — 1. Найдите диаметр основания.

Будет ещё пару статей с цилиндрами, не пропустите!

Онлайн калькулятор. Площадь цилиндра.

Используя этот онлайн калькулятор, вы сможете найти площадь боковой поверхности цилиндра, а также площадь полной поверхности цилиндра.

Воспользовавшись онлайн калькулятором для вычисления площади поверхности цилиндра, вы получите детальное пошаговое решение вашего примера, которое позволит понять алгоритм решения таких задач и закрепить пройденный материал.

Найти площадь поверхности цилиндра

Введите значение радиуса цилиндра и его высоты

R =

h =

Ввод данных в калькулятор для вычисления площади цилиндра

В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.

N.B. В онлайн калькуляте можно использовать величины в однаквых единицах измерения!

Если у вас возниели трудности с преобразованием едениц измерения воспользуйтесь конвертером единиц расстояния и длины и конвертером единиц площади.

Дополнительные возможности калькулятора вычисления площади цилиндра

Теория. Площадь поверхности цилиндра

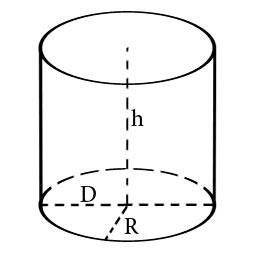
— геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями (основаниями), пересекающими её.

Цилиндр называется круговым, если его основание – круг. Расстояние между основаниями – высота цилиндра.

Формулы для вычисления площади боковой поверхности цилиндра

Формулы для вычисления площади полной поверхности цилиндра

S = 2 π R h + 2 π R 2 = 2 π R ( R + h )

где S — площадь,
R — радиус цилиндра,
h — высота цилиндра,
π = 3.141592.

Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.

Площадь поверхности цилиндра

Всего получено оценок: 9327.

Всего получено оценок: 9327.

Цилиндр представляет собой геометрическое тело, ограниченное двумя параллельными плоскостями и цилиндрической поверхностью. В статье поговорим о том, как найти площадь поверхности цилиндра и, применив формулу, решим для примера несколько задач.

У цилиндра есть три поверхности: вершина, основание, и боковая поверхность.

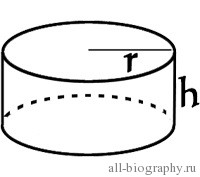
Основаниями цилиндра (их два: верхние и нижнее) являются окружности, их легко определить.

Известно, что площадь окружности равна πr 2 . Поэтому, формула площади двух окружностей (двух оснований цилиндра) будет иметь вид πr 2 + πr 2 = 2πr 2 .

Боковая поверхность цилиндра

Третья, боковая поверхность цилиндра, является изогнутой стенкой цилиндра. Для того чтобы лучше представить эту поверхность попробуем преобразовать её, чтобы получить узнаваемую форму. Представьте себе, что цилиндр, это обычная консервная банка, у которой нет верхней крышки и дна. Сделаем вертикальный надрез на боковой стенке от вершины до основания банки (Шаг 1 на рисунке) и попробуем максимально раскрыть (выпрямить) полученную фигуру (Шаг 2).

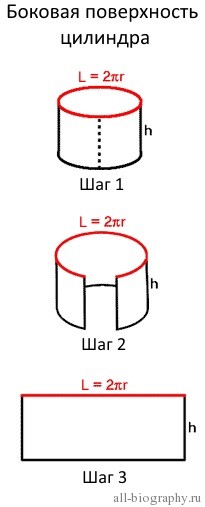
После полного раскрытия полученной банки мы увидим уже знакомую фигуру (Шаг 3), это прямоугольник. Площадь прямоугольника вычислить легко. Но перед этим вернемся на мгновение к первоначальному цилиндру. Верхнее основание исходного цилиндра является окружностью, а мы знаем, что длина окружности вычисляется по формуле: L = 2πr. На рисунке она отмечена красным цветом.

Когда боковая стенка цилиндра полностью раскрыта, мы видим, что длина окружности становится длиной полученного прямоугольника. Сторонами этого прямоугольника будут длина окружности(L = 2πr) и высота цилиндра(h). Площадь прямоугольника равна произведению его сторон – S = длина х ширина = L x h = 2πr x h = 2πrh. В результате мы получили формулу для расчета площади боковой поверхности цилиндра.

Площадь полной поверхности цилиндра

Наконец, если мы сложим площадь всех трёх поверхностей, мы получим формулу площади полной поверхности цилиндра. Площадь полной поверхности цилиндра равна площадь верхнего основания цилиндра + площадь нижнего основания цилиндра + площадь боковой поверхности цилиндра или S = πr 2 + πr 2 + 2πrh = 2πr 2 + 2πrh. Иногда это выражение записывается идентичной формулой 2πr (r + h).

Примеры расчета площади поверхности цилиндра

Для понимания приведенных формул, попробуем посчитать площадь поверхности цилиндра на примерах.

1. Радиус ос­но­ва­ния цилиндра равен 2, высота равна 3. Определите площадь боковой поверхности цилиндра.

Площадь боковой поверхности цилиндра равна 37,68.

2. Как найти площадь поверхности цилиндра, если высота равна 4, а радиус 6?

S = 2 * 3,14 * 6 2 + 2 * 3,14 * 6 * 4

S = 2 * 3,14 * 36 + 2 * 3,14 * 24

Площадь поверхности цилиндра равна 376,8.

3. Площадь боковой поверхности прямого кругового цилиндра равна 24π, а диаметр основания — 3. Найдите высоту цилиндра.

Из формулы расчета площади боковой поверхности цилиндра Sбок. = 2πrh следует, что высота равна:

Значение радиуса получаем из формулы: d = 2r

Найти площадь полной поверхности цилиндра если длина окружности

Шар вписан в цилиндр. Площадь поверхности шара равна 111. Найдите площадь полной поверхности цилиндра.

Высота цилиндра равна диаметру шара, а радиус основания цилиндра равен радиусу шара (см. рис.).

Площадь основания цилиндра:

Площадь боковой поверхности цилиндра:

Площадь полной поверхности цилиндра:

Поскольку площадь поверхности шара дается формулой имеем:

Цилиндр и конус имеют общие основание и высоту. Высота цилиндра равна радиусу основания. Площадь боковой поверхности цилиндра равна Найдите площадь боковой поверхности конуса.

Заметим, что конус и цилиндр имеют общую высоту и равные радиусы основания. Площадь боковой поверхности цилиндра равна откуда, учитывая, что получаем: или

Образующая конуса его высота и радиус основания связаны соотношением откуда, учитывая, что получаем: или

Площадь боковой поверхности конуса равна следовательно:

Цилиндр и конус имеют общее основание, вершина конуса является центром другого основания цилиндра. Каждая образующая конуса наклонена к плоскости основания под углом 30°.

а) Докажите, что площади боковых поверхностей цилиндра и конуса равны

б) Найдите радиус сферы, касающейся боковых поверхностей цилиндра и конуса, а так

же одного из оснований цилиндра, если известно, что объем конуса равен

а) Пусть радиус основания цилиндра равен а высота Тогда тангенс угла наклона образующей есть откуда и образующая конуса равна Вычислим теперь площади боковой поверхности цилиндра и конуса. Это и что и требовалось доказать.

б) Рассмотрим сечение цилиндра и конуса осевой плоскость, проходящей через центр сферы. Все точки касания будут лежать в этой плоскости. В сечении получим окружность, вписанную в прямоугольный треугольник со сторонами поэтому ее радиус равен

C другой стороны, как мы знаем,

откуда поэтому искомый радиус равен 1.

📹 Видео