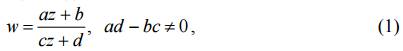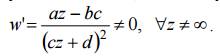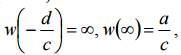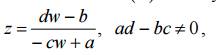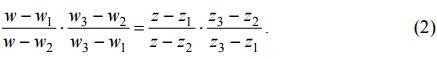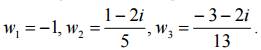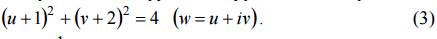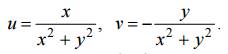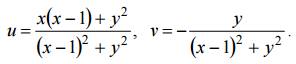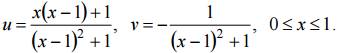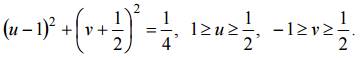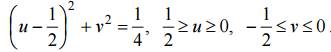Найти образ окружности при дробно линейном отображении (2 видео)

Дробно-линейные отображения

Дробно-линейной функцией называется функция вида: , где — произвольные комплексные числа, такие, что .

Перечислим без доказательства свойства дробно-линейной функции.

Дробно-линейная функция осуществляет взаимно однозначное отображение расширенной комплексной плоскости на себя. При этом точка отображается в точку , а точка отображается в .
Дробно-линейное отображение можно представить в виде суперпозиции трех простейших отображений: целого линейного , отображения и сдвига .
Дробно-линейное отображение отображает окружности и прямые в окружности и прямые. При этом прямая может перейти как в прямую, так и в окружность. Окружность тоже может перейти как в прямую, так и в окружность. Это свойство называется круговым свойством дробно-линейных отображений.
Точки симметричные относительно прямой или окружности переходят в точки симметричные относительно образа этой прямой или окружности.
Дробно-линейное отображение, переводящее три заданные точки в три заданные точки: дается формулой:

Пример 1 Найти образ мнимой оси при отображении .

Мнимая ось представляет собой прямую. По третьему свойству она должна перейти в окружность или в прямую. Найдем образы трех точек мнимой оси: . Так как образ одной из точек , то мнимая ось переходит в прямую проходящую через и , то есть в действительную ось.

Пример 2 Найти дробно линейное отображение, переводящее точки .

Пример 3 Найти образ области при отображении

Найдем образ мнимой оси при данном отображении. Возьмем три точки : .

Отметим также, что . Куда же перешел луч ? Подставим в формулу отображения: . При , точки переходят в точки луча действительной оси. Точки переходят в луч . Образы двух точек действительной оси у нас есть: Действительная ось переходит в окружность, проходящую через точки .

Найдем образ точки из границы нашей области:

Итак, образ луча будет полуокружность .

Теперь мы можем изобразить схему самого отображения:

Пример 4 Найти образы всех квадрантов при отображении .

Чтобы не решать опять задачи подобные примеру 3, воспользуемся следствием принципа симметрии Римана-Шварца в такой формулировке:

Пусть функция отображает область в и — дуга окружности или отрезок, принадлежащий границе области , и — область, симметричная относительно .

Пусть непрерывна на и области и не пересекаются. Тогда функция конформно отображает на , где и — образы и соответственно при отображении .

На следующем рисунке видно, что области и симметричны относительно луча , который переходит в полуокружность . Так находится образ области . Он для удобства обозначен штриховкой. Точно так же находятся образы остальных двух квадрантов.

Длины волн инфракрасного света достаточно велики, чтобы перемещаться сквозь облака, которые в противном случае блокировали бы наш обзор. Используя большие инфракра сные телескопы, астрономы смогли заглянуть в ядро нашей галактики. Большое количество звезд излучают часть своей электромагнитной энергии в виде видимого света, крошечной части спектра, к которой чувствительны наши глаза.

Так как длина волны коррелирует с энергией, цвет звезды говорит нам, насколько она горячая. Используя телескопы, чувствительные к различным диапазонам длин волн спектра, астрономы получают представление о широком круге объектов и явлений во вселенной.

Пример №1 Постройте центральную симметрию тетраэдра, относительно точки O, изображенных на рисунке 3.

Для построения такой центральной симметрии сначала проведем через все точки тетраэдра прямые, каждая из которых будет проходить через точку O. На них построим отрезки, удовлетворяющие условиям |AO|=|A?O|, |BO|=|B?O|, |CO|=|C?O|, |DO|=|D?O| Таким образом, и получим искомую симметрию (рис. 4).

В ряду разных механических движений особенным значением обладают колебания. Это движения и процессы, имеющие периодичность во времени.

В среде электромагнитных явлений также значительное место заняли электромагнитные колебания. В этих колебаниях заряды, токи, электрические и магнитные поля изменяются согласно периодическим законам.

Совет №1 Велосипедист, имеющий скорость 300 м/с, или идеальный газ, оказывающий давление 100 паскалей в большой тепловой машине — это странно.

Нужна помощь с курсовой или дипломной работой?

Содержание

Конформные отображения. Дробно-линейная функция
Конформные отображения. Дробно-линейная функция
Конформные отображения
Преобразования
Преобразования плоскости
Пример с решением:
Пример с решением:
🎦 Видео

Видео:Конформные отображения с помощью линейной функцииСкачать

Конформные отображения. Дробно-линейная функция

Видео:Конформные отображения c помощью дробно-линейной функции: круговое свойствоСкачать

Конформные отображения. Дробно-линейная функция

Определение 1. Функция вида

где a, b, c, d – комплексные числа, называется дробно-линейной.

Отображение, задаваемое этой функцией, называется дробно- линейным.

Условие ad − bc ≠ 0 означает, что w ≠ const . Функция (1) осуществляет конформное отображение расширенной комплексной плоскости Z на расширенную комплексную плоскость w, так как производная

Для 0 c ≠ предполагаем, что

для c = 0 функция (1) становится линейной, т. е. w = az + b и w(∞) = ∞. Функция

является обратной к функции (1). Она также является дробно-линейной и однозначной на расширенной комплексной плоскости, т. е. здесь функция (1) является однолистной.

Каждое дробно-линейное отображение может быть получено в результате последовательного выполнения трех отображений: линейного, отображения w = 1/z и снова линейного отображения.

Дробно-линейные отображения переводят:

1) окружность или прямую в окружность или прямую (круговое свойство);

2) пару точек, симметричных относительно окружности, – в пару то- чек, симметричных относительно образа этой окружности (свойство сохранения симметрии). Здесь «окружность», в частности, может быть прямой, если под последней понимать окружность бесконечного радиуса.

Существует единственное дробно-линейное отображение, которое три разных точки z₁, z₂, z₃ переводит соответственно в три разные точки w₁, w₂, w₃. Это отображение задается формулой

Если одна из точек z_k или w_k (k =1, 2, 3) является бесконечно удаленной точкой, то в формуле (2) разности, в которые входит z_k или w_k, требуется заменить единицами.

Существует бесконечно много дробно-линейных отображений, которые заданную окружность γ отображают на заданную окружность Г, причем область D, для которой γ является границей, отображается на одну из областей, для которой Г является границей.

Для обеспечения единственности дробно-линейного отображения достаточно выполнение одного из условий:

1) заданная точка z₀ ∈ D отображается в заданную точку w₀ ∈ D’, а любая кривая, выходящая из точки z₀, поворачивается на заданный угол α w₀ = f (z₀), α = arg(f ‘(z₀));

2) точки z₀ ∈ D и z₁ ∈ γ отображаются соответственно в заданные точки w₀ ∈ D’ и w₁ ∈ Γ.

Пример 1. Найти образ окружности, заданной уравнением

x 2 + y 2 + 2x − 4y + 1 = 0,

при отображении w = 1/z.

Решение. На основании кругового свойства дробно-линейного отображения окружность переходит в окружность. Для ее нахождения на заданной окружности x 2 + y 2 + 2x − 4y + 1 = 0, выберем три точки, например: z₁ = −1 z₂ = 1 + 2i, z₃ = −3 + 2i, образами которых при отображении w = 1/z будут точки

Точками w₁, w₂, w₃ однозначно определяется образ данной окружности, уравнение которой:

Для отображения w = 1/z имеем

Выразив отсюда x = x(u, v), y = (u, v) и подставив в уравнение заданной окружности, получим искомый образ (3).

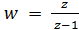
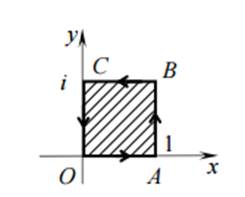
Пример 2. Найти образ области D при отображении , где D = <z, 0

Будем искать образ границы области D (рис. 1).

Сторона OA: y = 0, 0 ≤ x ≤ 1 отображается на отрицательную часть действительной оси (v = 0, − ∞

Рис. 1. Область D

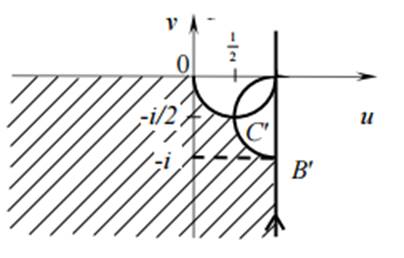
Рис. 2. Образ области D

Сторона AB: x = 1, 0

Сторона BC: y =1, 1 ≥ x ≥ 0, отображается в линию, параметрическое уравнение которой имеет вид

Исключив параметр x, получим

Аналогично образ стороны CO определяется уравнением

В соответствии с принципом соответствия границ образом квадрата будет заштрихованная область на рис. 1.

Пример 3. Найти дробно-линейное отображение, которое точки z₁ = 1 и z₂ = −1 оставляет неподвижными, а точку z₃ = i переводит в точку w₃ = 0.

Найти образ полуплоскости Im(z) > 0 при данном отображении.

Решение. По условию имеем три пары соответствующих точек

Применяя формулу (2), получим искомое дробно-линейное отображение .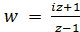

Найдем теперь образ верхней полуплоскости, границей которой является действительная ось. Согласно круговому свойству действительная ось отображается в окружность. Чтобы найти ее, на действительной оси выберем три точки, например: z₁ =1, z₂ = 0, z₃ = −1, образами которых бу- дут точки w₁ = 1, w₂ = −i, w₃ = −1. Они лежат на окружности |w| =1. По принципу соответствия границ получаем, что образом верхней полуплоскости будет область D’= <w, |w|

Пример 4. Найти дробно-линейное отображение, которое круг |z − 4i| u так, что w(4i) = −4, w(2i) = 0.

Решение. Условие задачи определяет две пары соответствующих точек. Третью пару найдем, пользуясь свойством симметрии дробно линейного отображения, согласно которому точки z₁ = 4i и z₃ = ∞, симметричные относительно окружности |z − 4i| = 2, перейдут в точки w₁ = −4 и w₃ = − 4i, симметричные относительно прямой u = v . Таким образом, найдена третья пара точек z₃ = ∞ и w₃ = −4i. По формуле (2) найдем искомое отображение .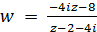

Видео:Дробно Линейное Преобразование | Конформные отображенияСкачать

Конформные отображения

Содержание:

По этой ссылке вы найдёте полный курс лекций по математике:

Преобразования

Преобразования, наделенные таким свойством, позволяют успешно решать задачи аэро- и гидродинамики, теории упругости, теории полей различной природы и многие другие. Мы ограничимся преобразованиями плоских областей. Непрерывное отображение го = /(г) плоской области в область на плоскости называется конформным в точке , если в этой точке оно обладает свойствами постоянства растяжения и сохранения углов.

Открытые области и называются конформно эквивапентными,если существует взаимнооднозначное отображение одной из этих областей на другую, конформное в каждой точке. Теорема Римана. Любые две плоские открытые односвязные области, границы которых состоят более чем из одной точки, конформно эквивалентны. Основной проблемой при решении конкретных задач является построение по заданным плоским областям явного взаимно однозначного конформного отображения одной из них на другую.

Один изспособоврешенияэтой проблемы в плоском случае — привлечение аппарата теории функций комплексного переменного. Какужеотмечалось выше, однолистная аналитическаяфункция с отличной от нуля производной осуществляет конформное отображение своей области задания на ее образ. При построении конформных отображений весьма полезно следующее правило. Принцип соответствия границ.

Пусть в односвязной области Я) комплексной плоскости z, ограниченной контуром 7, задана однозначная аналитическая функция w = f(z), непрерывная в замыкании 9) и отражающая контур 7 на некоторый контур 7′ комплексной п/юскости w. Если при этом сохраняется направления обхода контура, то функция w — f(z) осуществляет конформное отображение области комплексной плоскости z на область З1 комплексной плоскости w, ограниченную контуром 7′ (рис. 1).

Возможно вам будут полезны данные страницы:

Цель настоящего параграфа состоит в том, чтобы, используя найденные ранее области однолистности основных элементарных фуннций комплексного переменного, научиться строить конформные отображения открытых одно-связных плосжх областей, часто встречающихся в приложениях, надвестан- КОНФОРМНЫЕ ОТОБРАЖЕНИЯ дартныс области — верхнюю полуплоскость и единичный круг (рис. 2). Для более эффективного использо- Рис.2 вания приводимой ниже таблицы полезны некоторые простейшие преобразования комплексной плоскости.

Преобразования плоскости

Преобразования плоскости, осуществляющие: 1. параллельный перенос (сдвиг на заданное комплексное число а) (рис. 3), Рис.3 2. поворот (на заданный угол 3. растяжение (fc > 1) ил и сжатие (рис. 5). Тем самым, преобразование вида 0 любой круг можно сделать единичным кругом с центром в нуле (рис. 6), любую полуплоскость можосделать верхней полуплоскостью, любой отрезок прямой можно преобразовать в отрезок [0, 1) вещественной оси (рис. 7), любой луч — в положительный луч вещественной оси (рис. 8). б) Рис. 6 растяжение (им) О перенос в) поворот перенос рас гяжение Рис. 7 перенос поворот Рис.8 в) б) В) 4.

Преобразование плоскости z,

переводящее три различные точки z, zi, z3 в три различныеточт плоскости (рис.9). Рассмотрим пример, показывающий, как пользоваться приведенной ниже табли- цей.

Пример с решением:

Отобразить круг с разрезом по радиусу (рис. 10) взаимно однозначно и конформно на единичный круг с центром в нуле. 4 А. Применяя простейшие преобразования плоскости, приведем заданную область к области, имеющейся в таблице. 1. Переместим центр заданного круга в нулевую точку (см. рис. 11): .

Имеем: круг с разрезом 2. Повернем полученный круг по часовой стрелке на угол (см. рис. 12) . Имеем: круг с разрезом arg 3. Сожмем круг в три раза (см. рис. 13) Имеем: круг с разрезом Таким образом, исходная область приводится к имеющейся в таблице при помощи следующего преобразования Б. 1. Указанная область — круг с разрезом — приведена в таблице под № 30. Функция Жуковского КОНФОРМНЫЕ ОТОБРАЖЕНИЯ преобразует эту область в плоскость с разрезом по отрезку [-1, 5] вещественной оси (рис. 14). 2. Указанная область приведена в таблице под № 22.

Применяя дробно-линейное преобразование преобразуем эту область в плоасость с разрезом по лучу [0, +оо) вещественной оси (рис. 15).

3. Указанная область приведена в таблице под № 6. Извлекая квадратный корень преобразуем эту область в верхнюю полуплоскость Im z6 > 0 (рис. 16). 4. Указанная область приведона в таблице под Ng 11. Применяя дробно- линейное преобразование преобразуем эту область в единичный круге центром в нуле Последовательно выражая z* через z^-i, получим взаимно однозначное и конформное преобразование заданного на комплексной плоскости г круга с разрезом по радиусу на единичный круг комплексной плоек ости tr. р- Конформное отображение заданными областями определяется неоднозначно.

Пример с решением:

Отобразить полукруг (рис.18) взаимно однозначно и конформно на верхнюю полуплоскость Im w > 0. . Дробно-линейное отображение преобразует заданный полукруг в прямой угол 2. Указанная область приведена в таблице под Ne 4 (п = 2). Возводя в квадрат Б. Заданная область приведена в таблице за No 9. Искомое преобразование имеет вид чю- Оба отображения w -заданный полукруг в верхнюю полуплоскость переводит взаимно однозначно и конформно Организация таблицы и правила пользования ею.

Как будет показано в конце параграфа, такая стандартизация удобна для практического использования. Часто приводится только преобразование, сводящее заданную область к ранее рассмотренной. В этом случае дается ссылка на преобразование, переводящее полученную область в стандартную (единичный круг с центром в нуле или верхнюю полуплоскость). Основные элементарные функции.

Таблица Плоскость с разрезом по действительному лучу [О, Плоскость с разрезами Плоскость с разрезом по действительному лучу [0, +ю[ Плоскость с разрезом по отрезку 10, 1] Плоскость с разрезом по действительному лучу (0, +«>( Плоскость с разрезами по действительным лучам J -оо, 0] и (I, +оо[ Плоскость с разрезом по действительному лучу [0, +«>( Плоскость с разрезом по отрезку lu. zi] Плоскость с разрезом по отрезку (О, 1J № 21 1лоскость с разрезами ю лучам, лежащим ia прямой, проходящей через ачало координат по действительным лучам ]-«ю, 0] и (1.

Плоскость с разрезом по действительному лучу (0, +во( Плоскость с разрезом по дуге окружности Ixl — 1, lm z > О Плоскость с разрезом по дуге окруж ности III — I, Re z > О Плоскость с разрезом по действительн ому лучу (0, Плоскость с разрезом no дуге окруж ности Плоскость с разрезом по действительному лучу [С, + со [ № 25 Полуплоскость с разрезами Полуплоскость l с разрезом по отрезку [0, />

Плоскость с разрезом по действительному лучу [ — I, Полуплоскость с разрезом по отрезку Полуплоскость Im г > О с разрезами по отрезку [0, oi) и мнимому лучу №28 Полуплоскость с разрезом по ду| е окружности по действительным лучам |- по действительным лучам 1 — оо, -Л2] с разрезом по мнимому лучу Круг с разрезами Круг 1 с разрезом по отрезку (1/2, 1J №30 Плоскость с разрезом по отрезку <-1, 5/4] Круг Izl с разрезами по отрезкам (-1. -1/2] и (1/2, 1] № 31

Плоскость с разрезами по отрезиам I -5/4, 5/4] Круг Ijl симметричными разрезами по мнимой оси Круг lie с симметричными разрезами по действительной оси Внешность круга с разрезами Внешность единичного круга I с разрезом по отрезку [1, 2J №33 Внешность единичного круга с разрезом по отрезкам 1-2, -1] и 11, 2) №34 Плоскость с разрезом по отрезку [ -1, 5/4] Плоскость с разрезом по отрезку I — 5/4, 3/4] w = e’^z Внешность единичного круга Izl > 1 с разрезами по отрезкам, являющимися продолжениями его диаметра Внешность единичного круга Iwl > 1 с разрезами по отрезкам, лежащим на действительной оси Полуируг с разрезами -г2

Nfc 36 Круг Iwl с разрезом по отрезку [ -1/4, 1] Полукруг , с разрезом по отрезку (0, i/2) Полукруг , с разрезом по отрезку [//2, /) Круг с разрезами по отрезкам № 37 Полукруг с разрезами по отрезкам [0. al) и [Ы. /). где N? 38 Круг с разрезами по отрезкам 1-1. — угол с разрезами Угол с разрезом по действительному лучу Ах» г — т/4 с началом в точке 1 + / Полуплоскость Im W > 0 с разрезом по мнимому лучу с началом в точке 12/, +/•©( Nf39 Плоскость с разрезами по действительным лучам Угол с разрезом по действительному лучу Arg z — т/л с началом в точке Полоса с разрезами w — с*

Полуплоскость Im с разрезом по дуге окружности иг » с Полоса 0 т с разрезом по мнимому отрезку ( Полуплоскость Im с разрезом по дуге окружности w — е Полоса 0 разрезом по мнимому отрезку fW/2, TiJ N? Полоса Полуплоскость Im w > О с разрезами по мнимым с разрезами по дуге отрезкам [0, al и [Ы, «1, окружности w « t*, КОНФОРМНЫЕ ОТОБРАЖЕНИЯ М43 Полоса Плоскость с разрезом по действительному лучу (0. +«( №44 Полоса с разрезом Полуплоскость Im по действительному с разрезом по мнимому лучу I отрезку [О, /I

Полоса 0 Полоса с разрезом по действительному лучу I №46 Полоса Полоса 0 с разрезом по действительному лучу R №47 Область 1 Полоса 01 Область с удаленным кругом Re Полоса Полуплоскость Im z > О с удаленным круговым сегментом Угол №50 -Ш Полуплоскость Im с удаленным круговым сегментом Полуплоскость Im w > 0 № 51 Полуполоса Полуплоскость Im w > Полуплоскость Im Полуполоса с удаленными полукругами № 53

Полуполоса Полуполоса N? 54 Угол Полуплоскость Im w > 0 с удаленным сектором единичного круга Ne 55 Угол Im z с удаленным полукругом Полуполоса 0 Внешность параболы Полуплоскость Im w Внутренность параболы Полуплоскость Im № 58 Внешность гиперболы Полуплоскость Im w Внутренность правой ветви гиперболы Полуплоскость Iro W > О Внешность эллипса Внешность круга М > I

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.