Найти наименьшую площадь треугольника

Зависит от того, какой треугольник.

Чтобы найти площадь треугольника, надо сначала определить тип треугольника: прямоугольный, равнобедренный, равносторонний. Если он у вас не такой – отталкивайтесь от других данных: высоты, вписанной или описанной окружности, длин сторон. Привожу все формулы ниже.

Видео:Как найти площадь треугольника? #треугольник #математика #егэ #shorts #подготовкакегэ #огэ #площадьСкачать

Если треугольник прямоугольный

То есть один из его углов равен 90 градусам.

Надо перемножить катеты и поделить на два. Катеты – это две меньшие стороны, в сравнении с гипотенузой. Гипотенуза – это самая длинная сторона, она всегда находится напротив угла в 90 градусов.

Видео:Площадь треугольника. Как найти площадь треугольника?Скачать

Если он равнобедренный

То есть у него равны боковые стороны. В таком случае надо провести высоту к основанию (той стороне, которая не равна «бедрам»), перемножить высоту с основанием и поделить результат на два.

Видео:Как найти площадь треугольника без формулы?Скачать

Если он равносторонний

То есть все три стороны равны. Ваши действия такие:

1. Найдите квадрат стороны – умножьте эту сторону на нее же. Если у вас сторона равна 4, умножьте 4 на 4, будет 16.
2. Умножьте полученное значение на корень из 3. Это примерно 1,732050807568877293527.
3. Поделите все на 4.

Видео:Геометрия Найдите наименьшую высоту треугольника со сторонами 13 см 20 см и 21 смСкачать

Если известна сторона и высота

Площадь любого треугольника равна половине произведения стороны на высоту, которая к этой стороне проведена. Именно к этой, а не к какой-то другой.

Чтобы провести высоту к стороне, надо найти вершину (угол), которая противоположна этой стороне, а потом опустить из нее на сторону прямую линию под углом в 90 градусов. На картинке высота обозначена синим цветом и буквой h, а линия, на которую она опускается, красным цветом и буквой a.

Видео:Найти наименьшую гимпотенузу. Только для взрослых. 16+Скачать

Если известны две стороны и градус угла между ними

Если вы знаете, чему равны две стороны и угол между ними, то надо найти синус этого угла, умножить его на первую сторону, умножить на вторую и еще умножить на ½:

Видео:Площади фигур - треугольника, параллелограмма, трапеции, ромба. Формула Пика и ЕГЭСкачать

Если известны длины трех сторон

1. Найдите периметр. Для этого сложите все три стороны.
2. Найдите полупериметр – разделите периметр на два. Запомните значение.
3. Отнимите от полупериметра длину первой стороны. Запомните.
4. Отнимите от полупериметра длину второй стороны. Тоже запомните.
5. Отнимите от полупериметра длину третьей стороны. И ее запомните.
6. Умножьте полупериметр на каждое из этих чисел (разницу с первой, второй и третьей стороной).
7. Найдите квадратный корень.

Эта формула еще называется формулой Герона. Возьмите на заметку, если вдруг учитель спросит.

Видео:9 класс, 12 урок, Теорема о площади треугольникаСкачать

Если известны три стороны и радиус описанной окружности

Окружность вы можете описать вокруг любого треугольника. Чтобы найти площадь «вписанного» треугольника – того, который «вписался» в окружность, надо перемножить три его стороны и поделить их на четыре радиуса. Смотрите картинку.

Видео:Найдите площадь треугольника на рисунке ★ Два способа решенияСкачать

Если известны три стороны и радиус вписанной окружности

Если вам удалось вписать в треугольник окружность, значит она обязательно касается каждой из его сторон. Следовательно, расстояние от центра окружности до каждой из сторон треугольника – ее радиус.

Чтобы найти площадь, посчитайте сначала полупериметр – сложите все стороны и поделите на два. А потом умножьте его на радиус.

Это были все способы найти площадь треугольника. Спасибо, что дочитали статью до конца. Лайкните, если не трудно.

Видео:Высшая математика. 3 урок. Аналитическая геометрия. Вычисление площади треугольникаСкачать

Найти наименьшую площадь треугольника

треугольник считается описаным вокруг эллипса если что выполнено
эллипс касается трех сторон так?

гм наверно надо пинать тот вариант что не очень хорошо получается

Может с некоторым опозданием, но меня посетила следующая мысль.

Начало, как и говорилось выше, это замена, связанная с растяжением/сжатием по осям. при этом касательные перейдут в касательные, а площадь измениться пропорционально коэффициентам растяжения/сжатия.

И вот дальше возникшая мысль о используемых переменных задачи.
Мы имеем треугольник, в который вписана единичная окружность. Рассмотрим в качестве переменных — углы при основании.

рисунок.

Поскольку центр вписанной окружности лежит на биссектрисах, то мы легко выражаем части сторон треугольника от вершины до основания радиуса через углы. с учётом того, что радиус равен 1.
`AF = AD = ctg(phi), CF = CE = ctg(psi), BD = BE = ctg(pi/2 — phi — psi) = tg(phi + psi)`

Следовательно, `S_ = p*r = ctg(phi) + ctg(psi) + tg(phi + psi)` . и условия на углы `phi >= 0, psi >= 0, phi + psi

Ну, вот . вроде обозримая задача получилась.

Видео:Задача найти площади треугольников при пересечении медианСкачать

Площадь треугольника онлайн

С помощю этого онлайн калькулятора можно найти площадь треугольника. Для нахождения площади треугольника введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть смотрите ниже.

Видео:✓ Новая формула площади треугольника | Ботай со мной #108 | Борис ТрушинСкачать

Площадь треугольника по основанию и высоте

Любой из сторон треугольника можно называть основанием треугольника. Если основание выбрана, то под словом «высота» понимают высоту треугольника, проведенную к основанию (Рис.1):

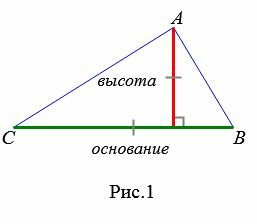Теорема 1. Площадь треугольника равна половине произведения его основания на высоту.

Доказательство. Пусть AC основание треугольника ABC (Рис.2).

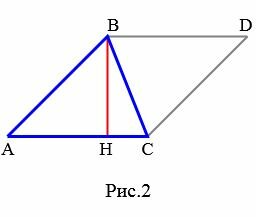Проведем высоту BH. Обозначим через S площадь треугольника. Докажем, что

Из вершины B проведем прямую, параллельную стороне AC, а из C − прямую, параллельную стороне AB. Поскольку ( small AC || BD ) и ( small AB || CD ), то ABDC является параллелограммой и, следовательно, ( small AC = BD ), ( small AB = CD . ) Тогда треугольники ABC и BCD равны по трем сторонам (см. статью на странице Треугольники. Признаки равенства треугольников). Так как площадь параллелограмма ABDC равна ( small S_=AC cdot BH, ) то площадь треугольника ABC (и BCD)равна половине площади параллелограмма:

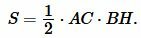Следствие 1. Если высоты треугольников равны, то их площади относятся как основания.

,

,

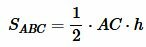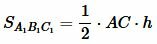Обозначим через k отношение

.

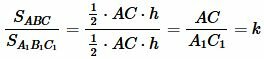То есть отношение площадей треугольников с равными высотами равно отношению их оснований.

Следствие 2. Площадь прямоугольного треугольника равна половине произведения его катетов.

Действительно. Поскольку в прямоугольном треугольнике катеты перпендикулярны друг другу, то один из них можно определить как основание, а другой − как высоту. Тогда по теореме 1, площадь прямоугольного треугольника равна половине произведения его катетов.

Видео:Как найти площадь треугольникаСкачать

Площадь треугольника по двум сторонам и углу между ними

Теорема 2. Площадь треугольника равна половине произведения двух его сторон на синус угла между ними.

Доказательство. Обозначим через S площадь треугольника ABC и пусть a=BC, b=AC (Рис.3). Докажем, что

.

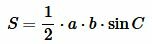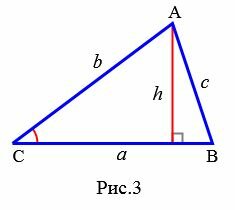Площадь данного треугольника можно вычислить по формуле, полученной выше (теорема 1):

,

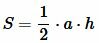(1)

где h − высота треугольника.

,

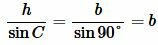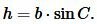(2)

Подставляя (2) в (1), получим:

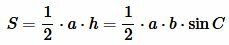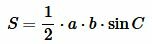(3)

Видео:Задача из КембриджаСкачать

Площадь треугольника по стороне и прилежащим двум углам

Пусть известна сторона треугольника и две прилежащие углы (Рис.4).

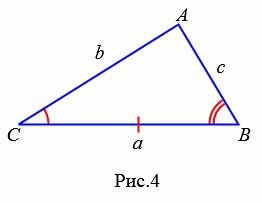Найдем формулу площади этого треугольника. Обозначим через S площадь треугольника. Если у треугольника известны два угла, то можно найти и третий угол:

(4)

Найдем сторону b используя теорему синусов:

,

.

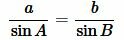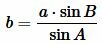(5)

В предыдующем параграфе мы вывели площадь треугольника по двум сторонам и углу между ними. Подставляя (4) и (5) в (3), получим:

.

.

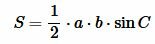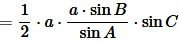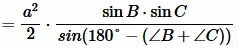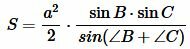(6)

Видео:Площадь прямоугольного треугольника. Как найти площадь прямоугольного треугольника?Скачать

Площадь треугольника по трем сторонам. Формула Герона

Для нахождения площади треугольника по трем сторонам используют формулу Герона:

,

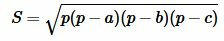(7)

где a, b, c − стороны треугольника, а p − полупериод треугольника:

.

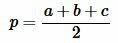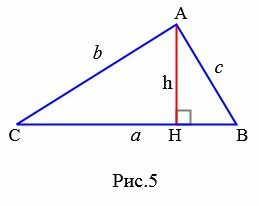Доказательство формулы Герона. На рисунке 5 треугольник ABC имеет стороны a=BC, b=AC, c=AB. Проведем высоту h=AH. Обозначим x=CH. Тогда BH=a−x. Применим теорему Пифагора для треугольников AHC и AHB:

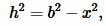(8)

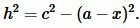(9)

Из (8) и (9) следует:

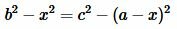Откуда находим x:

,

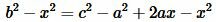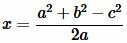(10)

Подставляя (10) в (8) найдем h:

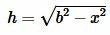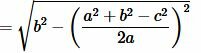(11)

Тогда площадь треугольника равна:

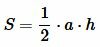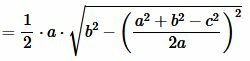(12)

Преобразовав (12) получим формулу (7):

.

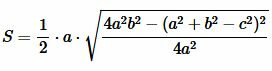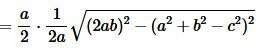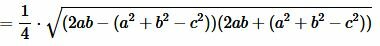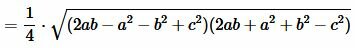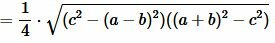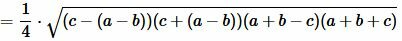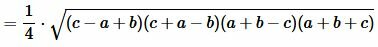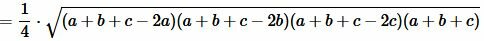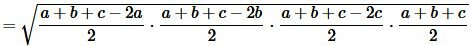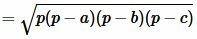Видео:Нахождение площади равнобедренного треугольника при помощи теоремы Пифагора | Геометрия | АлгебраСкачать

Площадь треугольника по трем сторонам и радусу описанной окружности

Пусть известны все три стороны треугольника и радиус описанной окружности (Рис.6). Докажем, что площадь треугольника равна: ( small S=frac. )

📺 Видео

Геометрия 8 класс (Урок№10 - Площадь треугольника.)Скачать

Треугольник наименьшего периметра и наименьшей площади, содержащей две окружностиСкачать

18 ЗАДАНИЕ ОГЭ НАЙТИ ПЛОЩАДЬ ТРЕУГОЛЬНИКАСкачать

Найти площадь треугольника АВС. Задачи по рисункамСкачать

Найдите площадь треугольника АВС, если А(5;2;6), В(1;2;0), С(3;0;3)Скачать