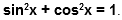Найти координаты точки окружности соответствующей углу 630 градусов

Видео:Алгебра 10 класс Поворот точки вокруг начала координат ЛекцияСкачать

Тригонометрический круг со всеми значениями, круг синусов и косинусов, линия, ось тангенса на окружности, как пользоваться и находить точки

В каждой профессии существуют свои инструменты, обеспечивающие решение и качественное выполнение определенных задач. Математики применяют тригонометрический круг, позволяющий легко и быстро вычислить значение какой-либо функции. Однако не все могут им правильно пользоваться, поскольку не понимают основных понятий.

Видео:Как найти координаты точек на тригонометрической окружностиСкачать

Общие сведения

Для правильного решения тригонометрических задач следует изучить основные понятия, формулы, а также методы нахождения основных величин. Раздел математики, изучающий функции косинуса, синуса, тангенса, котангенса, арксинуса, арккосинуса, арктангенса и арккотангенса, называется тригонометрией. Окружность, которая используется для решения геометрических задач на плоскости, имеет единичный радиус.

Значения функций, которые можно по ней находить, называются тригонометрическими. Однако существует множество способов нахождения их значений, но в некоторых ситуациях при использовании формул приведения решение затянется на продолжительное время, а вычисления будут громоздкими. Чтобы этого избежать, нужно использовать тригонометрический круг со всеми значениями. С его помощью также можно определить, является ли функция четной или нечетной.

Углы и их классификация

Перед тем как понять основное назначение тригонометрических функций, следует обратить внимание на классификацию углов. Она является важной для вычисления тригонометрических выражений. Углы в математических дисциплинах делятся на следующие типы:

К первому типу относятся углы любой размерности градусной единицы измерения, которая не превышает 90 (а Информация о функциях

Тригонометрических функций всего четыре вида: синус (sin), косинус (cos), тангенс (tg) и котангенс (ctg). Существует столько же типов обратных функций: арксинус (arcsin), арккосинус (arccos), арктангенс (arctg) и арккотангенс (arcctg). Они получили широкое применение не только в математических задачах, но также используются в физике, электронике, электротехнике и других дисциплинах. Основной их особенностью считается возможность представления какого-либо закона.

Например, зависимость амплитуды напряжения переменного тока от времени описывается следующим законом: u = Um * cos (w*t) (графиком является косинусоида). Гармонические звуковые колебания также подчиняются определенному закону, в котором присутствует тригонометрическая функция. Кроме того, можно находить значения корня тригонометрического уравнения.

Синусом угла называется величина, равная отношению противолежащего катета прямоугольного треугольника к его гипотенузе. Следовательно, косинус — отношение прилежащего катета к гипотенузе. Тангенс — отношение величины противолежащего катета к прилежащему. Котангенс является обратной функцией тангенсу, т. е. отношение прилежащего к противолежащему.

Функции arcsin, arccos, arctg, arcctg применяются в том случае, когда нужно найти значение угла в градусах или радианах. Вычисления выполняются по специальным таблицам Брадиса или с помощью программ. Также можно использовать тригонометрическую окружность.

Видео:Найти координаты точки единичной окружности полученной при повороте точки Ро(1;0) на угол π, 450°...Скачать

Тригонометрический круг

Чтобы воспользоваться тригонометрической окружностью для решения задач, нужны такие базовые знания: понятие о синусе, косинусе, тангенсе, котангенсе, системе координат и теореме Пифагора. Для построения единичной окружности используется декартовая система координат с двумя осями. Точка «О» — центр пересечения координатных осей, ОХ — ось абсцисс, ОУ — ординат.

Для решения задач различного типа применяется и теорема Пифагора. Она справедлива только для прямоугольного треугольника (один из углов — прямой). Ее формулировка следующая: квадрат гипотенузы в произвольном прямоугольном треугольнике равен сумме квадратов катетов. Следует также знать основные соотношения между функциями острых углов в заданном прямоугольном треугольнике:

Существуют и другие тригонометрические тождества, но для работы с кругом этого перечня будет достаточно.

Построение «инструмента»

Построить окружность, которая ускорит процесс решения задач, довольно просто. Для этого потребуются бумага, карандаш, резинка и циркуль. Далее необходимо нарисовать любую немаленькую окружность. После этого отметить ее центр карандашом, поставив точку. Пусть она будет называться «О». Через эту точку следует провести две перпендикулярные прямые (угол пересечения равен 90 градусам). Обозначить их следующим образом: «х» (горизонтальная) и «у» (вертикальная).

Окружность является единичной, но не стоит рисовать ее такой, поскольку работать будет неудобно. Этот прием называется масштабированием. Он широко применяется практически во всех сферах человеческой деятельности. Например, инженеры не чертят двигатель космического корабля в натуральную величину, поскольку с таким «рисунком» будет неудобно и невозможно работать. Они используют его макет.

Окружность пересекается с осями декартовой системы координат в 4 точках со следующими координатами: (1;0), (0;1), (-1;0) и (0;-1). Области, которые делят декартовую систему координат на 4 части, называются четвертями. Их четыре:

• Первая состоит из положительных координат по х и у.
• Вторая имеет по х отрицательные и положительные по у.
• Третья — только отрицательные значения.
• Четвертая — положительные значения по х и отрицательные по у.

Исходя из этих особенностей, определяется числовой знак функции, позволяющий определить ее четность и нечетность. Кроме того, на ней следует отметить углы следующим образом: 0 и 2ПИ соответствует точке с координатами (1;0), ПИ/2 — (0;1), ПИ — (-1;0) и 3ПИ/2 — (0;-1).

Готовый макет

Для решения задач специалисты рекомендуют иметь рабочий и готовый макеты тригонометрических окружностей. Первый применяется для нахождения значений нестандартных углов (например, синуса 185 градусов). Тригонометрическим кругом (рис. 1) удобно пользоваться в том случае, когда значение угла является стандартным (90, 60 и т. д.).

Рисунок 1. Готовый макет тригонометрического круга синусов и косинусов.

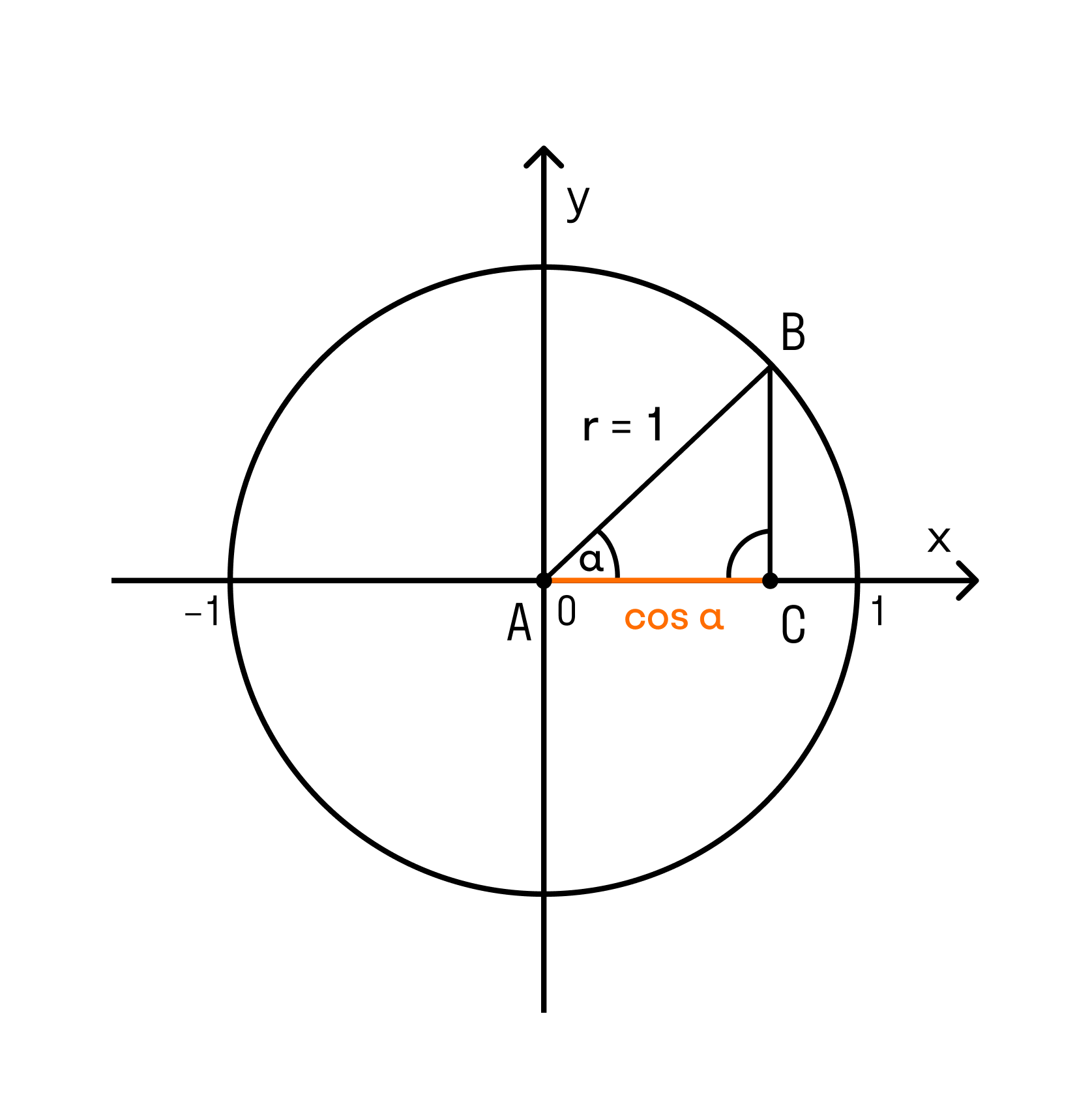
Для нахождения необходимых значений объединяют две фигуры — единичную окружность и прямоугольный треугольник. Гипотенуза последнего равна 1 и соответствует радиусу окружности. Ось ОХ — косинусы, ОУ — синусы. С помощью этого «инструмента» определение синусов и косинусов становится намного проще. Для нахождения значения sin(30) необходимо воспользоваться следующим алгоритмом:

• Отметить угол на окружности и достроить его до прямоугольного треугольника.
• Если катет лежит напротив угла в 30 градусов, то он равен 0,5 от длины гипотенузы.
• sin(30) = 1 * 0,5 = 0,5.

Для нахождения косинуса необходимо использовать основное тригонометрическое тождество, которое связывает sin и cos: (sin(a))^2 + (cos(a))^2 = 1. Из равенства величина cos(30) = sqrt[1 — (sin(30))^2]= sqrt[1 — 0,5^2] = sqrt(3) / 2.

Однако после всех вычислений следует выбрать знак функции. В данном случае угол находится в первой четверти. Следовательно, функция имеет положительный знак. Для нахождения тангенса и котангенса можно воспользоваться следующими формулами: tg(a) = sin(a) / cos(a) и ctg(a) = cos(a) / sin(a). Подставив значения синуса и косинуса, можно определить значение tg: tg(30) = 0,5 / (sqrt(3) / 2) = 1 / sqrt(3) = sqrt(3) / 3. Тогда котангенс можно найти двумя способами:

• Через известный тангенс: ctg(30) = 1 / (1 / sqrt(3)) = sqrt(3).
• Использовать основное отношение: ctg(30) = (sqrt(3) / 2) / (1/2) = sqrt(3).

Вычислить значения синуса и косинуса для угла 60 градусов очень просто. Для этого нужно воспользоваться основными тождествами: sin(60) = сos(30) = sqrt(3) / 2, cos(60) = sin(30) = 1/2, tg(30) = ctg(60) = sqrt(3) / 3, tg(60) = ctg(30) = sqrt(3). Значения для 45 градусов определяются следующим образом:

• Прямоугольный треугольник с углом 45 градусов является равносторонним (катеты равны).
• (sin(45))^2 + (cos(45))^2 = 1.
• 2 * (sin(45))^2 = 1.
• sin(45) + cos(45) = sqrt(2) / 2.

Тангенс и котангенс равен 1. Если угол равен 90, то необходимо внимательно посмотреть на рисунок 1. Следовательно, sin(90) = 1, cos(90) = 0, tg(90) = 1 и ctg(90) не существует. Линия тангенса на окружности не отображается. В этом случае нужно пользоваться основными тригонометрическими тождествами.

Правила использования

Инструмент позволяет легко и быстро находить значения тригонометрических функций любых углов. Если при решении задачи требуется найти sin(270), то нужно выполнить простые действия:

• Пройти против часовой стрелки (положительное направление) 180 градусов, а затем еще 90.
• На оси синусов значение составляет -1 (точка лежит на оси).

Существуют задачи, в которых угол представлен отрицательным значением. Например, нужно определить синус, косинус, тангенс и котангенс угла (-7ПИ/6). В некоторых случаях заданное значение следует перевести в градусы: -7ПИ/6 = -210 (градусам). Если в условии отрицательный угол, то движение следует осуществлять по часовой стрелке от нулевого значения (пройти полкруга, а затем еще 30). Можно сделать вывод о том, что значение -210 соответствует 30. Следовательно, синус вычисляется следующим образом: sin(-210) = -(sin(ПИ + 30)) = — 1/2, cos(-210) = sqrt(3)/2, tg(-210) = sqrt(3)/3 и ctg(-210) = sqrt(3).

Пример случая, когда нет необходимости переводить радианы в градусы, является следующим: нужно вычислить значения тригонометрических функций угла 5ПИ/4. Необходимо расписать значение угла таким образом: 5ПИ/4 = ПИ + ПИ/4. Против часовой стрелки следует пройти половину круга (ПИ), а затем его четвертую часть (ПИ/4). Далее нужно спроецировать координаты точки на ось синусов и косинусов. Это соответствует значению sqrt(2)/2. Тангенс и котангенс заданного угла будут равны 1.

Встречаются задачи, в которых значение угла превышает 360 градусов. Например, требуется найти значения тригонометрических функций угла (-25ПИ/6). Для решения необходимо разложить угол следующим образом: (-25ПИ/6) = — (4ПИ + ПИ/6). Можно не делать обороты, поскольку 4ПИ соответствует двойному обороту и возврату в точку (-ПИ/6). Это объясняется периодом функций синуса и косинуса, который равен 2ПИ. Значения функций sin, сos, tg и ctg равны следующим значениям: — 1/2, sqrt(3)/2, sqrt(3)/3 и sqrt(3) соответственно.

Таким образом, тригонометрический круг позволяет оптимизировать вычисления в дисциплинах с физико-математическим уклоном, в которых используются тригонометрические функции. Не имеет смысла устанавливать дополнительное программное обеспечение, пользоваться таблицами, поскольку это занимает некоторое время. При помощи этого «универсального инструмента» можно найти значение любого угла.

Видео:Как искать точки на тригонометрической окружности.Скачать

Углы 0°,30°,45°,60°,90°,180°,270°,360°,(π/6,π/4,π/3,π/2,π,3π/2,2π). Синусы, косинусы, тангенсы и котангенсы. Таблица значений тригонометрических функций.

Углы 0°,30°,45°,60°,90°,180°,270°,360°,(π/6,π/4,π/3,π/2,π,3π/2,2π). Синусы, косинусы, тангенсы и котангенсы.

Углы 0°,30°,45°,60°,90°,180°270°,360°,(π/6,π/4,π/3,π/2,π,3π/2,2π). Sin, Cos, tg, ctg.

Раздел: Таблицы численных значений + Таблицы Брадиса:

Видео:Алгебра 10 класс. 20 сентября. Числовая окружность #6 координаты точекСкачать

Единичная окружность

О чем эта статья:

10 класс, ЕГЭ/ОГЭ

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Видео:ТРИГОНОМЕТРИЯ С НУЛЯ - Единичная Окружность // Подготовка к ЕГЭ по МатематикеСкачать

Единичная окружность в тригонометрии

Все процессы тригонометрии изучают на единичной окружности. Сейчас узнаем, какую окружность называют единичной и дадим определение.

Единичная окружность — это окружность с центром в начале прямоугольной декартовой системы координат и радиусом, равным единице.

Прямоугольная система координат — прямолинейная система координат с взаимно перпендикулярными осями на плоскости или в пространстве. Наиболее простая и поэтому часто используемая система координат.

Радиус — отрезок, который соединяет центр окружности с любой точкой, лежащей на окружности, а также длина этого отрезка. Радиус составляет половину диаметра.

Единичную окружность с установленным соответствием между действительными числами и точками окружности называют числовой окружностью.

Поясним, как единичная окружность связана с тригонометрией.

В тригонометрии мы постоянно сталкиваемся с углами поворота. А углы поворота связаны с вращением по окружности.

Угол поворота — это угол, который образован положительным направлением оси OX и лучом OA.

Величины углов поворота не зависят от радиуса окружности, по которой происходит вращение, поэтому удобно работать именно с окружностью единичного радиуса. Это позволяет избавиться от коэффициентов при математическом описании. Вот и все объяснение полезности единичной тригонометрической окружности.

Все углы, которые принадлежат одному семейству, дают одинаковые абсолютные значения тригонометрических функций, но эти значения могут различаться по знаку. Вот как:

• Если угол находится в первом квадранте, все тригонометрические функции имеют положительные значения.
• Для угла во втором квадранте все функции, за исключением sin и cos, отрицательны.
• В третьем квадранте значения всех функций, кроме tg и ctg, меньше нуля.
• В четвертом квадранте все функции, за исключением cos и sec, имеют отрицательные значения.

Градусная мера окружности равна 360°. Чтобы решать задачи быстро, важно запомнить, где находятся углы 0°; 90°; 180°; 270°; 360°. Единичная окружность с градусами выглядит так:

Радиан — одна из мер для определения величины угла.

Один радиан — это величина угла между двумя радиусами, проведенными так, что длина дуги между ними равна величине радиуса.

Число радиан для полной окружности — 360 градусов.

Длина окружности равна 2πr, что превышает длину радиуса в 2π раза.

Поскольку по определению 1 радиан — это угол между концами дуги, длина которой равна радиусу, в полной окружности заключен угол, равный 2π радиан.

Потренируемся переводить радианы в градусы. В полной окружности содержится 2π радиан, или 360 градусов. Таким образом:

• 2π радиан = 360°
• 1 радиан = (360/2π) градусов
• 1 радиан = (180/π) градусов
• 360° = 2π радиан
• 1° = (2π/360) радиан
• 1° = (π/180) радиан

Кстати, определение синуса, косинуса, тангенса и котангенса в тригонометрии дается через координаты точек на единичной окружности. Эти определения дают возможность раскрыть свойства синуса, косинуса, тангенса и котангенса.

Уравнение единичной окружности

При помощи этого уравнения, вместе с определениями синуса и косинуса, можно записать основное тригонометрическое тождество:

Курсы по математике в онлайн-школе Skysmart помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.

Видео:10 класс, 11 урок, Числовая окружностьСкачать

Радианная мера угла. Поворот точки вокруг начала координат.
методическая разработка по алгебре (10, 11 класс) на тему

Карточки для проведения самостоятельной работы. Можно использовать на уроках для закрепления темы.

Видео:Радианная мера угла. 9 класс.Скачать

Скачать:

Видео:Решение задач по теме "Поворот точки вокруг начала координат"Скачать

Предварительный просмотр:

Перевести в радианную меру углы:

Перевести в градусную меру углы:

Найти координаты точки окружности, соответствующей углу:

Записать все углы в радианах, соответствующие точке на окружности с координатами:

Записать все углы, на которые нужно повернуть точку P (1; 0) , чтобы получить точку с координатами:

1. :
2. :
3. :

1. :
2. :
3. :

Перевести в радианную меру углы:

Перевести в градусную меру углы:

Найти координаты точки окружности, соответствующей углу:

Записать все углы в радианах, соответствующие точке на окружности с координатами:

Записать все углы, на которые нужно повернуть точку P (1; 0) , чтобы получить точку с координатами:

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

По теме: методические разработки, презентации и конспекты

Урок «Поворот точки вокруг начала координат»

Второй урок темы «Тригонометрические функции» на 1-ом курсе в ОУ НПО. Тип урока: освоение нового материала. Понятия: угол, единичная окружность, координаты точки на окружности, поворот точки вокруг на.

Презентация «Начала тригонометрии. Радианная мера угла»

Презентация предназначена для проведения первого урока по тригонометрии.

Контрольная работа по геометрии 9 класс «Радианная мера угла»

в контрольной работе представлено 4 различных варианта.

«Угол поворота. Радианная мера угла»

Презентация по математике для 10 класчса по теме «Угол поворота, Радианная и градусная мера» .

Презентация к уроку «Радианная мера угла»

Презентация к уроку изучения нового материала в 10 классе по учебнику Ш.А.Алимова. Выполнена в программе SMART Notebook.

Видео:Радианная Мера Угла - Как Переводить Градусы в Радианы // Урок Алгебры 10 классСкачать

10.V-3. Поворот точки вокруг начала координат-2

Алгебра. 10 класс. Тригонометрия. Тест 3.

Вариант 1.

1. Найти координаты точки единичной окружности, полученной поворотом точки (1; 0) на угол 3π/2±π.

A) (0; -1); B) (0; 1); C) (1; 0); D) (-1; 0).

2. Найти координаты точки единичной окружности, полученной поворотом точки (1; 0) на угол π/6±π.

3. Найти координаты точки единичной окружности, полученной поворотом точки (1; 0) на угол π+πk, где kϵZ.

A) (-1; 0); (1; 0); B) (0; -1); (1; 0); C) (1; 0); (0; 1); D) (0; -1); (-1; 0).

4. Записать все углы, на которые нужно повернуть точку Р(1; 0), чтобы в результате получить

A) 3π/4+2πk, kϵZ; B) -π/4+2πk, kϵZ; C) π/4+2πk, kϵZ; D) 7π/4+2πk, kϵZ.

5. Записать все углы, на которые нужно повернуть точку Р(1; 0), чтобы в результате получались

A) π/6+πk, kϵZ; B) π/3+2πk, kϵZ; C) -π/3+πk, kϵZ; D) -π/6+2πk, kϵZ.

6. При повороте точки Р(1; 0) вокруг начала координат получены углы α=π/2+πk, kϵZ. Записать те из них, которые принадлежат отрезку [-5π; -7π/2].

A) -9π/2; -4π; B) -9π/2; -7π/2; C) -7π/2; D) -5π; -9π/2.

7. Точке М единичной окружности соответствует бесконечное множество действительных чисел ±5π/6+2πk, где kϵZ. Записать те из них, которые принадлежат отрезку [3π; 9π/2].

A) 19π/6; B) 17π/6; C) 4π; D) 13π/6.

8. Точке М единичной окружности соответствует бесконечное множество действительных чисел ±π/3+πk, где kϵZ. Записать те из них, которые принадлежат отрезку [-2π; -π/2].

A) -5π/3; -4π/3; B) -4π/3; -2π/3; C) -5π/3; -4π/3; -2π/3; D) -2π; -4π/3; -2π/3.

Вариант 2.

1. Найти координаты точки единичной окружности, полученной поворотом точки (1; 0) на угол π/2±π.

A) (0; -1); B) (0; 1); C) (1; 0); D) (-1; 0).

2. Найти координаты точки единичной окружности, полученной поворотом точки (1; 0) на угол π/3±π.

3. Найти координаты точки единичной окружности, полученной поворотом точки (1; 0) на угол -π+πk, где kϵZ.

A) (-1; 0); (0; -1); B) (0; -1); (1; 0); C) (1; 0); (0; 1); D) (1; 0); (-1; 0).

4. Записать все углы, на которые нужно повернуть точку Р(1; 0), чтобы в результате получить

A) 5π/6+2πk, kϵZ; B) π/6+2πk, kϵZ; C) -π/6+2πk, kϵZ; D) 5π/3+2πk, kϵZ.

5. Записать все углы, на которые нужно повернуть точку Р(1; 0), чтобы в результате получались

A) -π/4+πk, kϵZ; B) π/4+πk, kϵZ; C) -π/8+πk, kϵZ; D) -π/6+2πk, kϵZ.

6. При повороте точки Р(1; 0) вокруг начала координат получены углы α=πk, kϵZ. Записать те из них, которые принадлежат отрезку [4π; 11π/2].

A) 9π/2; 5π; B) 4π; 9π/2; C) 4π; 5π; D) 5π.

7. Точке М единичной окружности соответствует бесконечное множество действительных чисел -π/4+2πk, где kϵZ. Записать те из них, которые принадлежат отрезку [-9π/2; -3π].

A) -13π/4; B) -19π/4; C) -15π/4; D) -17π/4.

8. Точке М единичной окружности соответствует бесконечное множество действительных чисел ±2π/3+2πk, где kϵZ. Записать те из них, которые принадлежат отрезку [-5π; -7π/2].

A) -16π/3; B) -14π/3; C) -13π/3; D) -3π; -14π/3.

Вариант 3.

1. Найти координаты точки единичной окружности, полученной поворотом точки (1; 0) на угол -π/2±π.

A) (0; 1); B) (0; -1); C) (1; 0); D) (-1; 0).

2. Найти координаты точки единичной окружности, полученной поворотом точки (1; 0) на угол 3π/4±π.

3. Найти координаты точки единичной окружности, полученной поворотом точки (1; 0) на угол -3π/2+πk, где kϵZ.

A) (-1; 0); (0; -1); B) (0; 1); (0; -1); C) (1; 0); (0; 1); D) (1; 0); (-1; 0).

4. Записать все углы, на которые нужно повернуть точку Р(1; 0), чтобы в результате получить

A) 5π/3+2πk, kϵZ; B) π/3+2πk, kϵZ; C) π/6+2πk, kϵZ; D) 7π/6+2πk, kϵZ.

5. Записать все углы, на которые нужно повернуть точку Р(1; 0), чтобы в результате получались

A) -π/6+πk, kϵZ; B) -π/4+πk, kϵZ; C) -π/3+πk, kϵZ; D) π/6+2πk, kϵZ.

6. При повороте точки Р(1; 0) вокруг начала координат получены углы α=5π/6+2πk, kϵZ. Записать те из них, которые принадлежат отрезку [-6π; -4π].

A) -5π; B) -29π/6; C) -25π/6; D) -31π/6.

7. Точке М единичной окружности соответствует бесконечное множество действительных чисел ±π/4+2πk, где kϵZ. Записать те из них, которые принадлежат отрезку [-5π; -3π].

A) -17π/4; B) -15π/4; C) -15π/4; -17π/4; D) -13π/4; -15π/4.

8. Точке М единичной окружности соответствует бесконечное множество действительных чисел π/4+πk/2, где kϵZ. Записать те из них, которые принадлежат отрезку [5π; 13π/2].

A) 21π/4; 23π/4; 25π/4; B) 21π/4; 23π/4; C) 23π/4; 25π/4; D) 23π/4.

Вариант 4.

1. Найти координаты точки единичной окружности, полученной поворотом точки (1; 0) на угол -3π/2±π.

A) (-1; 0); B) (0; 1); C) (1; 0); D) (0; -1).

2. Найти координаты точки единичной окружности, полученной поворотом точки (1; 0) на угол 5π/6±π.

3. Найти координаты точки единичной окружности, полученной поворотом точки (1; 0) на угол 3π/2+πk, где kϵZ.

A) (-1; 0); (0; -1); B) (0; -1); (0; 1); C) (1; 0); (0; 1); D) (1; 0); (-1; 0).

4. Записать все углы, на которые нужно повернуть точку Р(1; 0), чтобы в результате получить

A) π/3+2πk, kϵZ; B) -π/3+2πk, kϵZ; C) 2π/3+2πk, kϵZ; D) π/6+2πk, kϵZ.

5. Записать все углы, на которые нужно повернуть точку Р(1; 0), чтобы в результате получались

A) π/6+πk, kϵZ; B) -π/4+πk, kϵZ; C) π/3+πk, kϵZ; D) π/4+πk, kϵZ.

6. При повороте точки Р(1; 0) вокруг начала координат получены углы α=π/3+2πk, kϵZ. Записать те из них, которые принадлежат отрезку [-5π/2; -π].

A) -5π/3; B) -π/3; -4π/3; C) -2π/3; D) -4π/3.

7. Точке М единичной окружности соответствует бесконечное множество действительных чисел ±π/3+2πk, где kϵZ. Записать те из них, которые принадлежат отрезку [-2π; -π/2].

A) -π/3; B) -2π/3; C) -4π/3; D) -5π/3.

8. Точке М единичной окружности соответствует бесконечное множество действительных чисел π/4+πk/2, где kϵZ. Записать те из них, которые принадлежат отрезку [-7π/2; -5π/2].

A) -13π/4; B) -13π/4; -11π/4; C) -11π/4; D) -3π.

🌟 Видео

10 класс, 12 урок, Числовая окружность на координатной плоскостиСкачать

Точки, полученные поворотом точки Р (1; 0) вокруг начала координат на заданные углыСкачать

9 класс. Геометрия. Тригонометрические функции угла от 0° до 180°. Единичная окружность. Урок #1Скачать

Изобразить на единичной окружности точку.Скачать

Координаты точек на числовой окружности, часть 5. Алгебра 10 класс.Скачать

Тригонометрическая окружность. Как выучить?Скачать

В какой четверти находится точка единичной окружности, полученная при повороте Ро(1;0) на угол...Скачать

Метод координат для ЕГЭ с нуля за 30 минут.Скачать

Алгебра 10 класс (Урок№29 - Радианная мера угла.)Скачать