Найти координату точки числовой окружности р 61 п 6 (7 видео)

Конспект урока по алгебре 10 класс на тему Числовая окружность на координатной прямой

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов

Сертификат и скидка на обучение каждому участнику

МБОУ Калининская СОШ

анализа 10 класс

«Числовая окружность на координатной плоскости»

Тема Числовая окружность на координатной плоскости

Что будем изучать:
1. Определение.
2. Важные координаты числовой окружности.
3. Как искать координату числовой окружности?
4. Таблица основных координат числовой окружности.
5. Примеры решения задач.
Определение числовой окружности на координатной плоскости

Расположим числовую окружность в координатной плоскости так, чтобы центр окружности совместился с началом координат, а её радиус принимаем за единичный отрезок. Начальная точка числовой окружности A совмещена с точкой (1;0).
Каждая точка числовой окружности имеет в координатной плоскости свои координаты х и у, причем:
1) при x>0x>0, у>0у>0 – в первой четверти;
2) при х 0у>0 – во второй четверти;
3) при х 0х>0, у Запомните уравнение числовой окружности: x2+y2=1×2+y2=1 .

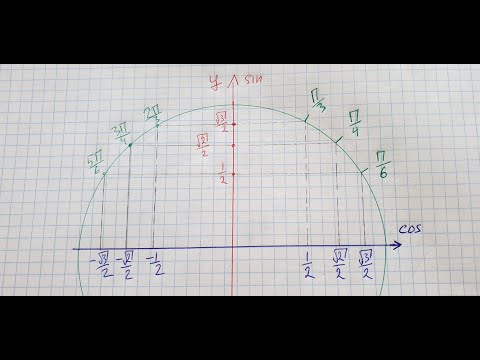
Нам важно научиться находить координаты точек числовой окружности, представленных на рисунке.

Найдем координату точки π4π4

Точка М(π4)М(π4) – середина первой четверти. Опустим из точки М перпендикуляр МР на прямую ОА и рассмотрим треугольник OMP.Так как дуга АМ составляет половину дуги АВ, то ∠ MOP=45° ∠ MOP=45°.
Значит, треугольник OMP – равнобедренный прямоугольный треугольник и OP=MPOP=MP, т.е. у точки M абсцисса и ордината равны: x=yx=y.
Так как координаты точки M(х;y)M(х;y) удовлетворяют уравнению числовой окружности, то для их нахождения нужно решить систему уравнений:
<x2+y2=1,x=y.<x2+y2=1,x=y.
Решив данную систему, получаем: y=x=√22y=x=22.
Значит, координаты точки M, соответствующей числу π4π4, будут M(π4)=M(√22;√22)M(π4)=M(22;22).
Аналогичным образом рассчитываются координаты точек, представленных на предыдущем рисунке.
Координаты точек числовой окружности

Пример 1.
Найти координату точки числовой окружности: Р(45π4)Р(45π4).
Решение:
Т.к. числам tt и t+2π ∗ kt+2π ∗ k, где k-целое число, соответствует одна и та же точка числовой окружности то:
45π4=(10+54) ∗ π=10π+5π4=5π4+2π ∗ 545π4=(10+54) ∗ π=10π+5π4=5π4+2π ∗ 5.
Значит, числу 45π445π4 соответствует та же точка числовой окружности, что и числу 5π45π4. Посмотрев значение точки 5π45π4 в таблице, получаем: P(45π4)=P(−√22;−√22)P(45π4)=P(−22;−22).
Пример 2.
Найти координату точки числовой окружности: Р(−37π3)Р(−37π3).
Решение:
Т.к. числам tt и t+2π ∗ kt+2π ∗ k, где k-целое число, соответствует одна и та же точка числовой окружности то:
−37π3=−(12+13) ∗ π=−12π–π3=−π3+2π ∗ (−6)−37π3=−(12+13) ∗ π=−12π–π3=−π3+2π ∗ (−6).
Значит, числу −37π3−37π3 соответствует та же точка числовой окружности, что и числу –π3–π3, а числу –π3π3 соответствует та же точка, что и 5π35π3. Посмотрев значение точки 5π35π3 в таблице, получаем:
P(−37π3)=P(12;−√32)P(−37π3)=P(12;−32).
Пример 3.
Найти на числовой окружности точки с ординатой у=12у=12 и записать, каким числам tt они соответствуют?
Решение:
Прямая у=12у=12 пересекает числовую окружность в точках М и Р. Точка М соответствует числу π6π6 (из данных таблицы). Значит, и любому числу вида: π6+2π ∗ kπ6+2π ∗ k. Точка Р соответствует числу 5π65π6, а значит, и любому числу вида 5π6+2π ∗ k5π6+2π ∗ k.
Получили, как часто говорят в таких случаях, две серии значений:
π6+2π ∗ kπ6+2π ∗ k и 5π6+2π ∗ k5π6+2π ∗ k.
Ответ : t=π6+2π ∗ kt=π6+2π ∗ k и t=5π6+2π ∗ kt=5π6+2π ∗ k.

Пример 4.
Найти на числовой окружности точки с абсциссой x≥−√22x≥−22 и записать, каким числам ttони соответствуют.

Прямая x=−√22x=−22 пересекает числовую окружность в точках М и Р. Неравенству x≥−√22x≥−22соответствуют точки дуги РМ. Точка М соответствует числу 3π43π4 (из данных таблицы). Значит, и любому числу вида −3π4+2π ∗ k−3π4+2π ∗ k. Точка Р соответствует числу −3π4−3π4, а значит, и любому числу вида −3π4+2π ∗ k−3π4+2π ∗ k.

Тогда получим −3π4+2π ∗ k≤t≤3π4+2πk−3π4+2π ∗ k≤t≤3π4+2πk.

Ответ : −3π4+2π ∗ k≤t≤3π4+2πk−3π4+2π ∗ k≤t≤3π4+2πk.
Задачи для самостоятельного решения

Найти координату точки числовой окружности: Р(61π6)Р(61π6).
2) Найти координату точки числовой окружности: Р(−52π3)Р(−52π3).
3) Найти на числовой окружности точки с ординатой у=−12у=−12 и записать, каким числам ttони соответствуют.
4) Найти на числовой окружности точки с ординатой у≥−12у≥−12 и записать, каким числам ttони соответствуют.
5) Найти на числовой окружности точки с абсциссой x≥−√32x≥− 32 и записать, каким числам t t

Домашние задание: красн. учебник § 5, №5.5
№ 5.7-5.8(в,г), №5.10, №5.12-5.13(в,г)

Содержание

Школе NET
Register
Login
Newsletter
Энджелл
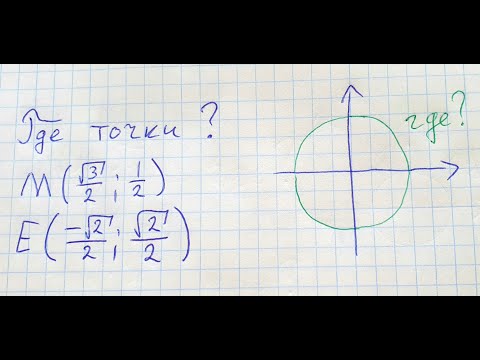
Найди координаты точки числовой окружности P(π/6) = ПОЖАЛУЙСТА помогите
Числовая окружность
Длина числовой окружности равна (2π) или примерно (6,28).
Какие точки соответствуют числам (1), (2) и т.д?
Чтобы отметить на числовой окружности точку соответствующую числу 1, нужно от 0 пройти расстояние равное радиусу в положительном направлении.
Главное свойство числовой окружности
Одному числу на числовой окружности соответствует одна точка, но одной точке соответствует множество чисел.
Все значения одной точки на числовой окружности можно записать с помощью формулы:
🌟 Видео

Видео:Как искать точки на тригонометрической окружности.Скачать

Школе NET

Register

Do you already have an account? Login

Don’t you have an account yet? Register

Submit to our newsletter to receive exclusive stories delivered to you inbox!

Главная 
Вопросы & Ответы 
Вопрос 5650550

Энджелл

Видео:10 класс, 11 урок, Числовая окружностьСкачать

Найди координаты точки числовой окружности P(π/6) = ПОЖАЛУЙСТА помогите

Видео:Координаты точек на числовой окружности, часть 6. Алгебра 10 класс.Скачать

Числовая окружность

В этой статье мы очень подробно разберем определение числовой окружности, узнаем её главное свойство и расставим числа 1,2,3 и т.д. Про то, как отмечать другие числа на окружности (например, (frac, frac, frac, 10π, -frac)) разбирается в этой статье .

Числовой окружностью называют окружность единичного радиуса, точки которой соответствуют действительным числам , расставленным по следующим правилам:

1) Начало отсчета находится в крайней правой точке окружности;

2) Против часовой стрелки — положительное направление; по часовой – отрицательное;

3) Если в положительном направлении отложить на окружности расстояние (t), то мы попадем в точку со значением (t);

4) Если в отрицательном направлении отложить на окружности расстояние (t), то мы попадем в точку со значением (–t).

Почему окружность называется числовой?
Потому что на ней обозначаются числа. В этом окружность похожа на числовую ось – на окружности, как и на оси, для каждого числа есть определенная точка.

Зачем знать, что такое числовая окружность?
С помощью числовой окружности определяют значение синусов, косинусов, тангенсов и котангенсов. Поэтому для знания тригонометрии и сдачи ЕГЭ на 60+ баллов, обязательно нужно понимать, что такое числовая окружность и как на ней расставить точки.

Что в определении означают слова «…единичного радиуса…»?
Это значит, что радиус этой окружности равен (1). И если мы построим такую окружность с центром в начале координат, то она будет пересекаться с осями в точках (1) и (-1).

Ее не обязательно рисовать маленькой, можно изменить «размер» делений по осям, тогда картинка будет крупнее (см. ниже).

Почему радиус именно единица? Так удобнее, ведь в этом случае при вычислении длины окружности с помощью формулы (l=2πR) мы получим:

Длина числовой окружности равна (2π) или примерно (6,28).

А что значит «…точки которой соответствуют действительным числам»?
Как говорили выше, на числовой окружности для любого действительного числа обязательно найдется его «место» — точка, которая соответствует этому числу.

Зачем определять на числовой окружности начало отсчета и направления?
Главная цель числовой окружности — каждому числу однозначно определить свою точку. Но как можно определить, где поставить точку, если неизвестно откуда считать и куда двигаться?

Тут важно не путать начало отсчета на координатной прямой и на числовой окружности – это две разные системы отсчета! А так же не путайте (1) на оси (x) и (0) на окружности – это точки на разных объектах.

Видео:10 класс, 12 урок, Числовая окружность на координатной плоскостиСкачать

Какие точки соответствуют числам (1), (2) и т.д?

Помните, мы приняли, что у числовой окружности радиус равен (1)? Это и будет нашим единичным отрезком (по аналогии с числовой осью), который мы будем откладывать на окружности.

Чтобы отметить на числовой окружности точку соответствующую числу 1, нужно от 0 пройти расстояние равное радиусу в положительном направлении.

Чтобы отметить на окружности точку соответствующую числу (2), нужно пройти расстояние равное двум радиусам от начала отсчета, чтобы (3) – расстояние равное трем радиусам и т.д.

При взгляде на эту картинку у вас могут возникнуть 2 вопроса:
1. Что будет, когда окружность «закончится» (т.е. мы сделаем полный оборот)?
Ответ: пойдем на второй круг! А когда и второй закончится, пойдем на третий и так далее. Поэтому на окружность можно нанести бесконечное количество чисел.

2. Где будут отрицательные числа?
Ответ: там же! Их можно так же расставить, отсчитывая от нуля нужное количество радиусов, но теперь в отрицательном направлении.

К сожалению, обозначать на числовой окружности целые числа затруднительно. Это связано с тем, что длина числовой окружности будет равна не целому числу: (2π). И на самых удобных местах (в точках пересечения с осями) тоже будут не целые числа, а доли числа (π) : ( frac),(-frac),(frac), (2π). Поэтому при работе с окружностью чаще используют числа с (π). Обозначать такие числа гораздо проще (как это делается можете прочитать в этой статье ).

Видео:Координаты точек на числовой окружности, часть 5. Алгебра 10 класс.Скачать

Главное свойство числовой окружности

Одному числу на числовой окружности соответствует одна точка, но одной точке соответствует множество чисел.

Такая вот математическая полигамия.

И следствие из этого правила:

Все значения одной точки на числовой окружности можно записать с помощью формулы:

Если хотите узнать логику этой формулы, и зачем она нужна, посмотрите это видео .

В данной статье мы рассмотрели только теорию о числовой окружности, о том как расставляются точки на числовой и окружности и принципе, как с ней работать вы можете прочитать здесь .

Что надо запомнить про числовую окружность: