Геометрия | 5 — 9 классы
Найдите угол CBA на всех рисунках.
Решить с Дано, найти, решение.
ПОМОГИТЕ заранее спасибо.
1. ΔАВС равнобедренный, значит углы при основании АС равны.
∠СВА = ∠САВ = (180° — 30°) / 2 = 75°
ΔABD — равнобедренный, значит углы при основании AD равны.
∠СВА — внешний, значит равен сумме двух внутренних, не смежных с ним.
∠СВА = ∠BAD + ∠BDA = 140°.
3. ΔBMN равнобедренный, значит углы при основании NM равны.
∠MBN = 180° — (75° + 75°) = 30°
∠CBA = ∠MBN = 30° как вертикальные.
4. ΔABD равнобедренный, ВМ медиана, проведенная к основанию AD, а значит и высота.
∠СВА — внешний для треугольника МВА, значит равен сумме двух внутренних, не смежных с ним.
∠СВА = ∠ВАМ + ∠ВМА = 45° + 90° = 135°
ΔDBC равнобедренный, значит углы при основании СD равны.
∠CDB = 180° — (40° + 40°) = 100°
ВА — медиана равнобедренного треугольника, значит и биссектриса.
∠СВА = ∠CBD / 2 = 100° / 2 = 50°
СК — медиана равнобедренного треугольника CBD, проведенная к основанию BD, а значит и высота.
∠СВА — внешний для треугольника СКВ, значит равен сумме двух внутренних, не смежных с ним.
∠СВА = ∠ВКС + ∠ВСК = 30° + 90° = 120°
ВА — медиана равнобедренного треугольника АСD, проведенная к основанию СD, а значит и высота.
ΔЕBD — равнобедренный, значит углы при основании ЕD равны.
∠ЕBD = 180° — (70° + 70°) = 40°
∠СВА = ∠ЕBD = 40° как вертикальные.
- Надо найти угол CBA помогитеееее?
- Найдите угол CBA заранее спасибо?
- Помогите найти площадь равнобедренногоо треугольника?
- Чему равен угол CBA?
- По данным рисунка найти угол B помогите срочно?
- Здравствуйте?
- У меня 2 задачки для вас))?
- Помогите пожалуйста решить?
- Помогите решить задания под номером : 5, 6, 7 Найдите угол CBA ?
- По данным рисунка найдите угол 1?
- Найдите угол сба равнобедренного треугольника
- Как написать хороший ответ?
- Равнобедренный треугольник. Онлайн калькулятор
- Определение равнобедренного треугольника
- Теорема о равнобедренном треугольнике
- Свойства равнобедренного треугольника
- Признаки равнобедренного треугольника
- 1. Признак равенства равнобедренных треугольников по основанию и боковой стороне
- 2. Признак равенства равнобедренных треугольников по боковой стороне и углу при вершине
- 3. Признак равенства равнобедренных треугольников по основанию и углу при основании
- Задачи и решения
Видео:№227. Найдите углы равнобедренного треугольника, если: а) угол при основании в два разаСкачать

Надо найти угол CBA помогитеееее?
Надо найти угол CBA помогитеееее.
Видео:№228. Найдите углы равнобедренного треугольника, если один из его углов равен: а) 40°Скачать

Найдите угол CBA заранее спасибо?
Найдите угол CBA заранее спасибо!
Видео:№254. Найдите углы равнобедренного прямоугольного треугольника.Скачать

Помогите найти площадь равнобедренногоо треугольника?
Помогите найти площадь равнобедренногоо треугольника.
Если основание равно 12 см а противоположный ему угол = 60 градусов.
Больше данных нет.
Желательно с решением.
Видео:7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать

Чему равен угол CBA?
Чему равен угол CBA?
Если можно с решением.
Видео:№234. Один из внешних углов равнобедренного треугольника равен 115°. Найдите углы треугольника.Скачать

По данным рисунка найти угол B помогите срочно?
По данным рисунка найти угол B помогите срочно!
Видео:Найти угол равнобедренного треугольникаСкачать

Здравствуйте?
Помогите пожалуйста решить задачку по геометрии.
Нужно найти угол CBA.
. Папа решить не смог .
Видео:Определение угла равнобедренного треугольникаСкачать
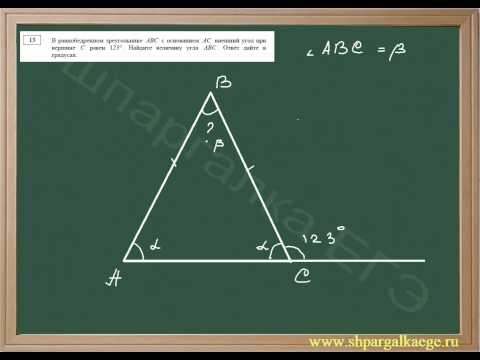
У меня 2 задачки для вас))?
У меня 2 задачки для вас)).
1)На рисунке угол ABC = 70 градусов.
Найдите угол AKC
2)Дан прямоугольник ABCD.
Угол CAB = 30 градусов.
Найдите периметр прямоугольника.
(Рисунки во вложениях).
Видео:Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать

Помогите пожалуйста решить?
Помогите пожалуйста решить.
С рисунком и подробным решением.
Видео:№235. В равнобедренном треугольнике ABC с основанием АС проведена биссектриса AD. Найдите углыСкачать

Помогите решить задания под номером : 5, 6, 7 Найдите угол CBA ?
Помогите решить задания под номером : 5, 6, 7 Найдите угол CBA .
Решение оформить с подробной записью (Дано, Найти, Решение ).
Видео:№259. Угол, противолежащий основанию равнобедренного треугольника, равен 120°. Высота, проведеннаяСкачать

По данным рисунка найдите угол 1?
По данным рисунка найдите угол 1.
Вы перешли к вопросу Найдите угол CBA на всех рисунках?. Он относится к категории Геометрия, для 5 — 9 классов. Здесь размещен ответ по заданным параметрам. Если этот вариант ответа не полностью вас удовлетворяет, то с помощью автоматического умного поиска можно найти другие вопросы по этой же теме, в категории Геометрия. В случае если ответы на похожие вопросы не раскрывают в полном объеме необходимую информацию, то воспользуйтесь кнопкой в верхней части сайта и сформулируйте свой вопрос иначе. Также на этой странице вы сможете ознакомиться с вариантами ответов пользователей.
И так рассмотрим треугольник АВЕ — равнобедренный ВЕ = ВF тогда P = (BF * 6 + 4BF) = 10BF = 88 AB = 2BF = 88 5.
По условию периметр АВСD = R + R + R + 2R = 5R / 60. R = 60 / 5 = 12 см. АD = 2R = 12·2 = 24 см. См. фото.
Отрезки диагоналей в параллелограмме попарно равны, поэтому AO = CO = 12см, а DO = BO = 9 см. Тогда Paob = AO + BO + AB = 12 + 9 + 15 = 21 + 15 = 36 см Ответ : 36 см.
Доказать равенство треугольников ВМА и КСД : углы ВАМ и КСД расвны по условию, стороны АВ = СД как стороны параллелограмма, углы АВМ и КДС равны на внутренние накреслежащие припараллельных ВС и АД.
Vкуба = a³a³ = 3000√3a = ∛(3000√3) = 10∛(3√3) = 10∛(√27) = 10√3Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений. А для квадрата : d² = 3a² = 3 · 300 = 900d = 30.
BD = 36 * 2 = 72 т. К в прямоугольном треугольнике катет, лежащий напротив угла в 30 градусов, равен половине гипотенузы.
При пересечении двух прямых образуется 4 угла и их сумма равна 360°. Если сумма трёх из них равна 306° , то градусная мера четвёртого угла равна 360 — 306 = 54°. Смежный с ним угол равен 180 — 54 = 126° — это и есть больший из них.
Дано : Решение : АО = 21 см Т. К. по условию задачи CD = 56 см отрезки АВ и CD P = 83 см разделены т. О пополам, Найти : то СО = 56 / 2 = 28 BD — ? Рассмотрим треугольники АОС и ОBD : 1) AO = OB по условию ; 2)CO = OD по условию ; 3)угол AOC = уго..
38 см 5 мм вот вроде так.
1. Была какая — то теорема для быстрого решения подобной задачи, но я ее не помню, так что так Рассмотрим треугольники МКО и МНО угол ОМК = углу ОМН по условию МК — общая НОМ = 180 — (ОНМ = НМО), КОМ = 180 — (ОКМ — КМО), тк ОКМ = ОНМ = > НОМ = КОМ Из..
Видео:№263. Высоты, проведенные к боковым сторонам АВ и АС остроугольного равнобедренного треугольникаСкачать

Найдите угол сба равнобедренного треугольника
Вопрос по геометрии:
Помогите пожалуйста решить задачи
свойства равнобедренного треугольника
найти угол:cba
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!
Ответы и объяснения 1
Знаете ответ? Поделитесь им!
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
- Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
- Писать без грамматических, орфографических и пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
- Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
- Использовать мат — это неуважительно по отношению к пользователям;
- Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Геометрия.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!
Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.
Видео:№225. Докажите, что каждый угол равностороннего треугольника равен 60°.Скачать

Равнобедренный треугольник. Онлайн калькулятор
С помощю этого онлайн калькулятора можно найти неизвестные элементы (стороны, углы) а также периметр, площадь, высоты равнобедренного треугольника. Теоретическую часть и численные примеры смотрите ниже.
| Открыть онлайн калькулятор |
Видео:Равнобедренный треугольник. 7 класс.Скачать

Определение равнобедренного треугольника
Определение 1 (Евклид). Треугольник, в котором длины двух сторон равны между собой называется равнобедренным треугольником.
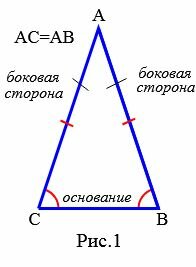
Равные стороны равнобедренного трекугольника называются боковыми сторонами. Третья сторона равнобедренного треугольника называется основанием треугольника (Рис.1).
Угол между боковыми сторонами равнобедненного треугольника (( small angle A ) ) называется вершинным углом. Углы между основанием и боковыми сторонами (( small angle B, angle C ) ) называются углами при основании.
 |
Существует более общее определение равнобедненого треугольника:
Определение 2 (Современная трактовка). Треугольник, в котором длины хотя бы двух сторон равны между собой называется равнобедренным треугольником.
Из определения 2 следует, что равносторонний треугольник является частным случаем равнобедренного треугольника. Действительно, в качестве равных сторон можно взять любые две стороны равностороннего треугольника, а третья сторона будет основанием.
Видео:Вариант 28, № 4. Равнобедренный треугольник. Угол при вершинеСкачать

Теорема о равнобедренном треугольнике
Теорема 1. Углы, прилежащие к основанию равнобедренного треугольника равны.
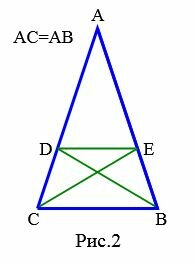 |
Доказательство (доказательство Прокла). Пусть задан равнобедренный треугольник ABC, где AB=AC (Рис.2). Докажем, что ( small angle B= angle C. ) Возьмем любую точку D на стороне AC и точку E на стороне AB так, чтобы AD=AE. Проведем отрезки DE, CE, BD. Треугольники ABD и ACE равны по двум сторонам и углу между ними: AE=AD, AC=AB, угол ( small angle A ) общий (см. статью на странице Треугольники. Признаки равенства треугольников). Отсюда следует:
| ( small CE=BD,) | (1) |
| ( small angle ACE=angle ABD.) | (2) |
Из ( small AB=AC) и ( small AD=AE ) следует:
| ( small CD=BE.) | (3) |
Рассмотрим треугольники CBE и BCD. Они равны по трем сторонам: ( small CE=BD,) ( small CD=BE ,) сторона ( small BC ) общая. Отсюда следует, что
| ( small angle ECB= angle DBC. ) | (4) |
Из (2) и (4) следует, что ( small angle B= angle C. )
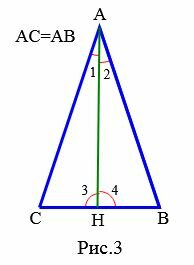 |
Доказательство (Вариант 2). Пусть задан равнобедренный треугольник ABC, где AB=AC (Рис.3). Проведем биссектрису ( small AH ) треугольника. Тогда ( small angle CAH=angle BAH. ) Докажем, что ( small angle B= angle C. ) Треугольники AHB и AHC равны по двум сторонам и углу между ними: AC=AB, сторона ( small AH ) общая, ( small angle CAH=angle BAH. ) Отсюда следует: ( small angle B= angle C. )
Видео:Найдите угол: задача по геометрииСкачать

Свойства равнобедренного треугольника
Теорема 2. В равнобедренном треугольнике биссектриса проведенная к основанию является медианой и высотой.
Доказательство. Рассмотрим равнобедренный треугольник ABC, где AB=AC, а AH− биссектриса треугольника (Рис.3). Треугольники AHB и AHC равны по двум сторонам и углу между ними: AC=AB, сторона ( small AH ) общая, ( small angle 1=angle 2. ) Тогда ( small CH=HB, ) ( small angle 3=angle 4. ) Равенство ( small CH=HB ) означает, что ( small AH ) является также медианой треугольника ABC. Углы ( small angle 3) и ( angle 4 ) смежные. Следовательно их сумма равна 180° и, поскольку эти углы равны, то каждый из этих углов равен 90°. Тогда ( small AH ) является также высотой треугольника ( small ABC. ) Поскольку высота ( small AH ) перпендикулярна к ( small BC ) и ( small CH=HB, ) то ( small AH ) является также серединным перпендикуляром к основанию равнобедренного треугольника.
Мы доказали, что биссектриса, медиана, высота и серединный перпендикуляр равнобедренного треугольника, проведенные к основанию совпадают.
Исходя из теоремы 2 можно сформулировать следующие теоремы, доказательство которых аналогично доказательству теоремы 2:
Теорема 3. В равнобедренном треугольнике медиана проведенная к основанию является биссектрисой и высотой.
Теорема 4. В равнобедренном треугольнике высота проведенная к основанию является биссектрисой и медианой.
Видео:Свойства равнобедренного треугольника. 7 класс.Скачать

Признаки равнобедренного треугольника
Признак 1. Если в треугольнике две стороны равны, то треугольник является равнобедренным.
Признак 1 следует из определения 1.
Признак 2. Если в треугольнике два угла равны, то треугольник является равнобедренным.
Доказательство признака 2 смотрите в статье Соотношения между сторонами и углами треугольника (Следствие 2. Признак равнобедренного треугольника).
Признак 3. Если в треугольнике высота проведенная к одной стороне совпадает с медианой проведенной к этой же стороне, то треугольник является равнобедренным.
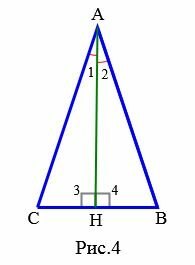
Доказательство. Пусть в треугольнике ( small ABC ) ( small AH ) является высотой и медианой (Рис.4). Тогда ( small angle 3=angle4=90°, ) ( small CH=HB. ) Треугольники ( small AHC ) и ( small AHB ) равны по двум сторонам и углу между ними (первый признак равенства треугольников): ( small AH ) − общая сторона, ( small CH=HB, ) ( small angle 3=angle4. ) Следовательно ( small AB=AC. )
Признак 4. Если в треугольнике высота проведенная к одной стороне совпадает с биссектрисой проведенной к этой же стороне, то треугольник является равнобедренным.
Доказательство. Пусть в треугольнике ( small ABC ) ( small AH ) является высотой и биссектрисой (Рис.4). Тогда ( small angle 3=angle4=90°, ) ( small angle 1=angle2. ) Треугольники ( small AHC ) и ( small AHB ) равны по стороне и прилежащим двум углам (второй признак равенства треугольников): ( small AH ) − общая сторона, ( small angle 1=angle 2, ) ( small angle 3=angle4. ) Следовательно ( small AB=AC. )
  |
Признак 5. Если в треугольнике биссектриса проведенная к одной стороне совпадает с медианой проведенной к этой же стороне, то треугольник является равнобедренным.
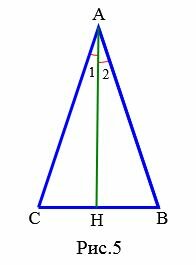
Доказательство (Вариант 1). Пусть в треугольнике ( small ABC ) ( small AH ) является биссектрисой и медианой (Рис.5). Тогда
| ( small angle 1=angle2, ) ( small CH=HB. ) | (5) |
Применим теорему синусов для треугольника ( small AHC ):
| ( small frac = frac . ) | (6) |
Применим теорему синусов для треугольника ( small AHB ):
| ( small frac = frac . ) | (7) |
тогда, из (5), (6), (7) получим:
| ( small frac = frac . ) | (8) |
Следовательно ( small sin angle C= sin angle B. ) Поскольку сумма всех углов треугольника равна 180°, то нам интересует синус углов от 0 до 180°. Учитывая это получим, что синусы углов равны в двух случаях: 1) ( small angle C= angle B, ) 2) ( small angle C= 180° — angle B. ) Поскольку сумма двух углов треугольника меньше 180°: ( small angle C + angle B Доказательство (Вариант 2). Пусть в треугольнике ( small ABC ) ( small AH ) является биссектрисой и медианой, т.е. ( small angle 1=angle 2, ) ( small CH=HB ) (Рис.6). На луче ( small AH ) отложим отрезок ( small HD ) так, чтобы ( small AH=HD. ) Соединим точки ( small C ) и ( small D. )
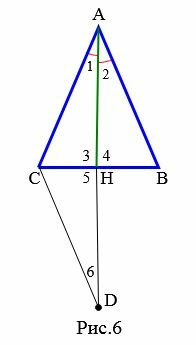 |
Треугольники ( small AHB ) и ( small DHC ) равны по двум сторонам и углу между ними (первый признак равенства треугольников). Действительно: ( small AH=HD, ) ( small CH=HB, ) ( small angle 4=angle 5 ) (углы 4 и 5 вертикальные). Тогда ( small AB=CD, ) ( small angle 6=angle 2. ) Отсюда ( small angle 6=angle 1. ) Получили, что треугольник ( small CAD ) равнобедренный (признак 2). Тогда ( small AC=CD. ) Но ( small AB=CD ) и, следовательно ( small AB=AC. ) Получили, что треугольник ( small ABC ) равнобедренный.
Видео:Один из внешних углов равнобедренного треугольника равен 80 градусов Найдите углы этого треугольникСкачать

1. Признак равенства равнобедренных треугольников по основанию и боковой стороне
Если основание и боковая сторона одного равнобедренного треугольника соответственно равны основанию и боковой стороне другого равнобедненного треугольника, то эти треугольники равны.
Действительно. Поскольку треугольник равнобедренный, то боковые стороны равны. То есть три стороны одного равнобедренного треугольника соответственно равны трем сторонам другого равнобедненного треугольника. А по третьему признаку равенства треугольников, эти треугольники равны.
Видео:Геометрия 7 класс (Урок№13 - Равнобедренный треугольник.)Скачать

2. Признак равенства равнобедренных треугольников по боковой стороне и углу при вершине
Если боковая сторона и угол при вершине одного равнобедренного треугольники соответственно равны боковой стороне и углу при вершине другого равнобедренного треугольника, то такие треугольники равны.
Действительно. Так как боковые стороны равнобедненного треугольника равны, то имеем: две стороны и угол между ними одного треугольника соотвественно равны двум сторонам и углу между ними другого треугольника. Тогда по первому признаку равенства треугольников, эти реугольники равны.
Видео:Только 1 может решить эту хитрую задачу ★ Найдите углы треугольника ★ Супер ЖЕСТЬСкачать

3. Признак равенства равнобедренных треугольников по основанию и углу при основании
Если основание и угол при основании равнобедренного треугольника соответственно равны основанию и углу при основании другого равнобедренного треугольника, то такие треугольники равны.
Доказательство. В равнобедренном треугольнике углы при основании равны. тогда имеем: основание и две углы одного равнобедненного треугольника равны основанию и двум углам другого равнобедненного треугольника. Тогда эти треугольники равны по второму признаку равенства треугольников.
Видео:Учимся решать задачи по геометрии. Равнобедренный треугольникСкачать

Задачи и решения
Задача 1. Известны основание ( small a=5 ) и высота ( small h=6 ) равнобедренного треугольника. Найти углы, боковые стороны, периметр, площадь.
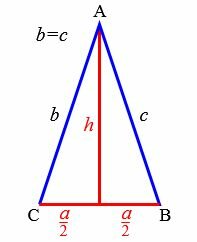 |
Решение. Найдем боковые стороны ( small b ) и ( small c ) равнобедренного треугольника. Воспользуемся теоремой Пифагора:
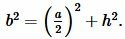 |
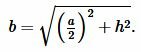 | (9) |
Подставляя значения ( small a ) и ( small h ) в (9), получим:
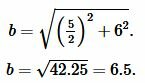 |
Боковая сторона ( small c ) равнобедренного треугольника равна:
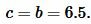 |
Найдем периметр треугольника. Периметр треугольника равен сумме длин его сторон:
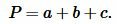 | (10) |
Подставляя значения ( small a=5, ) ( small b=6.5 ) и ( small c=6.5 ) в (10), получим:
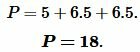 |
Найдем угол ( small B ) равнобедренного треугольника:
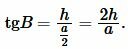 | (11) |
Подставляя значения ( small a=5, ) ( small h=6 ) в (11), получим:
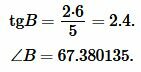 |
Тогда угол ( small C ) равнобедренного треугольника равен:
 |
Поскольку сумма всех углов треугольника равна 180°, то имеем:
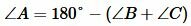 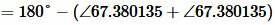 , , |
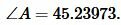 |
Площадь треугольника можно вычислить из формулы:
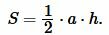 | (12) |
Подставляя значения ( small a=5, ) ( small h=6 ) в (12), получим: