Найдите угол х если прямые параллельны (4 видео)

Угол между прямыми онлайн

С помощью этого онлайн калькулятора можно найти угол между прямыми. Дается подробное решение с пояснениями. Для вычисления угла между прямыми, задайте размерность (2-если рассматривается прямая на плоскости, 3- если рассматривается прямая в пространстве), выберите вид уравнения (канонический, параметрический, общий (для двухмерного пространства)), введите данные в ячейки и нажмите на кнопку «Решить». Теоретическую часть и численные примеры смотрите ниже.

Содержание

Предупреждение
1. Угол между прямыми на плоскости
Прямые заданы каноническими уравнениями
1.1. Определение угла между прямыми
1.2. Условие параллельности прямых
1.3. Условие перпендикулярности прямых
Прямые заданы общими уравнениями
1.4. Определение угла между прямыми
1.5. Условие параллельности прямых
1.6. Условие перпендикулярности прямых
2. Угол между прямыми в пространстве
2.1. Определение угла между прямыми
2.2. Условие параллельности прямых
2.3. Условие перпендикулярности прямых
Решение задач по теме «Параллельные прямые»
Угол между прямыми
🔍 Видео

Предупреждение

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

Видео:Найдите угол ХСкачать

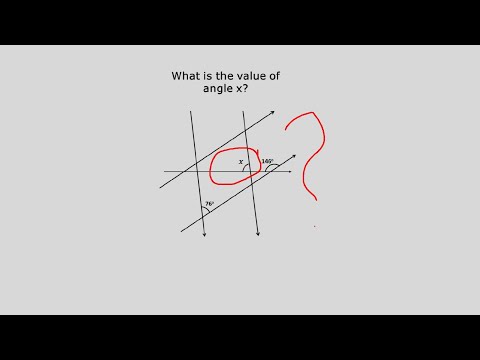
1. Угол между прямыми на плоскости

Прямые заданы каноническими уравнениями

1.1. Определение угла между прямыми

Пусть в двухмерном пространстве прямые L₁ и L₂ заданы каноническими уравнениями

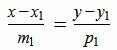(1.1)

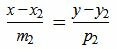(1.2)

Задача об определении угла между прямыми L₁ и L₂ сводится к задаче об определении угла между направляющими векторами q₁ и q₂ (рис.1).

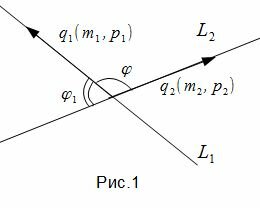(1.3)

Из выражения (1.3) получим:

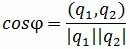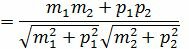(1.4)

Таким образом, из формулы (1.4) можно найти угол между прямыми L₁ и L₂. Как видно из Рис.1 пересекающиеся прямые образуют смежные углы φ и φ₁. Если найденный угол больше 90°, то можно найти минимальный угол между прямыми L₁ и L₂: φ₁=180-φ.

Из формулы (1.4) можно вывести условия параллельности и перпендикулярности двух прямых.

Пример 1. Определить угол между прямыми

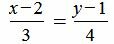(1.5)

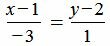(1.6)

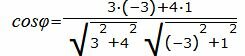Упростим и решим:

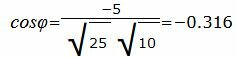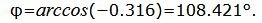Данный угол больше 90°. Найдем минимальный угол между прямыми. Для этого вычтем этот угол из 180:

Угол между прямыми равен:

1.2. Условие параллельности прямых

Пусть φ=0. Тогда cosφ=1. При этом выражение (1.4) примет следующий вид:

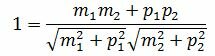(1.7)

Сделаем преобразования с выражением (1.7):

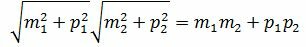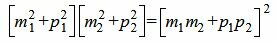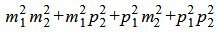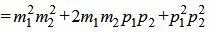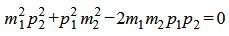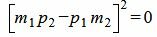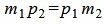(1.8)

Таким образом условие параллельности прямых L₁ и L₂ имеет вид (1.8). Если m₂≠0 и p₂≠0, то (1.8) можно записать так:

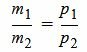(1.9)

Пример 2. Определить, параллельны ли прямые

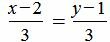(1.10)

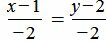(1.11)

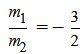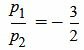Удовлетворяется равенство (1.9), следовательно прямые (1.10) и (1.11) параллельны.

Ответ. Прямые (1.10) и (1.11) параллельны.

1.3. Условие перпендикулярности прямых

Пусть φ=90°. Тогда cosφ=0. При этом выражение (1.4) примет следующий вид:

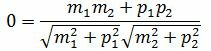(1.12)

Правая часть выражения (1.12) равно нулю тогда и только тогда, когда числитель равен нулю. Следовательно, для того, чтобы прямые L₁ и L₂ были перпендикулярны , должно выполняться условие

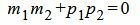(1.13)

Пример 3. Определить, перпендикулярны ли прямые

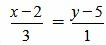(1.14)

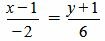(1.15)

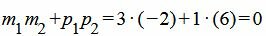(16)

Удовлетворяется условие (1.13), следовательно прямые (1.14) и (1.15) перпендикулярны.

Ответ. Прямые (1.14) и (1.15) перпендикулярны.

Прямые заданы общими уравнениями

1.4. Определение угла между прямыми

Пусть две прямые L₁ и L₂ заданы общими уравнениями

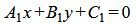(1.17)

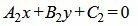(1.18)

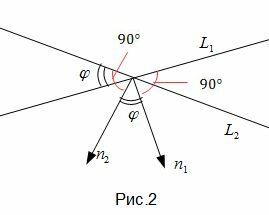
Так как нормальным вектором прямой L₁ является n₁=(A₁, B₁), а нормальным вектором прямой L₂ является n₂=(A₂, B₂), то задача об определении угла между прямыми L₁ и L₂ сводится к определению угла φ между векторами n₁ и n₂ (Рис.2).

Из определения скалярного произведения двух векторов, имеем:

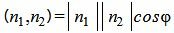(1.19)

Из уравнения (19) получим

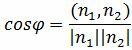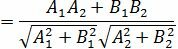(1.20)

Пример 4. Найти угол между прямыми

5x₁−2x₂+3=0

(1.21)

x₁+3x₂−1=0.

(1.22)

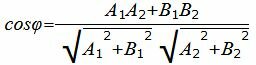(23)

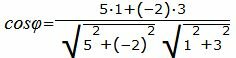Упростим и решим:

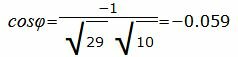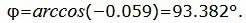Данный угол больше 90°. Найдем минимальный угол между прямыми. Для этого вычтем этот угол из 180:

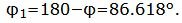1.5. Условие параллельности прямых

Так как угол между паралленьными прямыми равен нулю, то φ=0, cos(φ)=1. Тогда сделав преобразования, представленные выше для канонических уравнений прямых получим условие параллельности:

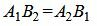(1.24)

С другой стороны условие параллельности прямых L₁ и L₂ эквивалентно условию коллинеарности векторов n₁ и n₂ и можно представить так:

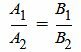(1.25)

Как видим уравнения (1.24) и (1.25) эквивалентны при A₂≠0 и B₂≠0. Если в координатах нормальных векторов существует нулевой коэффициент, то нужно использовать уравнение (1.24).

Пример 5. Определить, параллельны ли прямые

4x+2y+2=0

(1.26)

Удовлетворяется равенство (1.24), следовательно прямые (1.26) и (1.27) параллельны.

Ответ. Прямые (1.26) и (1.27) параллельны.

1.6. Условие перпендикулярности прямых

Условие перпендикулярности прямых L₁ и L₂ можно извлекать из формулы (1.20), подставляя cos(φ)=0. Тогда скалярное произведение (n₁,n₂)=0. Откуда

A₁A₂+B₁B₂=0.

(1.28)

Таким образом условие перпендикулярности прямых определяется равенством (1.28).

Пример 6. Определить, перпендикулярны ли прямые

4x−1y+2=0

(1.29)

2x+8y−14=0.

(1.30)

Удовлетворяется равенство (1.28), следовательно прямые (1.29) и (1.30) перпендикулярны.

Ответ. Прямые (1.29) и (1.30) перпендикулярны.

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

2. Угол между прямыми в пространстве

2.1. Определение угла между прямыми

Пусть в пространстве прямые L₁ и L₂ заданы каноническими уравнениями

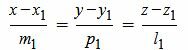(2.1)

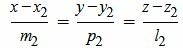(2.2)

Задача об определении угла между прямыми L₁ и L₂ сводится к задаче об определении угла между направляющими векторами q₁ и q₂ .

(2.3)

Из выражения (2.3) получим:

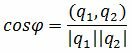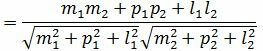(2.4)

Таким образом, из формулы (2.4) можно найти угол между прямыми L₁ и L₂. Если найденный угол больше 90°, то можно найти минимальный угол между прямыми L₁ и L₂: φ₁=180-φ.

Из формулы (2.4) можно вывести условия параллельности и перпендикулярности двух прямых.

Пример 1. Определить угол между прямыми

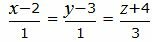(2.5)

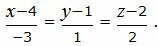(2.6)

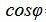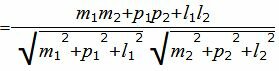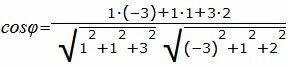Упростим и решим:

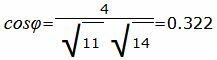Угол между прямыми равен:

2.2. Условие параллельности прямых

Условие параллельности прямых эквивалентно условию коллинеарности направляющих векторов q₁ и q₂, т.е. соответствующие координаты этих векторов пропорциональны. Пусть

m₁=αm₂, p₁=αp₂, l₁=αl₂

(2.7)

где α − некоторое число. Тогда соответствующие координаты векторов q₁ и q₂ пропорциональны, и, следовательно прямые L₁ и L₂ параллельны.

Условие параллельности прямых можно представить и так:

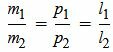(2.8)

Отметим, что любую пропорцию нужно понимать как равенство ad=bc.

Пример 2. Определить, параллельны ли прямые

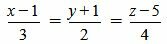(2.9)

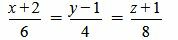(2.10)

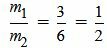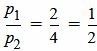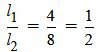Удовлетворяется равенство (2.8) (или (2.7)), следовательно прямые (2.9) и (2.10) параллельны.

Ответ. Прямые (2,9) и (2,10) параллельны.

Пример 3. Определить, параллельны ли прямые

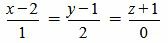(2.11)

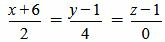(2.12)

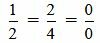(2.13)

Выражение (2.13) нужно понимать так:

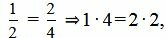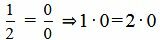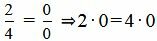(2.14)

Как мы видим из (2.14) условия (2.13) выполняются. Следовательно прямые (2.11) и (2.12) параллельны.

Ответ. Прямые (2.11) и (2.12) параллельны.

2.3. Условие перпендикулярности прямых

Пусть φ=90°. Тогда cosφ=0. При этом выражение (2.4) примет следующий вид:

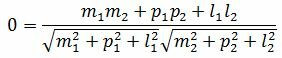(2.15)

Правая часть выражения (2.15) равно нулю тогда и только тогда, когда числитель равен нулю. Следовательно, для того, чтобы прямые L₁ и L₂ были перпендикулярны , должно выполняться условие

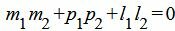(2.16)

Пример 3. Определить, перпендикулярны ли прямые

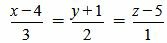(2.17)

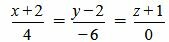(2.18)

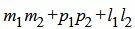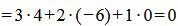(2.19)

Удовлетворяется условие (2.16), следовательно прямые (2.17) и (2.18) перпендикулярны.

Ответ. Прямые (2.17) и (2.18) перпендикулярны.

Видео:Геометрия 7 класс (Урок№19 - Признаки параллельности прямых.)Скачать

Решение задач по теме «Параллельные прямые»

Разделы: Математика

Задачи:

учащиеся группы «А» должны уметь решать базовые задачи по теме «Параллельные прямые», учащиеся группы «В» совершенствуют навыки решения задач по данной теме, учащиеся группы «С» должны уметь применять знания в нестандартной обстановке;
развивать устную и письменную математическую речь, выражать свои мысли, умение работать самостоятельно и в группе, логическое мышление;
воспитывать ответственность, аккуратность, аккуратности в построении чертежей, трудолюбия.

Ход урока

I. Орг. момент

II. Постановка задач урока учащимися

III. Решение задач

Для учащиеся группы «С» — индивидуально-групповая работа

Для учащихся группы «В» — индивидуальная работа

Для учащихся группы «А» — работа с учителем.

Задачи для учащихся группы «А»

назвать внутренние односторонние углы
назвать внутренние накрест лежащие угла
вертикальные углы
смежные
соответственные

Дано:

Какие из прямых а, b с — параллельные?

Прямые а и в параллельны

угол 1 равен 138°. Найти величину остальных углов.
один из двух внутренних односторонних углов на 20° меньше другого. Найти все углы, образованные при пересечении двух параллельных прямых секущей

4. Прямые параллельны, если равны…

а) смежные углы
б) накрест лежащие углы
в) односторонние углы

5. Выяснить взаимное расположение прямых m и n.

После решения задач, учащимся предложить аналогичные задачи для самостоятельного решения. В конце урока тетради сдаются на проверку учителю.

Задачи для учащихся группы «В»

2) У одного человека было трое сыновей. Однажды позвал он их и говорит:

— Слыхал я, что продаются в городе кувшины мудрости. Дно у них параллельно донышку. Кому повезет такой кувшин купить, тот до конца жизни горя знать не будет. Дам я вам по мешочку золота, отправляйтесь в город и постарайтесь купить себе по такому кувшину. Какие кувшины нужно купить братьям?

Задачи для учащихся группы «С»

1. АВ параллельна А₁В₁, АК — биссектриса угла ВАМ, А₁К₁ — биссектриса угла В₁А₁М. Могут ли пересекаться прямые АК и А₁К₁? Почему?

2. ВЕ параллельна ДС. АВ = ВД = ВС.

Доказать: прямая ДС перпендикулярна прямой АС

3*. ВЕ параллельна АК, АВ параллельна ДЕ, АВ = ДС.

4. Прямая АВ параллельна прямой СД, угол СДА равен 20°, угол ДЕВ равен 70°.

Найти величину угла АВС.

5*. Внутри треугольника АВС отмечена точка К. Через нее проведены прямые, параллельные сторонам АС и АВ и пересекающие сторону ВС соответственно в точках М и Е, КМ = МС, КЕ = ЕВ. Докажите, что К – точка пересечения биссектрис

IV. Проверка ответов и разбор задач, вызвавших затруднение, у учащихся группы «В» и «С»

V. Подведение итогов урока.

Наш урок подходит концу. Пожалуйста, поделитесь своими мыслями о этом занятии (хотите одним предложением).

Вам для этого помогут слова:

-У меня получилось…

-У меня сначала вызвало затруднение, а потом…

— Я смогу теперь решить …

VI. Домашнее задание: индивидуальные карточки

VII. Параллельны ли прямые на рисунке?

Видео:Угол между прямыми в пространстве. 10 класс.Скачать

Угол между прямыми

Данный калькулятор предназначен для вычисления угла между двумя прямыми онлайн.

Две прямые могут иметь три варианта взаимного расположения друг к другу. Они могут совпадать, быть параллельны или же пересекаться. Для определения угла между прямыми наиболее интересным случаем является угол между скрещивающимися (или пересекающимися) прямыми.

Если две прямые имеют одну общую точку, то такие прямые называются пересекающимися. Точка пересечения делит каждую из прямых на два луча. Между лучами пересекающихся прямых образовываются четыре угла (два острых и два тупых). Итак, угол между двумя скрещивающимися прямыми – это наименьший угол (острый), образованный при пересечении этих прямых. Следует отметить, что, если известно значение одного из углов, можно легко найти значения остальных трех углов благодаря свойствам вертикальных и смежных углов.

Для того чтобы найти угол между двумя прямыми с помощью данного калькулятора, необходимо ввести коэффициенты в уравнения прямых и нажать кнопку «Вычислить».

Если прямые заданы следующими уравнениями:

тогда направляющие векторы этих прямых будут равны:

Воспользуемся формулой скалярного произведения двух векторов: