С помощю этого онлайн калькулятора можно решить треугольники, т.е. найти неизвестные элементы (стороны, углы) треугольника. Теоретическую часть и численные примеры смотрите ниже.
Решение треугольников − это нахождение всех его элементов (трех сторон и трех углов) по трем известным элементам (сторонам и углам). В статье Треугольники. Признаки равенства треугольников рассматриваются условия, при которых два треугольника оказываются равными друг друга. Как следует из статьи, треугольник однозначно определяется тремя элементами. Это:
- Три стороны треугольника.
- Две стороны треугольника и угол между ними.
- Две стороны и угол противостоящий к одному из этих сторон треугольника.
- Одна сторона и любые два угла.
Заметим, что если у треугольника известны два угла, то легко найти третий угол, т.к. сумма всех углов треугольника равна 180°.
Видео:Найдите сторону треугольника на рисункеСкачать

Решение треугольника по трем сторонам
Пусть известны три стороны треугольника a, b, c (Рис.1). Найдем 
 |
 |
 |
 | (1) |
 | (2) |
Из (1) и (2) находим cosA, cosB и углы A и B (используя калькулятор). Далее, угол C находим из выражения
 . . |
Пример 1. Известны стороны треугольника ABC: 

Решение. Из формул (1) и (2) находим:
  . . |
  . . |
 , ,  . . |
И, наконец, находим угол C:
  |
Видео:По силам каждому ★ Найдите стороны треугольника на рисункеСкачать

Решение треугольника по двум сторонам и углу между ними
Пусть известны стороны треугольника a и b и угол между ними C (Рис.2). Найдем сторону c и углы A и B.
 |
Найдем сторону c используя теорему косинусов:
 . . |
 . . |
Далее, из формулы
 . . |
 . . | (3) |
Далее из (3) с помощью калькулятора находим угол A.
Поскольку уже нам известны два угла то находим третий:
 . . |
Пример 2. Известны две стороны треугольника ABC: 

Решение. Иcпользуя теорму косинусов найдем сторону c:
 , , |
   . . |
Из формулы (3) найдем cosA:
  |
 . . |
Поскольку уже нам известны два угла то находим третий:
  . . |
Видео:Найдите третью сторону треугольникаСкачать

Решение треугольника по стороне и любым двум углам
Пусть известна сторона треугольника a и углы A и B (Рис.4). Найдем стороны b и c и угол C.
 |
Так как, уже известны два угла, то можно найти третий:
 . . |
Далее, для находждения сторон b и c воспользуемся тероемой синусов:
 , ,  . . |
 , ,  . . |
Пример 3. Известна одна сторона треугольника ABC: 

Решение. Поскольку известны два угла, то легко можно найти третий угол С:
  |
Найдем сторону b. Из теоремы синусов имеем:
 |
 |
Найдем сторону с. Из теоремы синусов имеем:
Видео:Найдите сторону треугольника, если другие его стороны равны 1 и 5Скачать

Найдите х в треугольнике
9) Рисунок 1: тр. KML — равнобедренный ( КМ = МL )
▪ Отложим отрезок МN, равный отрезку KM, на её продолжении ***** угол NML = 180° — 120° = 60° ***** тр. NML — равносторонний, то есть на стороне ML построили равносторонний треугольник внешним образом ***** KM = ML = MN = NL = x
▪ По теореме Пифагора в тр. KNL:
KN^2 = KL^2 + NL^2
10) тр. RTS — прямоугольный , угол Т = 90°
▪ По теореме Пифагора в тр. RTS:
RS^2 = RT^2 + TS^2
TS^2 = 13^2 — 12^2
TS^2 = 169 — 144 = 25
TS = 5
▪ Площадь треугольника RTS:
S rts = TM • RS / 2 = RT • TS / 2
TM • RS = RT • TS
TM = RT • TS / RS = 12 • 5 / 13 = 60 / 13 = 4_8/13
11) ▪тр. АСВ — равнобедренный ( АС = СВ )
CD — высота, медиана, биссектриса **** AD = DB = 10/2 = 5
▪ По теореме Пифагора в тр. BCD:
CD^2 = 13^2 — 5^2 = 169 — 25 = 144
CD = 12
▪Плошадь тр. АСВ:
S acb = CD • AB / 2 = AE • CB / 2
CD • AB = AE • CB
AE = CD • AB / CB = 12 • 10 / 13 = 120 / 13 =
9_3/13
12) KMRN — ромб ( KM = MR = RN = KN )
▪Диагонали ромба взаимно перпендикулярны, делящие ромб на 4 равных прямоугольных треугольника. Диагонали ромба точкой пересечения делятся пополам ***** Пусть точка О — точка пересечения диагоналей ромба ***** KO = OR = 10/2 = 5 ***** MO = ON = 12/2 = 6
▪ По теореме Пифагора в тр. МОК:
МК^2 = 5^2 + 6^2 = 25 + 36 = 61
МК = V61
13) АBCD — ромб ( AB = BC = CD = AD )
▪Диагонали ромба взаимно перпендикулярны и точкой пересечения делятся пополам ***** Пусть точка О — точка пересечения диагоналей ромба ***** ВO = OD = 12/2 = 6
▪По теореме Пифагора в тр. ВОС:
ОС^2 = 10^2 — 6^2 = 100 — 36 = 64
ОС = 8
АС = 2•ОС = 2•8 = 16
14)
▪Применим для тр. MNK теорему Пифагора:
MK^2 = MN^2 + NK^2
25^2 = 7^2 + 24^2
625 = 49 + 576
625 = 625
Следовательно, по теореме, обратной теореме Пифагора, следует, что тр. МNK — прямоугольный ( угол N = 90° )
▪ Площадь тр. MNK:
S mnk = NL • MK / 2 = MN • NK / 2
NL • MK = MN • NK
NL = MN • NK / MK = 7 • 24 / 25 = 168/25 = 6,72
15) SRLK — прямоугольник
▪Очевидно, что в этой задаче не хватает данных для её решения
Допустим, что в условии задачи известна сторона KS = 5, тогда
▪ По теореме Пифагора в тр. LKS:
SL^2 = KS^2 + KL^2
SL^2 = 5^2 + 12^2 = 25 + 144 = 169
SL = 13
16)
▪ Применим для тр. МКТ теорему Пифагора:
МТ^2 = КТ^2 + МК^2
34^2 = 30^2 + 16^2
1156 = 900 + 256
1156 = 1156
Значит, по теореме, обратной теореме Пифагора, следует, что тр. МКТ — прямоугольный ( угол К = 90° )
▪Пропорциональные отрезки в прямоугольном треугольнике:
МК^2 = MN • MT
16^2 = MN • 34
256 = MN • 34
MN = 256/34 = 128/17 = 7_9/17
Видео:Математика головоломка геометрия Найти угол х ?Скачать

Решение задач по математике онлайн
//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘
Видео:Сумма углов треугольника. Геометрия 7 класс | МатематикаСкачать

Калькулятор онлайн.
Решение треугольников.
Решением треугольника называется нахождение всех его шести элементов (т.е. трех сторон и трех углов) по каким-нибудь трем данным элементам, определяющим треугольник.
Эта математическая программа находит сторону ( c ), углы ( alpha ) и ( beta ) по заданным пользователем сторонам ( a, b ) и углу между ними ( gamma )
Программа не только даёт ответ задачи, но и отображает процесс нахождения решения.
Этот калькулятор онлайн может быть полезен учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.
Если вы не знакомы с правилами ввода чисел, рекомендуем с ними ознакомиться.
Введите стороны ( a, b ) и угол между ними ( gamma ) Решить треугольник
🎬 Видео
№550. По данным рисунка 193 найдите x и y.Скачать
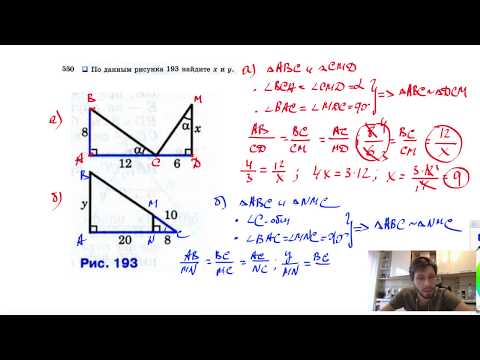
Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Найдите угол: задача по геометрииСкачать

Задача, которую боятсяСкачать

ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать

Супер ЖЕСТЬ ➜ Найдите сторону треугольника ➜ Решить без тригонометрииСкачать

Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Как ПОНЯТЬ ГЕОМЕТРИЮ за 5 минут — Подобие ТреугольниковСкачать

Решение прямоугольных треугольников. Практическая часть. 8 класс.Скачать

Катеты прямоугольного треугольника равны cosx и sin2. Найдите x, если гипотенуза равна 1Скачать
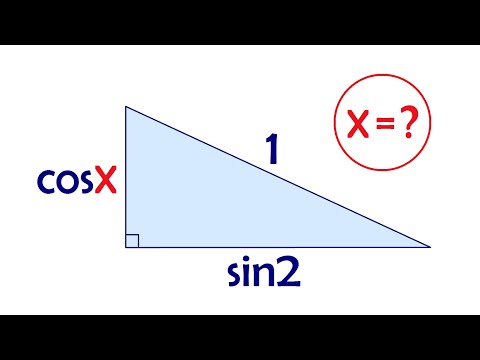
Если кое-что заметить, то решение будет быстрым ★ Найдите площади двух треугольников на рисункеСкачать

Как найти гипотенузу в прямоугольном треугольнике, минуя теорему Пифагора?Скачать

№485. Найдите катет прямоугольного треугольника, лежащий против угла 60°, если гипотенуза равна с.Скачать

Найдите биссектрису прямоугольного треугольника с катетами 3 и 5 ★ Как решать?Скачать

