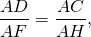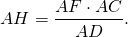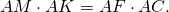На сторонах прямоугольного треугольника ABC, как на диаметрах, построены полуокружности w, w1 и w2. (рис.).
а) Докажите, что площадь треугольника ABC равна сумме площадей двух луночек, ограниченных полуокружностями w и w1 и полуокружностями w и w2.
б) Пусть прямая l касается w1 в точке M, а w2 в точке P. Найдите длину отрезка MP, если известно, что сумма площадей двух луночек равна 49.
а) Пусть AC = b, BC = a, AB = c. И пусть площадь луночки, ограниченной катетом b и дугой окружности ω будет равна D1, а площадь луночки ограниченной катетом a и дугой окружности ω будет равна D2. Тогда площадь треугольника ABC (обозначим SΔ) будет выражена так:
Найдем площадь S1 луночки, которая ограничена полуокружностями ω и ω1.
Аналогично найдем площадь S2 луночки, ограниченной полуокружностями ω и ω2, 
По теореме Пифагора: 
значит, 
(**)
Правые части равенств (*) и (**) совпадают, следовательно, обязаны совпасть и левые части, т. е. 
что и требовалось доказать.
Итак, MP 2 = 49, MP = 7.
Приведём другое решение:
а) Пусть AC = b, BC = a, AB = c. И пусть площадь луночки, ограниченной катетом b и полуокружностью ω, равна D1, катетом a и полуокружностью ω равна D2. Тогда
Правые части равенств (*) и (**) совпадают, следовательно, обязаны совпасть и левые части, т. е. 
что и требовалось доказать.
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Имеется верное доказательство утверждения пункта а и обоснованно получен верный ответ в пункте б. | 3 |
| Получен обоснованный ответ в пункте б. Имеется верное доказательство утверждения пункта а и при обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки. | 2 |
| Имеется верное доказательство утверждения пункта а. При обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки. Содержание Видео:№1125. На сторонах прямоугольного треугольника как на диаметрах построены три полукруга.Скачать  На боковых сторонах трапеции, в которую можно вписать окружность, как на диаметрах построены две окружности. Докажите, что эти окружности имеют одну общую точкуВидео:На сторонах AC и BC треугольника ABC вне треугольника построены квадраты ACDE и BFKC Точка M — сереСкачать 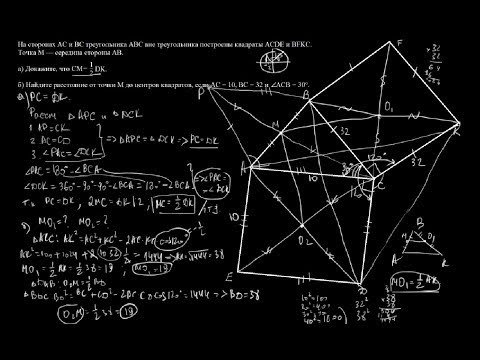 Ваш ответВидео:ЕГЭ Задание 16 Трапеция и две окружностиСкачать 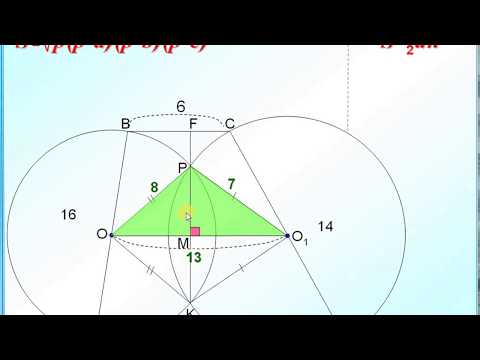 Похожие вопросы
Популярное на сайте: Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах. Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте. Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так. Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью. Видео:ЕГЭ Задание 16 Две окружностиСкачать  На стороне треугольника как на диаметре построена окружностьНа стороне BC остроугольного треугольника ABC (AB≠BC) как на диаметре построена полуокружность, пересекающая высоту AD в точке M, AD=49, MD=42, H — точка пересечения высот треугольника ABC.
AD=49, AD и BF — высоты, AD ∩ BF=H, полуокружность с диаметром BC пересекает AD в точке M, MD=42
Точка F лежит на окружности ( если вписанный угол — прямой, то он опирается на диаметр). Прямоугольные треугольники ADC и AFH подобны по общему острому углу A. Из подобия треугольников следует пропорциональность соответствующих сторон:
По свойству секущих, проведённых из одной точки,
DK=MD=42 (так как диаметр BC перпендикулярен хорде MK, то он проходит через её середину). 🎦 ВидеоДве окружности | Резерв досрока ЕГЭ-2019. Задание 16. Профильный уровень | Борис Трушин |Скачать  Всё про углы в окружности. Геометрия | МатематикаСкачать  ЕГЭ Задание 16 Три окружностиСкачать  Треугольник. На медианах как на диаметрах построены окружности. Задание 16 (34)Скачать  Две окружности на плоскости. Математика. 6 класс.Скачать  ЕГЭ задание 16 Внутреннее касание двух окружностейСкачать  Разбор Задания №16 из Варианта Ларина №291 ЕГЭ-2020.Скачать  ОГЭ Задание 25 Две окружностиСкачать  На катете ML прямоугольного треугольника KLM как на диаметре построена окружностьСкачать  15 задание треугольники огэ по математике / маттаймСкачать  Как просто решить планиметрию. ЕГЭ 2020 математика, 16 номер. Две окружности и трапеция.Скачать  Задача про две вневписанные окружности | ЕГЭ. Задание 16. Математика | Борис Трушин |Скачать  Две окружности в треугольнике. Моё решение.Скачать  7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать  На сторонах прямоугольного треугольника построены полуокружностиСкачать  #математика #огэ #впр На сторонах угла BAC, равного 20°, и на его биссектрисе отложеныСкачать  |
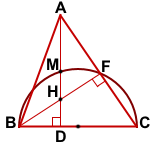Дано: ΔABC,
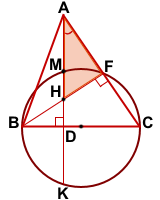Достроим полуокружность до окружности и продлим AD до пересечения с окружностью в точке K.
