На рисунке прямоугольными являются треугольники

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

Зачет по теме: «Треугольники»

1. В треугольнике АВС угол А прямой, при этом другие два угла:

а) один острый, другой может быть прямым или тупым

в) могут быть любыми

г) один острый, другой тупой

2. ∠ 1 = 50°, ∠ ВСК = 134°. Чему равна величина угла А?

а) 84° ; б) 50° ; в) 46° ; г) 40°

3. Если в треугольнике АВС угол А прямой, то:

а) ВС – меньшая его сторона;

б) ВС – большая его сторона;

в) АВ – большая его сторона;

г) АС – большая его сторона.

4. Две стороны треугольника равны 2 см и 4 см. Тогда третья сторона

треугольника может быть равна: а) 6 см; б) 2 см; в) 3 см; г) 1 см.

5. В треугольнике АВС ∠ С = 90°, ∠ В = 60°, СВ = 6 см. Чему равна

сторона АВ? а) 12 см; б) 6 см; в) 3 см; г) 10 см

6. В треугольнике АВС ∠ С = 90°, АВ = 15 см, СВ = 7,5 см. Чему равен ∠ В? а) 90° ; б) 30° ; в) 60° ; г) 45°

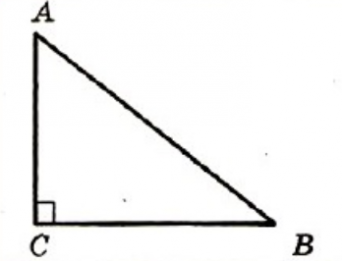
7. Гипотенузой треугольника АВС , изображенного на рисунке является_______

8. В треугольнике АВС сторона АВ – наибольшая. Тогда самым большим углом треугольника будет _______

9. Меньшей стороной треугольника АВС является _________

10. На рисунке прямоугольными треугольниками являются

11. Прямоугольные треугольники, изображенные на рисунке, будут равны

а) по двум катетам;

б) по катету и прилежащему к нему острому углу;

в) по гипотенузе и острому углу;

г) по гипотенузе и катету.

12. Прямоугольные треугольники, изображенные на рисунке, будут равны

а) по двум катетам;

б) по катету и прилежащему к нему острому углу;

в) по гипотенузе и острому углу;

г) по гипотенузе и катету.

13. Прямоугольные треугольники, изображенные на рисунке, будут равны

а) по двум катетам;

б) по катету и прилежащему к нему острому углу;

в) по гипотенузе и острому углу;

г) по гипотенузе и катету.

14. На рисунке к прямой a

а) АС – перпендикуляр, ВС – наклонная;

б) АВ – наклонная, ВС – перпендикуляр;

в) АС – наклонная, АВ – перпендикуляр;

г) АС – перпендикуляр, АВ – наклонная

15 . Длина катета ВС треугольника АВС будет равна _______

16. В прямоугольном треугольнике АВС ∠ А = 90°, АВ = 4 см, АС = 6 см. Расстояние от точки С до прямой АВ будет равно ______

17. В треугольнике АВС больший острый угол треугольника будет равен________

18. Найдите угол при вершине равнобедренного треугольника, если угол при основании равен 40°.

19. В треугольнике АВС ∠ В = 80°, ∠ С = 60°. Укажите наименьшую сторону этого треугольника.

20. Используя данные, отмеченные на рисунке, определите, какой из треугольников является равнобедренным и укажите его основание.

21. Стороны прямоугольного треугольника равны 8, 15 и 17. Укажите длину гипотенузы.

22. Используя данные, указанные на рисунке, найдите угол а

23. Если в прямоугольном треугольнике один из углов равен 54°, тогда другой острый угол будет равен ________

24. Точка К лежит внутри угла ВМС и находится на одинаковом расстоянии от сторон угла, ∠ ВМК = 54° . Найдите ∠ ВМС. Ответ объяснить.

25. РК – серединный перпендикуляр к отрезку NL , PL = 4, NL = 7. Найдите периметр треугольника PNL . Ответ объяснить.

Зачет по теме: «Треугольники»

1. В треугольнике АВС угол В тупой, при этом другие два угла:

а) только острые

б) острый и прямой

в) острый и тупой

2. ∠ 1 = 55°, ∠ А = 76°. Чему равен угол ВСК?

а) 135° ; б) 104° ; в) 131° ; г) 125°

3. Если в треугольнике АВС угол В тупой, то:

а) АС – меньшая его сторона;

б) ВС – большая его сторона;

в) АВ – меньшая его сторона;

г) АС – большая его сторона.

4. Две стороны треугольника равны 5 см и 4 см. Тогда третья сторона

треугольника может быть равна: а) 9 см; б) 4 см; в) 1 см; г) 12 см.

5. В треугольнике АВС ∠ С = 90°, ∠ В = 60°, АВ = 10 см. Чему равна

сторона ВС? а) 20 см; б) 10 см; в) 6 см; г) 5 см

6. В треугольнике АВС ∠ С = 90°, АВ = 18 см, АС = 9 см. Чему равен ∠ А?

а) 60° ; б) 90° ; в) 30° ; г) 45°

7. Катетами треугольника АВС , изображенного на рисунке является: ___

8. В треугольнике АВС ∠ А – самый большой. Тогда большей стороной

треугольника АВС является __________

9. Большей стороной треугольника MNK является _________

10. На рисунке тупоугольными треугольниками являются треугольники____

11. Прямоугольные треугольники, изображенные на рисунке, будут равны

а) по двум катетам;

б) по катету и прилежащему к нему острому углу;

в) по гипотенузе и острому углу;

г) по гипотенузе и катету.

12. Прямоугольные треугольники, изображенные на рисунке, будут равны

а) по двум катетам;

б) по катету и прилежащему к нему острому углу;

в) по гипотенузе и острому углу;

г) по гипотенузе и катету.

13. Прямоугольные треугольники, изображенные на рисунке, будут равны

а) по двум катетам;

б) по катету и прилежащему к нему острому углу;

в) по гипотенузе и острому углу;

г) по гипотенузе и катету.

а) НК – наклонная, ВК – перпендикуляр;

б) НВ – перпендикуляр, ВК – наклонная;

в) НК – перпендикуляр, ВК – наклонная;

г) НК – перпендикуляр, ВН – наклонная;

15. Длина гипотенузы треугольника АВС будет равна _______

16. В прямоугольном треугольнике АВС ∠ А = 90°, АВ = 6 см, АС = 10 см. Расстояние от точки В до прямой АС будет равно ______

17. В треугольнике MNK острые углы треугольника будут равны _____

18. Найдите угол при основании равнобедренного треугольника, если угол при вершине равен 40°.

19 . В треугольнике АВС ∠ А = 60°, ∠ С = 50°. Укажите наибольшую сторону этого треугольника.

20. Используя данные, отмеченные на рисунке, определите, какой из треугольников является равнобедренным и укажите его основание.

21. Стороны прямоугольного треугольника равны 12, 16 и 20. Укажите длину гипотенузы.

22. Используя данные, указанные на рисунке, найдите угол а

23. Если в прямоугольном треугольнике один из углов равен 32°, тогда другой острый угол будет равен ________

24. Точка М лежит внутри угла АОС и находится на одинаковом расстоянии от сторон угла, ∠ АОС = 82° . Найдите ∠ МОС. Ответ объяснить.

25. РН – серединный перпендикуляр к отрезку MN , MH = 6, MN = 8. Найдите периметр треугольника MNH . Ответ объяснить.

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 958 человек из 79 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 310 человек из 70 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 679 человек из 74 регионов

Ищем педагогов в команду «Инфоурок»

Видео:Свойства прямоугольного треугольника. 7 класс.Скачать

Дистанционные курсы для педагогов

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 553 540 материалов в базе

Материал подходит для УМК

«Геометрия», Бутузов В.Ф., Кадомцев С.Б., Прасолов В.В. / Под ред. Садовничего В.А.

Другие материалы

• 24.03.2018
• 4367
• 111

• 24.03.2018
• 1028
• 5

• 24.03.2018
• 1820
• 10

• 24.03.2018
• 5380
• 275

• 24.03.2018
• 2312
• 8

• 24.03.2018
• 5039
• 2

• 24.03.2018
• 1521
• 6

• 24.03.2018
• 3482
• 0

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 24.03.2018 2951
• DOCX 544.8 кбайт
• 5 скачиваний
• Рейтинг: 2 из 5
• Оцените материал:

Настоящий материал опубликован пользователем Шрам Светлана Михайловна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 5 лет и 4 месяца
• Подписчики: 0
• Всего просмотров: 29315
• Всего материалов: 8

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Все про прямоугольный треугольник. Решаем задачи | Математика | TutorOnlineСкачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

У 76% российских учителей оклад ниже МРОТ

Время чтения: 2 минуты

В «Единой России» предложили ввести раздел безопасности детей в интернете в курс ОБЖ

Время чтения: 3 минуты

Полный перевод школ на дистанционное обучение не планируется

Время чтения: 1 минута

Петербургская учительница уволилась после чтения на уроке Введенского и Хармса

Время чтения: 3 минуты

В Египте нашли древние школьные «тетрадки»

Время чтения: 1 минута

Онлайн-семинар о развитии управляющих функций мозга ребенка

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:Геометрия 7 класс (Урок№25 - Прямоугольные треугольники.)Скачать

Прямоугольный треугольник. Теорема Пифагора.

теория по математике 📈 планиметрия

Если в треугольнике есть угол, равный 90 градусов, то такой треугольник называется прямоугольным. Стороны прямоугольного треугольника называются – катеты и гипотенуза. Катеты – это стороны, образующие прямой угол. Гипотенуза – сторона, которая располагается напротив прямого угла.

На рисунке треугольник АВС – прямоугольный, угол С равен 90º, стороны АС и ВС – катеты, а сторона АВ – гипотенуза.

Видео:Профильный ЕГЭ 2024. Задача 1. Прямоугольный треугольник. 10 классСкачать

Свойства прямоугольного треугольника

• В прямоугольном треугольнике гипотенуза является наибольшей стороной.
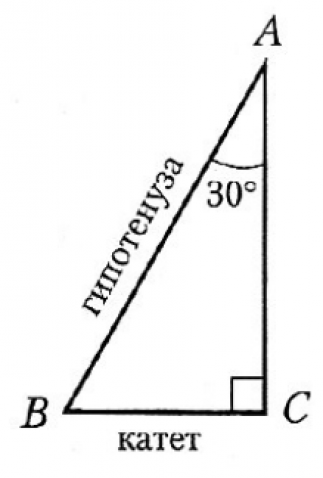
• В прямоугольном треугольнике катет, лежащий напротив угла 30 0 , равен половине гипотенузы. И обратно, если катет равен половине гипотенузы, то угол, лежащий напротив этого катета, равен 30 0 .

Например, пусть угол А=30 0 , а гипотенуза АВ=28 см, то катет ВС будет равен 14 см, так как лежит напротив угла А=30 0 . Или, например, если катет ВС=6 см, а гипотенуза АВ равна 12 см, то угол А (лежащий напротив катета ВС), равен 30 0 .

• Сумма острых углов прямоугольного треугольника равна всегда 90 градусов.
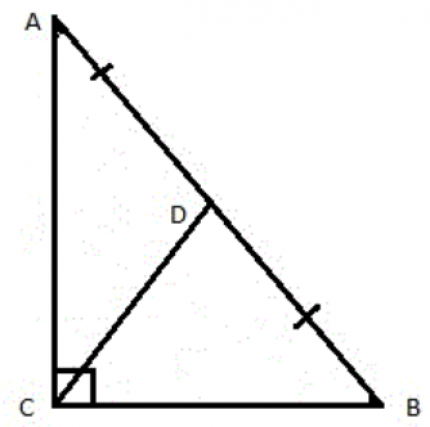
• Медиана, проведенная к гипотенузе, равна её половине.

На рисунке изображен прямоугольный треугольник АВС, где CD – медиана, проведенная к гипотенузе. По свойству – медиана CD=0,5АВ, то есть AD=DB=CD.

Видео:7 класс, 32 урок, Остроугольный, прямоугольный и тупоугольный треугольникиСкачать

Признаки равенства прямоугольных треугольников

Существует 4 признака равенства прямоугольных треугольников:

1. Если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны.
2. Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и острому углу другого прямоугольного треугольника, то такие треугольники равны.
3. Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны.
4. Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны.

Чтобы быстрее запомнить данные признаки, можно использовать их краткую трактовку:

1. по катетам;
2. по катету и прилежащему острому углу;
3. по гипотенузе и острому углу;
4. по гипотенузе и катету.

Видео:По силам каждому ★ Найдите стороны треугольника на рисункеСкачать

Теорема Пифагора

Древнегреческий философ, ученый, математик – Пифагор Самосский вывел теорему, которая до сих применима для решения задач. Теорема названа в честь него – «теорема Пифагора».

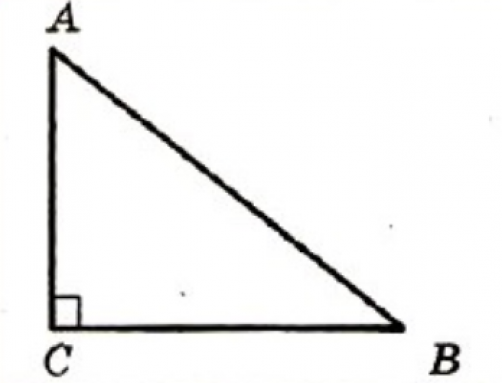
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

На рисунке в прямоугольном треугольнике АВ 2 =АС 2 +ВС 2

Например, если в данном треугольнике катеты равны 9 и 12 см, то можно найти длину гипотенузы, используя теорему: АВ 2 =9 2 +12 2 =81+144=225=15 2 , значит АВ=15 см.

Египетский треугольник

Треугольник со сторонами 3, 4 и 5 см называют Египетским треугольником.

Пифагоровы тройки

Тройки чисел, которые удовлетворяют теореме Пифагора, называют Пифагоровы тройки, а сами числа – Пифагоровы числа. Например, такими являются числа 16, 12 и 20 – это числа, которые при подстановке в формулу теоремы, дают нам верное равенство: 16 2 +12 2 =20 2 , 256+144=400, 400=400.

Видео:Решение прямоугольных треугольников. Практическая часть. 8 класс.Скачать

Виды треугольников (по сторонам)

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

На данном уроке учащимся предоставляется возможность обобщить знания о названиях и изученных свойствах геометрических фигур, познакомиться с основными свойствами треугольника, узнать виды треугольников по величине угла, по числу равных сторон, потренироваться в распознавании названных видов.

🎦 Видео

Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

7 класс, 36 урок, Признаки равенства прямоугольных треугольниковСкачать

Треугольники: остро-, тупо- и прямоугольныеСкачать

8 класс, 26 урок, Пропорциональные отрезки в прямоугольном треугольникеСкачать

Всё про прямоугольный треугольник за 15 минут | Осторожно, спойлер! | Борис Трушин !Скачать

Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Задача по геометрии на прямоугольный треугольник и теорему Пифагора из реального ОГЭ по математикеСкачать

Свойства прямоугольного треугольника. Практическая часть. 7 класс.Скачать

Математика | Соотношения между сторонами и углами в прямоугольном треугольнике.Скачать

Виды треугольниковСкачать

Построение высоты в тупоугольном и прямоугольном треугольниках. 7 класс.Скачать

Решение прямоугольных треугольников | Алгебра 10 класс #16 | ИнфоурокСкачать

Геометрия. 7 класс. Прямоугольные треугольники.Скачать