На продолжении диаметра ав окружности

Видео:№144. Отрезки АВ и CD — диаметры окружности. Докажите, что: а) хорды BD и АС равны; б) хорды AD и ВССкачать

Ваш ответ

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

решение вопроса

Видео:На окружности по разные стороны от диаметра AB ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Похожие вопросы

• Все категории
• экономические 43,277
• гуманитарные 33,618
• юридические 17,900
• школьный раздел 606,857
• разное 16,824

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:№145. Отрезок МК — диаметр окружности с центром О, а МР и РК — равные хорды этой окружностиСкачать

На продолжении диаметра АВ за точку В взята точка С?

Математика | 10 — 11 классы

На продолжении диаметра АВ за точку В взята точка С.

СР – касательная к окружности (точка Р – точка касания), а угол АРС равен 110 градусов .

Найти угловую величину дуги ВР.

Пусть точка О — центр окружности.

Видео:Радиус и диаметрСкачать

Из точки а проведены две касательные к окружности с центром в точке О?

Из точки а проведены две касательные к окружности с центром в точке О.

Из точки а проведены две касательные к окружности с центром в точке О.

Найдите радиус окружности, если угол между касательными равен 60 градусов, а расстояние от точки А до точки О равно 8.

По подробнее пожалуйста.

Видео:Геометрия Две окружности имеют общий центр O (см. рис.). В одной из окружностей проведен диаметр ABСкачать

Отрезок прямой AB — хорда окружности с центром в точке О?

Отрезок прямой AB — хорда окружности с центром в точке О.

Угол AOB равен 146 градусам.

Найдите величину угла между прямой Ab и касательной к окружности, проходящей через точку A.

Видео:№148. На прямой даны две точки А и В. На продолжении луча ВА отложите отрезок ВС так, чтобы ВС= 2АВ.Скачать

Диаметр шара равен 8 см?

Диаметр шара равен 8 см.

Точка А принадлежит касательной плоскости к шару и находится на расстоянии 3 см от точки касания шара к плоскости.

Найти расстояние от точки А до центра шара.

Видео:Окружность, диаметр, хорда геометрия 7 классСкачать

Отрезок прямой АВ — хорда окружности с центром в точке О?

Отрезок прямой АВ — хорда окружности с центром в точке О.

Угол АОВ равен 146″(градусов).

Найдите величину угла между прямой и касательной к окружности, проходящей через точку А.

Видео:№146. Отрезки АВ и CD — диаметры окружности с центром О. Найдите периметр треугольника AOD, еслиСкачать

Угол между касательной и хордой проведенной из точки касания равен 37?

Угол между касательной и хордой проведенной из точки касания равен 37.

Найдите величину дуги высекаемой на окружности этой хордой.

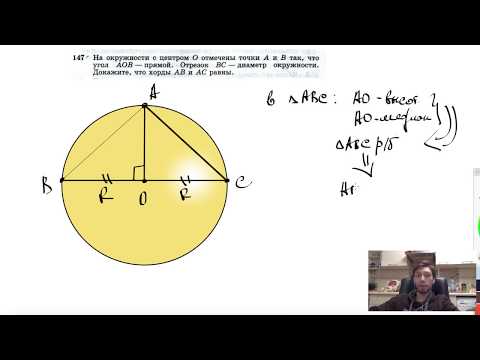
Видео:№147. На окружности с центром О отмечены точки А и В так, что угол АОВ — прямой. Отрезок ВССкачать

Найдите уравнение кривой, проходящей через точку М ( — 1 ; 3), если угловой коэффициент касательной в любой точке кривой равен утроенному квадрату абсциссы точки касания?

Найдите уравнение кривой, проходящей через точку М ( — 1 ; 3), если угловой коэффициент касательной в любой точке кривой равен утроенному квадрату абсциссы точки касания.

Видео:Геометрия 8 класс (Урок№28 - Свойства хорд окружности.)Скачать

К окружности с центром в точке о из точки а проведены две касательные, угол между которыми равен 120 градусов найдите длины отрезков касательных если она = 24см?

К окружности с центром в точке о из точки а проведены две касательные, угол между которыми равен 120 градусов найдите длины отрезков касательных если она = 24см.

Видео:Геометрия В окружности проведены диаметр AC и хорда AB равная радиусу окружности Найдите углыСкачать

Касательные CA и CB к окружности образуют угол ACB, равный 820 ?

Касательные CA и CB к окружности образуют угол ACB, равный 820 .

Найдите величину меньшей дуги AB, стягиваемой точками касания.

Ответ дайте в градусах.

Видео:Разбор планиметрии (№16) из Досрочного ЕГЭ 2023Скачать

Прямая касается окружности в точке К, Точка О — центр окружности хорда км образует с касательной угол равный 19 грдусов?

Прямая касается окружности в точке К, Точка О — центр окружности хорда км образует с касательной угол равный 19 грдусов.

Найти величину угла омк ответ дайте в градусах.

Видео:№662. Хорды АВ и CD окружности пересекаются в точке Е. Найдите угол ВЕС, если ∪AD=54°, ∪BC= 70°.Скачать

Угол межу диаметром ав и хордой ас окружности равен 45 градусам?

Угол межу диаметром ав и хордой ас окружности равен 45 градусам.

Через точку с проведена касательная к окружности которая пересекает прямую ав в точке D.

Определите вид треугольника ACD.

На этой странице сайта, в категории Математика размещен ответ на вопрос На продолжении диаметра АВ за точку В взята точка С?. По уровню сложности вопрос рассчитан на учащихся 10 — 11 классов. Чтобы получить дополнительную информацию по интересующей теме, воспользуйтесь автоматическим поиском в этой же категории, чтобы ознакомиться с ответами на похожие вопросы. В верхней части страницы расположена кнопка, с помощью которой можно сформулировать новый вопрос, который наиболее полно отвечает критериям поиска. Удобный интерфейс позволяет обсудить интересующую тему с посетителями в комментариях.

Видео:ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать

Презентация задач по планиметрии второй части профильного ЕГЭ (С4)

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Видео:Отрезки AC и BD – диаметры окружности с центром O ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

Решение задач С4

Содержание Задача 1 Задача 2 Задача 3 Задача 4 Задача 5 Задача 6 Задача 7 Задача 8 Задача 9 Задача 10 Задача 11 Задача 12 (теорема) Задача 13 Задача 14 Задача15

1. В прямоугольном треугольнике ABC гипотенуза АВ равна c и ∠ABC=α.Найдите все медианы в этом треугольнике. Р е ш е н и е. Поскольку медиана прямоугольного треугольника, проведённая из вершины прямого угла, равна половине гипотенузы, медиана CM равна . Пусть K– середина BC.Тогда CK= BC= AB*cosα= *c*cos α.По теореме Пифагора из прямоугольного треугольника ACK находим, что AK= = = = = = = Аналогично находим медиану BN.

2. В треугольнике ABC проведена медиана BM. Известно, что . Найдите отношение . Р е ш е н и е. На продолжении медианы BM за точку M отложим отрезок MD, равный BM. Диагонали AC и BD четырёхугольника ABCD делятся точкой пересечения M пополам, значит, ABCD – параллелограмм. Поэтому AB=BC и ∠ADB= ∠CBM. По теореме синусов из треугольника ABD находим, что Следовательно,

3. В выпуклом четырёхугольнике ABCD отрезки, соединяющие середины противоположных сторон, пересекаются под углом 60˚,а их длины относятся как 1:3. Чему равна меньшая диагональ четырёхугольника ABCD, если большая равна . Р е ш е н и е. Середины сторон любого четырёхугольника являются вершинами параллелограмма, стороны которого параллельны диагоналям четырёхугольника и соответственно равны их половинам. Обозначим через x и 3x половины диагоналей параллелограмма. Поскольку угол между ними равен 60˚, то по теореме косинусов квадраты сторон параллелограмма равны x²+9x²-3x²=7x² , x²+9x²+3x²=13x² Поскольку большая диагональ четырёхугольника равна , большая сторона параллелограмма равна , т. е. 13х²= , откуда x= . Тогда меньшая сторона параллелограмма равна . Следовательно, меньшая диагональ данного четырёхугольника равна

4. Найдите площадь трапеции с основаниями 18 и 13 и боковыми сторонами З и 4. Р е ш е н и е. Через вершину С меньшего основания ВС трапеции АВСD (ВC=13, АD=18, АВ=4, СD=3) проведём прямую, параллельную боковой стороне АВ, до пересечения с основанием АD в точке К. Тогда СК=АВ=4, DK=АD — АК=АD — ВС=18 — 13=5, СD=З. Треугольник КСD прямоугольный, так как КD²=СD²+СК². Его высота, опущенная на гипотенузу, равна . Следовательно, SABCD

5. Две стороны треугольника равны З и 6, а угол между ними ра 60°. Найдите биссектрису треугольника, проведённую из верши этого угла. Решение. Пусть АD — биссектриса треугольника АВС, в котором АВ =6, АС =3, ∠ВАС=60°. Первый способ. Обозначим AD=x. Тогда SABC= SABC=SABC+SACD= = Из уравнения находим, что x=2 Второй способ. Заметим, что треугольник АВС прямоугольный. Тогда треугольник ACD также прямоугольный, причём САD =30°. Следовательно, AD=AC:cos∠CAD=3:cos30°=2

6. Отношение отрезков Точки M и N – середины сторон соответственно BC и CD параллелограмма ABCD. Отрезки AM и BN пересекаются в точке O. Найдите отношение .

Решение: 1.Пусть продолжения BN и AD пересекаются в точке E. И пусть BM=MC=a.Тогда BC=AD=2a. 2. DNE= CNB по двум углам и стороне между ними а) CN=ND (по условию) б) CNB= DNE (как вертикальные) в) EDN= BCN (как соответственные) => DE=BC=2a. 3. AE=AD+DE=4a. 4. BOM

EOA (по 3 углам) 5. = = = B a M a C O N A 2a D

7. Отношение площадей. В треугольнике ABC медиана AD и биссектриса BE перпендикулярны и пересекаются в точке F. Известно, что площадь треугольника DEF равна 5. Найдите площадь треугольника ABC.

Решение: 1) ABD равнобедренный, так как биссектриса BF — высота => AF=FD 2) AFE= DFE (по углу и двум сторонам) => = = 5 3) BC = 2BD = 2BA, тогда = = 2 (по св-ву биссектрисы) 4) = 2 = 4 =20 5) = + = 10 + 20 = 30 6) = = 1 => = = 30 7) = 60

8. Касательная к окружности Из точки M, лежащей вне окружности с центром O и радиусом R, проведены касательные MA и MB (A и B – точки касания). Прямые OA и MB пересекаются в точке C. Найдите OC, если известно, что отрезок OM делит окружность пополам.

Решение: 1) Пусть K – точка пересечения окружности с отрезком OM. Тогда OM = 2OK = 2R 2) В OAM ( MAO= ) катет OA меньше гипотенузы в 2 раза OM => AMO = 3) AMC= (т.к. MO – биссектриса AMC) 4) Из MAC ( MAC= ) : ACM = => COM – равнобедренный => OM= MO= 2R ∆ ∆ ∆

9. Касающиеся окружности Окружности с центрами и касаются внешним образом в точке C. Прямая касается этих окружностей в различных точках A и B соответственно. Найдите угол A B, если известно, что tg ABC = .

Решение: 1) Проведём общую касательную из точки C 2) Пусть она пересекает прямую AB в точке M => MA=MC=MB => ABC = 90 3) Опустим перпендикуляр H на её хорду CB, тогда CH=HB 4) т.к. tg ABC = = , тогда AC= BC = BH 5) B H = 90 — BH= ABC => B H = ABC (по катету и острому углу) 6) B =AB => A B= BA= 45

10. Задача. На катетах прямоугольного треугольника, как на диаметрах, построены окружности. Найдите их общую хорду, если катеты равны 3 и 4. Решение. Пусть СD – общая хорда окружностей, построенных на катетах АС = 3 и ВС = 4 прямоугольного треугольника АВС как на диаметрах. (как вписанные углы, опирающиеся на диаметр). Значит, точка D лежит на гипотенузе АВ, а СВ – высота прямоугольного треугольника АВС, проведённая из вершины прямого угла. Тогда по теореме Пифагора: SABC= ½*AC*BC и SABC= ½*AB*CD Получаем ½*AC*BC= ½*AB*CD, откуда выражаем CD. Ответ: 2,4 А B C D

11. Задача. Найдите радиусы вписанной и описанной окружности треугольника со сторонами 13, 13, 24 и расстояние между центрами этих окружностей. Решение. Пусть CD – высота равнобедренного треугольника ABC со сторонами AC=BC=13 и AB=24, О – центр его описанной окружности радиуса R, Q – центр вписанной окружности радиуса r. Из прямоугольного треугольника ACD находим, что По теореме синусов:

Радиус окружности, вписанной в треугольник, равен площади треугольника, делённой на его полупериметр, поэтому Заметим, что поэтому точки O и Q лежат по разные стороны от AB. Следовательно OQ=OC – CQ=OC – (CD – QD)= R – (CD – r)=16,9 – (5 – 2,4)=14,3 Ответ:16,9; 2,4; 14,3.

Пропорциональные отрезки в окружности Теорема. Произведения отрезков пересекающихся хорд окружности равны, т.е. если хорды AB и CD окружности пересекаются в точке M, то AM*MB=CM*MD. Пример 1. Из точки А, лежащей вне окружности, проведены к окружности касательная и секущая. Расстояние от точки А до точки касания равно 16, а до одной из точек пересечения секущей с окружностью равно 32. Найдите радиус окружности, если расстояние от неё до центра секущей равно 5. Решение. Пусть секущая пересекает окружность в точках B и C, а М – точка касания. Тогда АМ=16, АС=32, АВ+ВС=32. По теореме о касательной и секущей AM=AC*AB, или 16²=32(32-ВС). Отсюда находим, что ВС=24. Пусть К – проекция центра О данной окружности на хорду ВС. Радиус окружности находим по теореме Пифагора из прямоугольного треугольника ОКВ: Ответ: 13

Рассмотрим ещё один пример. Пример 2. Докажите, что прямая, проходящая через точки пересечения двух окружностей, делит пополам общую касательную к ним Доказательство. Пусть А и В – точки пересечения двух окружностей, МN – общая касательная (М и N точки касания), К – точка пересечения прямых АВ и MN (А между К и В). Тогда МК²=КВ*КА и NK²=KB*KA. Следовательно МК=NK, что и требовалось доказать.

12. Задача. На продолжении диаметра АВ окружности отложен отрезок ВС, равный диаметру. Прямая, проходящая через точку С, касается окружности в точке М. Найдите площадь треугольника АСМ, если радиус окружности равен R. Решение. Пусть О – центр окружности. Тогда ОМ⏊СМ. В прямоугольном треугольнике ОМС известно, что ОМ=R и ОС=ОВ+ВС=R+2R=3R. Тогда Следовательно, Ответ:

13. Задача. Окружность S1 проходит через центр окружности S2 и пересекает её в точках A и B. Хорда AC окружности S1 касается окружности S2 в точке А и делит первую окружность на дуги, градусные меры которых относятся как 5:7. Найдите градусные меры дуг, на которые окружность S2 делится окружностью S1. Решение. Пусть О1 и О2 – центры окружностей S1 и S2 соответственно. Тогда Поскольку ∠О₁AC=90ᵒ (радиус, проведённый в точку касания, перпендикулярен касательной), отрезок О₂С – диаметр окружности S₁, поэтому Тогда градусная мера дуги окружности S₂, заключённой между сторонами угла AO₂C, равна 75ᵒ, а градусная мера дуги AB окружности S₂, содержащейся внутри окружности S₁, равна 150ᵒ. Следовательно, дополнительная к ней дуга окружности S₂ равна 360ᵒ-150ᵒ=210ᵒ Ответ: 150ᵒ, 210ᵒ

14. Задача. На стороне АВ треугольника АВС отмечена точка D, причём ∠BCD=∠BAC. Известно, что ВС=a, AC=b, AB=c. Найдите CD. Решение. Треугольники CBD и АВС подобны по двум углам, т.к. ∠BCD=∠BAC по условию, а угол при вершине В – общий. Значит, соответствующее стороны этих треугольников пропорциональны, т.е. Следовательно, Ответ:

15. Задача. Углы при вершинах A и С треугольника АВС равны 45ᵒ и 60ᵒ соответственно; АМ, BN иCK – высоты треугольника. Найдите отношение MN к KN Решение. Из прямоугольных треугольников BNC и АМС находим что CN=BCcos60ᵒ=0,5BC, CM=AC*cos60ᵒ=0,5AC, поэтому Значит, треугольник CMN подобен треугольнику САВ по двум сторонам и углу между ними (угол С – общий), причём коэффициент подобия равен Следовательно, MN=0,5AB. Аналогично получим, что треугольник AKN подобен треугольнику ACB, причём коэффициент подобия равен Значит, По теореме синусов: Следовательно: Ответ:

💥 Видео

Как Эратосфен измерил диаметр Земли?Скачать

№662 (исправлено) Хорды АВ и CD окружности пересекаются в точке Е. Найдите угол ВЕС, если ∪AD=54°Скачать

🔴 В окружности с центром O отрезки AC и BD ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 15 | ШКОЛА ПИФАГОРАСкачать

Разбор планиметрии №16 Досрочный ЕГЭ 2023Скачать