- Ваш ответ
- решение вопроса
- Похожие вопросы
- На окружности с центром о и диаметром ав равным 4
- 1) На окружности с центром O и диаметром AB, равным 4, взята точка M, расположенная ближе к точке A, чем к точке B?
- Из точки А проведены две касательные к окружности с центром в точке О?
- Из точки А проведены две касательные к окружности с центром в точке О?
- Из точки А проведены две касательные к окружности с центром в точке О?
- На окружности с центром О и диаметром АВ , равным 4, взята точка М, ближе к точке А, чем к точке В?
- Из точки А проведены две касательные к окружности с центром в точке О?
- Отрезок AB является диаметром окружности с центром в точке О?
- Докажите , что отрезки касательных к окружности , проведённые из одной точки, равны и составляют равные углы с прямой , проходящей через эту точку и центр окружности?
- Из точки А проведены две касательные к окружности с центром в точке О?
- Из точки А проведены две касательные к окружности с центром в точке О?
- Из точки А проведены две касательные к окружности с центром в точке О?
- 📸 Видео
Видео:2175 AC и BD диаметры окружности с центром О угол acb равен 35 Найдите угол aodСкачать

Ваш ответ
Видео:2023 На окружности с центром в точке О отмечены точки А и Б так что угол аоб равен 45Скачать

решение вопроса
Видео:№145. Отрезок МК — диаметр окружности с центром О, а МР и РК — равные хорды этой окружностиСкачать

Похожие вопросы
- Все категории
- экономические 43,283
- гуманитарные 33,619
- юридические 17,900
- школьный раздел 607,073
- разное 16,829
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Видео:Радиус и диаметрСкачать

На окружности с центром о и диаметром ав равным 4
На окружности с центром O и диаметром MN, равным 34, взята точка K на расстоянии 15 от этого диаметра. Хорда KE пересекает радиус OM в точке F под углом, равным
а) Докажите, что KF : FE = 125 : 29.
б) Найдите площадь треугольника KEN.
а) Пусть KP — высота треугольника MKN. Из прямоугольных треугольников KOP и KPF находим, что
Отрезок PF длиннее радиуса окружности. Значит, точки F и P лежат по разные стороны от точки O. Тогда
По теореме о произведении отрезков пересекающихся хорд получаем, что
откуда находим, что
б) Для нахождения площади треугольника KEN воспользуемся формулой
Из треугольника KOP находим, что
Из треугольника EFN получаем, что
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б) | 3 |
| Получен обоснованный ответ в пункте б) имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | 2 |
| Имеется верное доказательство утверждения пункта а) при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, Видео:На окружности с центром O отмечены точки A и B так ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать  1) На окружности с центром O и диаметром AB, равным 4, взята точка M, расположенная ближе к точке A, чем к точке B?Геометрия | 5 — 9 классы 1) На окружности с центром O и диаметром AB, равным 4, взята точка M, расположенная ближе к точке A, чем к точке B. Через точку M проведена касательная к окружности, а через точки A и B — лучи, перпендикулярные к AB и пересекающие касательную в точках D и C соответственно, уголDCB = 60⁰. А) Найдите углы OCB, ADC, ODC. Б) Найдите отрезки AD и CB. В) Найдите площадь четырехугольника ABCD. Г) Найдите углы четырехугольника MOBC. Д) Докажите, что треугольники AOD и COB подобны. Е) Докажите, что расстояние от точки O до середины отрезка DC равно 0, 5(MD + BC). Ж) Выразите OM через OD и OC (над OM, OD и OC стрелочки). Угол ОСВ = 15 градусов, потому что ОС — биссектриса угла МСВ. (биссектриса ПО ОПРЕДЕЛЕНИЮ равноудалена от сторон угла. ) угол ADC = 180 — 30 = 150 градусов, угол ОDC = 150 / 2 = 75 градусов. (ОD тоже биссектриса, угла ADC). Отсюда сразу же следует, что угол DOC прямой — в треугольнике DOC сумма двух других углов равна 75 + 15 = 90. Кроме того, ОМ — высота DOC, а высота прямоугольного треугольника делит его на два, подобных ему. Это означает DM / OM = OM / MC, или DM * MC = MO ^ 2 = 4. DC найти тоже легче простого — если провести в DCAB перпендикуляр из D на ВС (пусть это DK, ясно, что DK = AB = 4), то получится прямоугольный треугольник CDK с углом С 30 градусов, то есть DC = 2 * DK = 8. Получилось DM * МС = 4 ; DM + MC = 8 ; Отсюда (DM + MC) ^ 2 — 4 * DM * MC = 48 ; (DM — MC) ^ 2 = 48 ; MC — DM = 4 * √3 (по условию МС> ; DM) ; 2 * MC = 8 + 4 * √3 ; MC = 4 + √3 ; DM = 4 — √3 ; АD = DM (касательные из одной точки) и аналогично CВ = СМ. Средняя линяя трапеции ADCB равна (AD + CB) / 2 = DC / 2 = 4, высота равна АВ = 8 площадь 16. Угол МОВ равен 360 — 2 * 90 — 30 = 150. Подобие треугольников DMO и CMO я уже доказал, а треугольник AOD = DMO, и СОВ = MOC (докажите, это вообще элементарно, там есть общие стороны и равные углы). Е) уже доказано (перечитайте : )) и последнее — вектора OD, OM, ОС, и еще нужен DM. Ясно, что длина DM = 4 — √3, поэтому вектор DM = DC * (4 — √3) / 8 ; ОМ = ОD + DM (вектора! ) = OD + DC * (4 — √3) / 8 = OD + (OC — OD) * (4 — √3) / 8 = OC * (4 — √3) / 8 + OD * * (4 + √3) / 8 = OC * (4 — √3) / 8 + OD * (4 + √3) / 8. Видео:№638. Прямая АВ касается окружности с центром О радиуса r в точке В. Найдите АВСкачать  Из точки А проведены две касательные к окружности с центром в точке О?Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 8. Видео:№147. На окружности с центром О отмечены точки А и В так, что угол АОВ — прямой. Отрезок ВССкачать 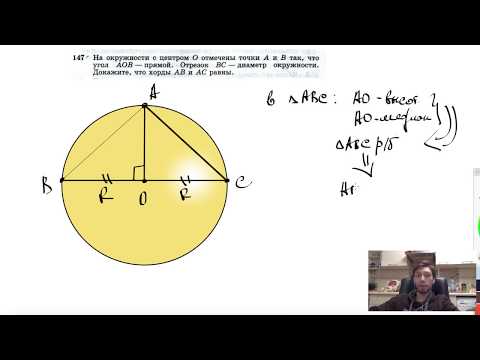 Из точки А проведены две касательные к окружности с центром в точке О?Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности. Если угол между касательными равен 60, а расстояние от точки А до точки О равно 8. Видео:№144. Отрезки АВ и CD — диаметры окружности. Докажите, что: а) хорды BD и АС равны; б) хорды AD и ВССкачать  Из точки А проведены две касательные к окружности с центром в точке О?Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 8. Видео:🔴 В окружности с центром O отрезки AC и BD ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 15 | ШКОЛА ПИФАГОРАСкачать  На окружности с центром О и диаметром АВ , равным 4, взята точка М, ближе к точке А, чем к точке В?На окружности с центром О и диаметром АВ , равным 4, взята точка М, ближе к точке А, чем к точке В. Через точку М проведена касательная к окружности, а через точки А и В — лучи, перпендикулярные к АВ и пересекающие касательную в точках Д и С соответственно, угол ДСВ = 60 градусов. А) найдите углы ОСВ, АДС, ОДС. Б) найдите отрезки АД и СВ в) найдите S четырёхугольника АВСД г) найдите углы четырёхугольника МОВС д) докажите, что треугольники АОД и СОВ подобны. Видео:№146. Отрезки АВ и CD — диаметры окружности с центром О. Найдите периметр треугольника AOD, еслиСкачать  Из точки А проведены две касательные к окружности с центром в точке О?Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 6. Видео:Отрезки AC и BD – диаметры окружности с центром O ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать  Отрезок AB является диаметром окружности с центром в точке О?Отрезок AB является диаметром окружности с центром в точке О. В точках А и В проведены касательные к окружности. Через центр окружности проведена прямая, которая пересекает касательные в точках C и D. Докажите, что длины отрезков OC и OD равны. Заранее огромное спасибо♥. Видео:На окружности по разные стороны от диаметра AB ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать  Докажите , что отрезки касательных к окружности , проведённые из одной точки, равны и составляют равные углы с прямой , проходящей через эту точку и центр окружности?Докажите , что отрезки касательных к окружности , проведённые из одной точки, равны и составляют равные углы с прямой , проходящей через эту точку и центр окружности. Видео:2035 В окружности с центром в точке О отрезки AC и BD диаметрыСкачать  Из точки А проведены две касательные к окружности с центром в точке О?Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60гр, а расстояние от точки А до точки О равно 6. Видео:Как найти центр круга с помощью подручных средств? ЛЕГКО.Скачать  Из точки А проведены две касательные к окружности с центром в точке О?Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности если угол между касательными равен 60°, а расстояние от точки А до точки О равно 8. Видео:2017 на окружности по разные стороны от диаметра AB взяты Точки M и NСкачать  Из точки А проведены две касательные к окружности с центром в точке О?Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 6. Вы открыли страницу вопроса 1) На окружности с центром O и диаметром AB, равным 4, взята точка M, расположенная ближе к точке A, чем к точке B?. Он относится к категории Геометрия. Уровень сложности вопроса – для учащихся 5 — 9 классов. Удобный и простой интерфейс сайта поможет найти максимально исчерпывающие ответы по интересующей теме. Чтобы получить наиболее развернутый ответ, можно просмотреть другие, похожие вопросы в категории Геометрия, воспользовавшись поисковой системой, или ознакомиться с ответами других пользователей. Для расширения границ поиска создайте новый вопрос, используя ключевые слова. Введите его в строку, нажав кнопку вверху. Ответ : 14Пошаговое объяснение : CD = BD — BCCD = 27 + x — (3x + 47) = 27 + x — 3x — 47 = — 2x — 20CE = CD + DE = — 2x — 20 + 10 = — 2x — 10С другой стороны, СЕ = х + 26, x + 26 = — 2x — 103x = — 36x = — 12CE = x + 26 = — 12 + 26 = 14. Решение в приложении. ЕН⊥СН и EF⊥CF. Углы между соответственно перпендикулярными прямыми равны, значит∠FCH = ∠FEH. ВЕ = CF, значит ЕBCF — прямоугольник. BF — диагональ. Точка О — центр описанной окружности около прямоугольника. ∠FCH = ∠FEH значит FH — хорда окружност.. По теореме Пифагора 100 — 73 = 27. Сторона треугольника равна 2 корень из 27, или 6 корень из 3. Треугольник равносторонний. Расстояние от данной точки до плоскости треугольника — расстояние от точки до точки пересечения биссектрис (высот, медиан).. 16 — (5×2) = 6 6÷2 = 3 Друга сторона паралелограма 3см. Sтрап. = ½(17 + 9)×4 = 13×4 = 52см². 12) С 16) А 17) D 18) С. 180 — 90 — 70 = 20 180 — (20 * 2) = 140 — один угол 180 — 140 = 40 — другой угол. 4, 2 / 6 = 0, 7 — будет равны две части, поделенные в серединке. 4, 2 — 0, 7 = 3, 5. Значит угол B = углуD = 120 как противоположные в параллелограмме угол D находится между сторонами AD и DC значит можно воспользоваться формулою площади S = AD * DC * sinD = 12 * 32 / кор3 * кор3 / 2 = 192 см ^ 2 что такое кор3 / 2 это синус120. 📸 Видео№968. Напишите уравнение окружности с центром в точке А(0; 6), проходящей через точку В (-3; 2).Скачать  Точка М лежит на диаметре АВ окружности с центром ОСкачать  Окружность, диаметр, хорда геометрия 7 классСкачать  №644. Прямые МА и MB касаются окружности с центром О в точках А и В. Точка С симметрична точке ОСкачать  Всё про углы в окружности. Геометрия | МатематикаСкачать  |









