Одним из инструментов в области имитационного моделирования является способ решения задач с использованием эксперимента со случайными числами, который носит название метода Монте-Карло. Область применения этого метода и его алгоритм описаны в данной статье.
- Что такое метод Монте-Карло
- Использование метода Монте Карло для вычисления площади фигуры
- Алгоритм вычисления площади фигуры с помощью метода Монте Карло
- Метод Монте-Карло вычисления площадей фигур и его реализация в среде Delphi
- Вычисления площадей геометрических фигур. Метод Монте-Карло.
- Просмотр содержимого документа «Вычисления площадей геометрических фигур. Метод Монте-Карло. »
- 🎥 Видео
Видео:Метод Монте-КарлоСкачать

Что такое метод Монте-Карло
Метод Монте-Карло относится к группе численных методов решения задач, в условиях которых присутствует элемент неопределенности. Он позволяет получить приближенные результаты на множестве входных значений, которые подбираются произвольно путем генерации случайных чисел.
Название этого метода выбрано в честь города Монте-Карло, известного своими казино. Рулетка в казино – это своего рода генератор случайных чисел. Этот метод впервые был описан в 1949 году в совместной работе математиков Николаса Метрополиса и Станислава Улама. Известно, что название придумал Н. Метрополис в честь одного из своих родственников, который был азартным игроком и частым посетителем казино.
Видео:Метод Монте-КарлоСкачать

Использование метода Монте Карло для вычисления площади фигуры
Простым примером иллюстрации применения данного метода является способ определения площади фигуры сложной формы, когда контуры объекта не образуют геометрической формы, для которой существует готовая формула для расчета.
Рис. 2. Фигура сложной формы.
Чтобы вычислить площадь S такой фигуры, ее вписывают в квадрат стороной a. Затем, случайным образом выбирают точки внутри квадрата. Причем точки могут попадать как внутрь исследуемой фигуры сложной формы, так и вне ее.
Чем большую площадь занимает фигура внутри квадрата, тем чаще в нее будут попадать точки. Точки, попавшие внутрь фигуры, обозначают буквой m, а все выбранные точки внутри квадрата – буквой n.
Здесь проявляется закономерность: чем больше точек в эксперименте задействовано, тем с большей вероятностью можно утверждать, что процент точек, содержащихся в исследуемой фигуре стремится к отношению площади фигуры к площади квадрата. Математически это можно записать следующим образом: s=a*a*(m/n).
Таким образом, получен некоторый способ определения площади фигуры произвольной формы с использованием метода статистических испытаний. Модели для вычисления площади различных фигур сложной формы, сформированные этим способом, будут отличаться математическими описаниями фигур.
В теории вероятностей и математической статистике действует закон больших чисел, согласно которому результат эксперимента окажется свободным от случайных воздействий только в случае большого количества случайных факторов, то есть будет прослеживаться устойчивая закономерность. Проще говоря, чем больше число испытаний, тем точнее будет результат.
Видео:Площадь треугольника. Как найти площадь треугольника?Скачать

Алгоритм вычисления площади фигуры с помощью метода Монте Карло
Определим площадь фигуры, ограниченной уравнениями y = x^2, y = 0 и x = 1.
Составим модель: площадь искомой фигуры впишется в квадрат. Если значения координат x и y принадлежит диапазону [0;1], то точка принадлежит квадрату. Если выполняется система неравенств 0 Что мы узнали?
Одним из способов построения моделей является метод статистических испытаний, носящий название Метода Монте Карло. Важным условием применения статистических методов является проведения большого количества испытаний путем генерации случайных входных параметров. С помощью метода Монте Карло можно вычислить площадь фигуры произвольной формы.
Видео:Найдите площадь треугольника на рисунке ★ Два способа решенияСкачать

Метод Монте-Карло вычисления площадей фигур и его реализация в среде Delphi
В начале урока рассказываю идею метода. Ребята, сегодня мы рассмотрим интересный метод приближенного вычисления площадей фигур – метод Монте – Карло. Пусть у нас есть какая – нибудь фигура на плоскости, площадь которой ( Sfig ) нам необходимо найти. Ограничим ее другой фигурой, площадь которой ( Stotal ) мы можем легко вычислить. Например, прямоугольником АСDB со сторонами, параллельными координатным осям (см. рис. 1). И пусть про любую точку прямоугольника мы можем быстро узнать, попадает эта точка внутрь фигуры, площадь которой мы ищем, или нет.
А теперь начнем опыт – будем бросать на бумагу зерна случайным образом (вообще – то это нелегко сделать, чтобы обеспечить случайность). Когда нам покажется, что зерна почти полностью покрыли бумагу, посчитаем, сколько всего зерен на прямоугольнике (пусть их число Ntotal ) и сколько из них на фигуре ( Nfig ). Ясно, что число зерен, попавших внутрь фигуры, пропорционально ее площади: больше площадь – больше зерен, меньше площадь – меньше зерен. Поэтому, поделив количество зерен , попавших внутрь фигуры , на количество всех зерен в прямоугольнике, мы сможем найти, какую часть площади прямоугольника занимает фигура:
Промоделируем этот опыт на ЭВМ. Предположим, нам надо найти площадь фигуры ограниченной сверху кривой Y = F(X), а снизу – осью абсцисс. Пусть Y = cos(X), а Х I [– p /2, p /2] (см. рис. 2). Ограничим нашу фигуру прямоугольником АСDB, его площадь равна p .
Из чего должен состоять алгоритм:
1. Бросание зерна – бросание случайной точки, координаты X и Y которой случайны, причем Х должна меняться от – p /2 до p /2, а Y – от 0 до 1. И в этих интервалах X и Y должны появляться с одинаковой вероятностью в любой точке этих отрезков, т.е. X и Y должны быть равномерно распределены по осям. Тут надо напомнить ребятам, как получить равномерно распределенное случайное вещественное число на интервале [А, В]:
Х = random* ( B – A) + A
2. Надо определить, куда попала точка – под кривую или выше нее. И вести подсчет Nfig. Условие попадания точки под кривую: Y ? sin (X).
3. Повторить пп.1 и 2 столько раз, чтобы получить желаемую точность результатов.
Дети без труда напишут программу по данному алгоритму (на практическом занятии). И после этого наступает момент разочарования. Сухие цифры.
Предложение учителя: давайте создадим проект в Delphi, который наглядно демонстрировал бы работу метода Монте – Карло. Разработаем интерфейс программы. Тут ребята сами предлагают несколько вариантов оформления проекта, один из которых представлен на рис. 3.
Разместим на форме следующие компоненты:
Edit – окно редактирования для ввода общего количества испытаний (бросков зерен) – Ntotal;
Button – кнопка для запуска работы метода Монте – Карло;
Panel – панель для вывода посчитанной площади фигуры;
(все вышеперечисленные компоненты расположены на вкладке Standart Палитры компонентов)
Image – для вывода точек, попавших в искомую область (компонент расположен на вкладке Additional Палитры компонентов).
Если необходимо, надо напомнить ребятам некоторые свойства и методы выбранных компонентов (это может быть и домашним заданием предыдущего урока, чтобы не терять время на “воспоминания”) .
Свойство Text – содержит текст, который пользователь набирает в окне Edit. Этот текст надо преобразовать в число Ntotal. Для этого в Delphi есть необходимая функция StrToInt:
Ntotal = StrToInt (Edit1.Text).
Свойство Caption – содержит текст, который выводится на панель. Чтобы вывести полученное число Sfig на панель, мы должны преобразовать его в строку S с помощью процедуры Str:
а потом вывести эту строку на панель следующим образом:
Panel1.Caption := ‘Площадь фигуры = ‘ + S
Свойства Height и Width – соответственно высота и ширина компонента;
Свойство Canvas – отводит канву (место) для рисования на компоненте Image;
FillRect(ClientRect) – закрашивает область клиента компонента Image каким – либо цветом
(по – умолчанию – белым), т.е. стирает предыдущую картинку;
MoveTo(X, Y) – перемещает перо в точку с координатами X, Y без проведения линии (координаты задаются в пикселях);
LineTo(X, Y) – проводит линию из текущей точки в точку с координатами X, Y;
Pixels[I, J] – содержит цвет точки с координатами I, J.
У кнопки (компонент Button) мы будем обрабатывать событие onClick (событие нажатие кнопки). Т.е. вышеописанный алгоритм мы программируем в процедуре Button1Click.
Тут учитель задает вопрос классу: “ Какая проблема возникает при выводе точки на экран (на компонент Image)?” Ответ: расчетные координаты очень малы (0 ? Y ? 1,меньше пикселя, -p /2 ? X ? p /2); а если взять другую кривую Y = F(X), они могут оказаться слишком большими (больше размера компонента Image). Поэтому, при выводе значений функций (графиков) на экран монитора, необходимо преобразовывать расчетные координаты в графические с учетом дискретности растровой сетки монитора, а также предусмотреть возможность автоматического масштабирования функции (графика) по осям координат. Для этого желательно создать отдельную подпрограмму.
Для полного размещения функции (графика) в расчетной области (это область компонента Image) необходимо определить X_min, X_max, Y_min, Y_max – минимальные и максимальные значения по X и по Y соответственно. X_min =А, X_max = В. Как найти Y_min, Y_max.
Коллективно обсуждается следующий алгоритм:
1. Разобьем интервал [А, В] по Х на N равных частей и определим массивы значений аргумента и функции X[i] и Y[i] = F(X[i]), где I = 1..N;
2. Определяем наибольшее Y_max и наименьшее Y_min значения функции в заданном интервале изменения аргумента;
3. Находим коэффициенты масштабирования Kx, Ky при построении графика в заданной области;
4. Т.к. коэффициенты масштабирования Kx, Ky могут отличаться, то выводимый график может искажаться. Устраняем искажения графика;
5. Преобразуем расчетные координаты точки X, Y в графические Xg, Yg. С учетом того, необходимости “переворота” оси Y, которая в координатах монитора направлена сверху вниз.
Листинг программы, реализующей данные алгоритмы представлен в конце статьи. Результат работы программы при разном количестве испытаний представлен на рис. 3, 4.
Задания для самостоятельной работы:
1. Применить метод Монте – Карло для приближенного вычисления площади фигуры, ограниченной сверху кривой Y = sin (X), при Х I [ 0, p ];
2. Применить метод Монте – Карло для приближенного вычисления числа p . Подсказка: рассмотреть круг единичного радиуса с центром в т. (1, 1). Его площадь и будет равна p .
3. Применить метод Монте – Карло для приближенного вычисления площади фигуры, ограниченной сверху кривой Y = sin (X), при Х I [ 0, 2p ];
4. Применить метод Монте – Карло для приближенного вычисления площадей фигур, представленных на рис. 5 – 7. 


5. Доработать проект:
а) организавать проверку правильности ввода информации в поле Edit (чтобы вводились только целые числа);
б) разметить оси и подписать числовые значения.
На последующих уроках, на которых предполагается изучение тем “Вычисление площадей (интегралов) методом трапеций и методом прямоугольников”, можно предложить ребятам доработать проект, поместив на форму дополнительные компоненты Image, Button, Edit, Panel (для каждого численного метода – свои). В окно компонента Edit пользователь будет вводить количество разбиений интервала [А, В] по Х. Таким образом, ребята смогут сравнить и наглядно увидеть работу всех трех численных методов.
unit Monte;
interface
uses
Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,
Dialogs, StdCtrls, ExtCtrls, Buttons;
type
TForm1 = class(TForm)
Panel1: TPanel;
BitBtn1: TBitBtn;
Edit1: TEdit;
Label1: TLabel;
Image1: TImage;
const A = -Pi/2.0; B = pi/2.0; n = 1000;
var
Form1: TForm1;
N_total:longint;
implementation
Function FUNC(x:real):real;
begin
Func:=Cos(x);
end;
Procedure Graphic( var right, down: integer;
var X_min, X_max, Y_min, Y_max, Kx, Ky: real);
type arr=array[1..n] of real;
var
X, Y: arr; dx: real;
i: integer;
begin
dx:=(B-A)/(n-1);
for i:=1 to n do begin X[i]:=A+dx*(i-1);
Y[i]:=FUNC(X[i]);
end;
X_max:=B; X_min:=A;
Y_max:=Y[1]; Y_min:=Y[1];
for i:=2 to n do begin
if Y_max Y[i] then Y_min:=Y[i];
end;
Видео:Что такое метод Монте-Карло (простым языком)Скачать

Вычисления площадей геометрических фигур. Метод Монте-Карло.
Вычисления площадей геометрических фигур. Метод Монте-Карло.
Цель работы: освоить понятие метода Монте-Карло, как основного метода создания вероятностных моделей;
Задачи:
1.yаучиться вычислять площади нестандартных фигур используя среду программирования Pascal и электронные таблицы Excel;
2.уметь записывать предикат для фигуры, площадь которой необходимо найти
3.cравнить полученные результаты;
Просмотр содержимого документа
«Вычисления площадей геометрических фигур. Метод Монте-Карло. »
Различные способы вычисления
Автор: Розова Е.Е., учитель информатики МОУ гимназии№3 им. А.Н.Островского г. Кинешма, Ивановской обл.
Цель работы: освоить понятие метода Монте-Карло, как основного метода создания вероятностных моделей;
- Научиться вычислять площади нестандартных фигур используя среду программирования Pascal и электронные таблицы Excel;
- уметь записывать предикат для фигуры, площадь которой необходимо найти
- Сравнить полученные результаты;
Математический способ определения площади фигуры ( домашнее задание )
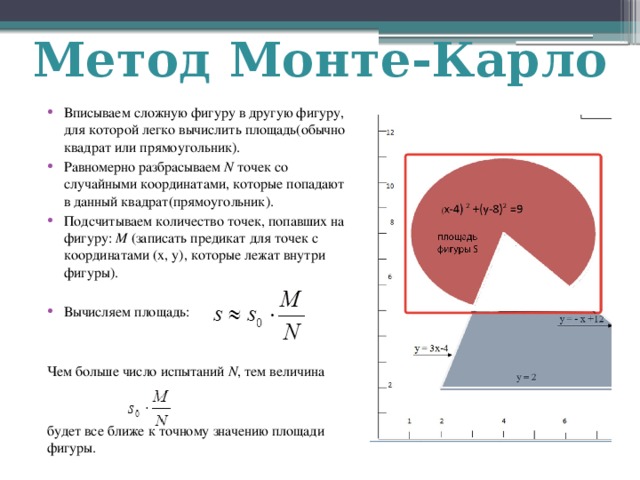
- Вписываем сложную фигуру в другую фигуру, для которой легко вычислить площадь(обычно квадрат или прямоугольник).
- Равномерно разбрасываем N точек со случайными координатами, которые попадают в данный квадрат(прямоугольник).
- Подсчитываем количество точек, попавших на фигуру: M (записать предикат для точек с координатами (x, y), которые лежат внутри фигуры).
- Вычисляем площадь:
Чем больше число испытаний N , тем величина
будет все ближе к точному значению площади фигуры.
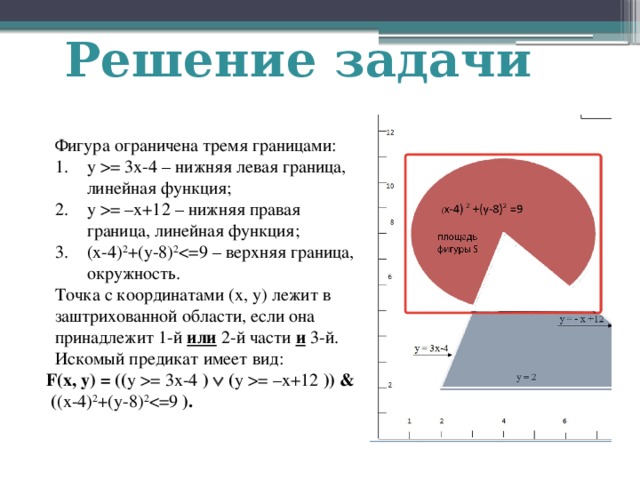
Фигура ограничена тремя границами:
- y = 3x-4 – нижняя левая граница, линейная функция;
- y = –x+12 – нижняя правая граница, линейная функция;
- (x-4) 2 +(y-8) 2
Точка с координатами (x, y) лежит в заштрихованной области, если она принадлежит 1-й или 2-й части и 3-й.
🎥 Видео
9 класс, 12 урок, Теорема о площади треугольникаСкачать

Как найти площадь треугольника без формулы?Скачать

8 класс, 14 урок, Площадь треугольникаСкачать

Этой задачей русские дети 10 лет мучили американцев. Американцы не понимали, что делают не такСкачать

Управление рисками Метод Монте КарлоСкачать

👉 ФОРМУЛА ГЕРОНА. Площадь треугольника #shortsСкачать

Реализация метода Монте Карло расчет площади круга программаСкачать

Площадь фигуры через двойной интеграл в полярных координатахСкачать

Найдите площадь треугольника АВС, если А(5;2;6), В(1;2;0), С(3;0;3)Скачать

Самый короткий тест на интеллект Задача Массачусетского профессораСкачать

Запомни: все формулы для площади треугольникаСкачать

Задача, которую исключили из экзамена в АмерикеСкачать

МЕТОД МОНТЕ-КАРЛО. КАК ВЫЧИСЛИТЬ ПЛОЩАДЬ КЛЕНОВОГО ЛИСТА?Скачать

Интегрирование методом Монте КарлоСкачать

3.3 Определенный интеграл. Метод Монте-Карло. Часть 1.Скачать