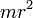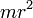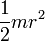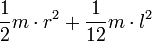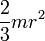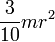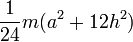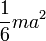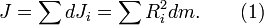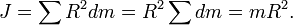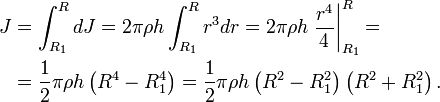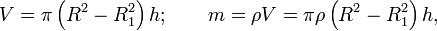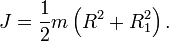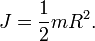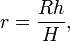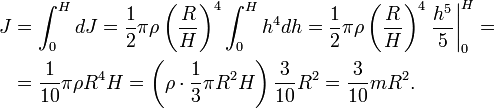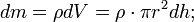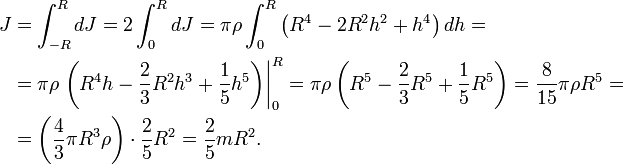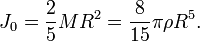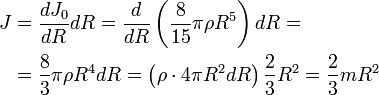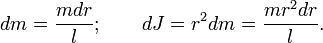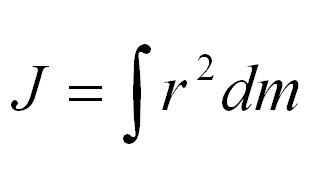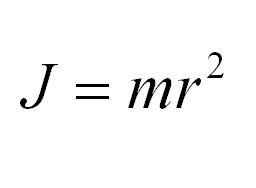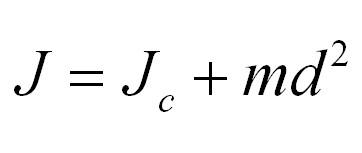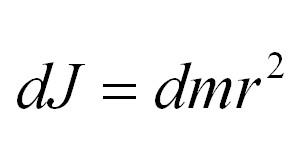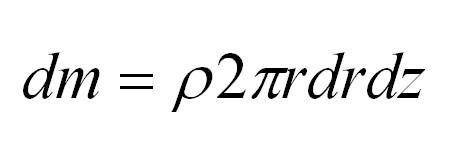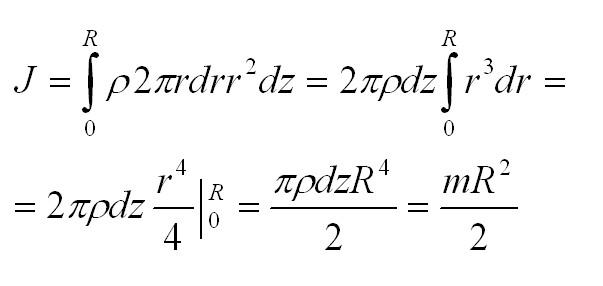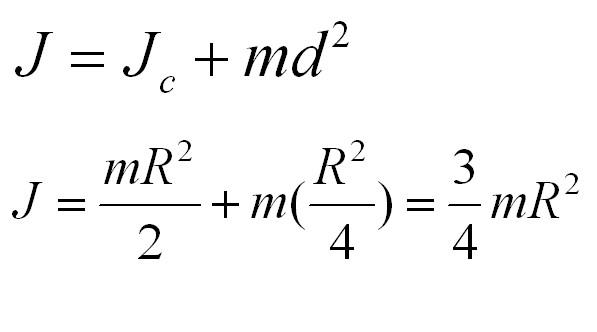Момент инерции окружности относительно ее центра (7 видео)

Определение моментов инерции с помощью круга инерции

Формулы (2.13) для случая, когда в качестве исходных приняты главные оси, имеют простую геометрическую интерпретацию. Если ввести обозначения

то указанные формулы примут вид

Из этих формул видно, что момент инерции J_y может быть получен из выражения для / заменой а на а + 90°.

Первая и третья из формул (2.24) представляют собой параметрические уравнения окружности в координатных осях J_x, J^ с радиусом R и центром на оси / на расстоянии а от начала координат (рис. 2.20). Абсцисса произвольной точки К_х этой окружности равна осевому моменту инерции J_x относительно оси Ох, которая составляет угол ос с главной осью 1 (см. рис. 2.7). Ордината точки К_х равна центробежному моменту инерции J относительно осей Ох, Оу.

Координаты точки ^окружности, называемой полюсом, равны соответственно J_y и J_xy.

Впервые данный графический способ был предложен О. Мором для определения напряжений на наклонных площадках (см. § 4.6), и соответствующий круг называется кругом Мора для напряжений. По аналогии круг, изображенный на рис. 2.20, называется кругом инерции.

С помощью круга инерции можно графически определить моменты инерции относительно произвольных осей. При этом обычно строят круг инерции по известным моментам инерции J_x, J_y, J_xy,

вычисленным относительно произвольных осей Ох и Оу. Приведем это построение (рис. 2.21).

Тангенсы углов наклона главных осей 1 и 2 к оси Ох определяются из прямоугольных треугольников ВЕК и ВАК:

На горизонтальной оси отложим OD = J_x и OB = J_y. Поделив отрезок BD пополам, получим центр круга инерции С, причем OC=(J_x + J_y)/2. Отложив из конца отрезка OB = J_y величину / = ВК со своим знаком, получим полюс К круга инерции. Проводя радиусом С К окружность и далее через полюс ^Глучи КЕ и КА, найдем величины главных моментов инерции J_l = ОЕ, /₂ = ОА и углы наклона 0Cj и ос₂ главных осей 1 и 2 к оси Ох.

С помощью приведенных на рис. 2.21 построений можно получить формулы для величин главных моментов инерции (2.12) и углов наклона главных осей (2.11). Действительно, определив из прямоугольного треугольника ВСКрадиус круга инерции

Знак минус в первой формуле объясняется тем, что угол а, является отрицательным.

Для определения величин моментов инерции J , J , J от-

носительно произвольных взаимно перпендикулярных осей Ох_< и Оу_х, наклоненных к оси Ох на угол (3, необходимо через полюс К провести под углом (3 к горизонтали ось Ох_х и перпендикулярно к ней — ось Оу_х до пересечения этих осей с окружностью в точках М и N. Можно показать, что искомые величины моментов инерции соответственно равны

В качестве иллюстрации на рис. 2.22 приведено построение круга инерции для числового примера 2.1, рассмотренного в § 2.7.

Содержание

Строительный клуб
Как найти момент инерции круга?
Как вывести формулу момента инерции
Что такое инерция
Определение момента инерции
Теорема Штейнера
Пример решения задачи на нахождение момента инерции
💥 Видео

Видео:Урок 94. Вычисление моментов инерции телСкачать

Строительный клуб

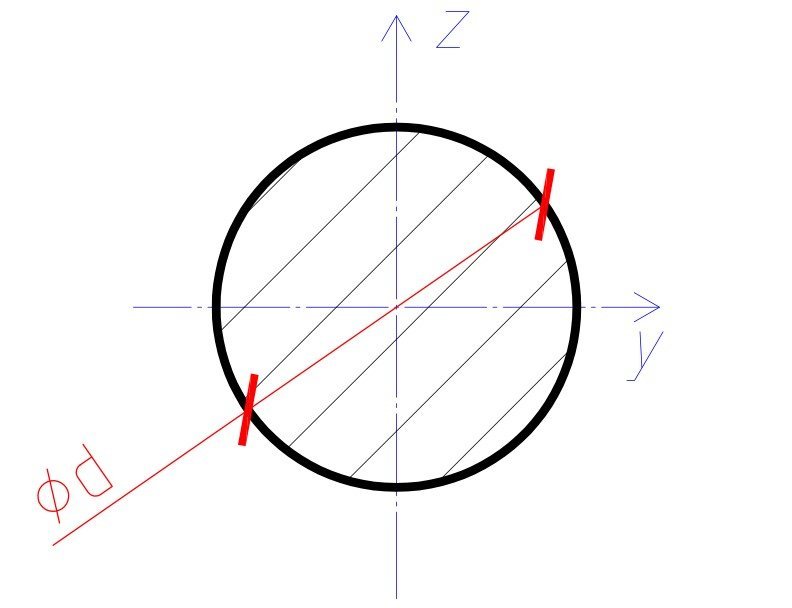
d — диаметр сечения круга в мм; y, z — центральные оси сечения.

Введите диаметр сечения d в мм:

В результате момент инерции относительно центральных осей y и z равны I_y = I _z =

Видео:Момент инерцииСкачать

Как найти момент инерции круга?

Момент инерции круга относительно центральной оси z равен моменту инерции относительно центральной оси y и рассчитывается по формуле:

l_y = l_z = Π . d 4 /64 ,

l_y — момент инерции относительно центральной оси y в мм 4 ;

l_z — момент инерции относительно центральной оси z в мм 4 ;

d — диаметр круга в мм.

Видео:Расчёт момента инерции тела относительно оси вращения. Момент инерции однородного стержняСкачать

Как вывести формулу момента инерции

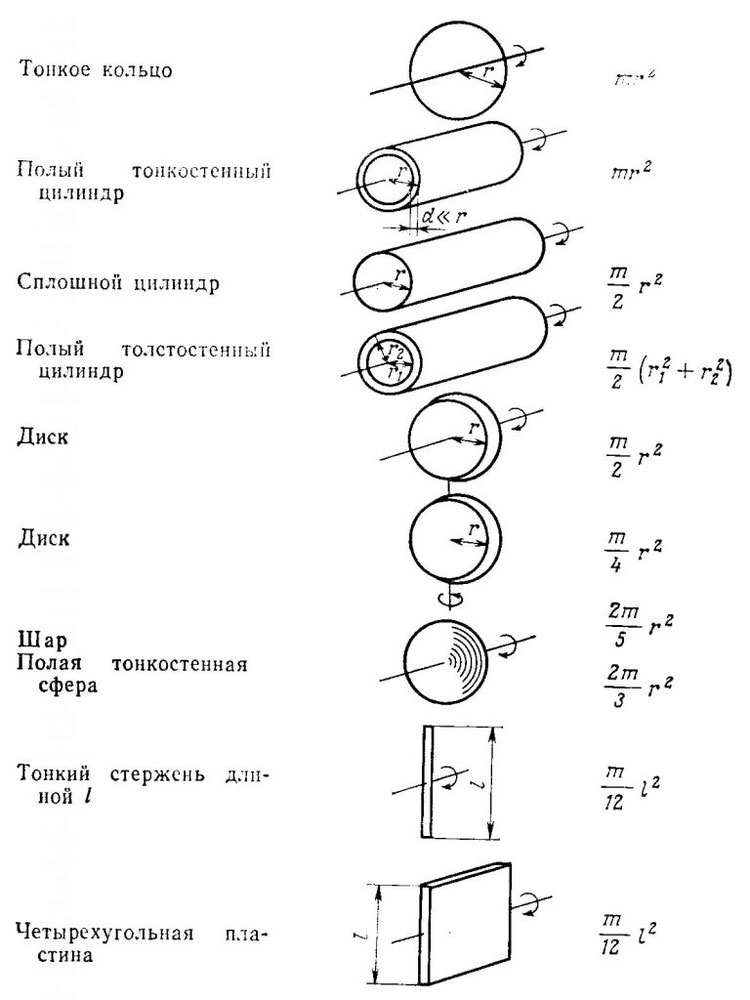
Осевые моменты инерции некоторых тел

Моменты инерции однородных тел простейшей формы относительно некоторых осей вращения

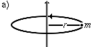
Материальная точка массы m

На расстоянии r от точки, неподвижная

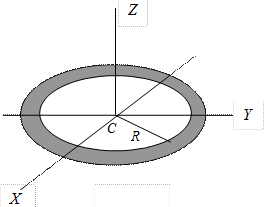
Полый тонкостенный цилиндр или кольцо радиуса r и массы m

Сплошной цилиндр или диск радиуса r и массы m

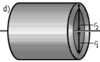
Полый толстостенный цилиндр массы m с внешним радиусом r₂ и внутренним радиусом r₁

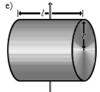
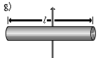
Сплошной цилиндр длины l, радиуса r и массы m

Ось перпендикулярна к цилиндру и проходит через его центр масс

Полый тонкостенный цилиндр (кольцо) длины l, радиуса r и массы m

Ось перпендикулярна к цилиндру и проходит через его центр масс

Прямой тонкий стержень длины l и массы m

Ось перпендикулярна к стержню и проходит через его центр масс

Тонкостенная сфера радиуса r и массы m

Ось проходит через центр сферы

Шар радиуса r и массы m

Ось проходит через центр шара

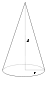
Конус радиуса r и массы m

Равнобедренный треугольник с высотой h, основанием a и массой m

Ось перпендикулярна плоскости треугольника и проходит через вершину

Правильный треугольник со стороной a и массой m

Ось перпендикулярна плоскости треугольника и проходит через центр масс

Квадрат со стороной a и массой m

Ось перпендикулярна плоскости квадрата и проходит через центр масс

Тонкостенный цилиндр (кольцо, обруч)

Момент инерции тела равен сумме моментов инерции составляющих его частей. Разобъём тонкостенный цилиндр на элементы с массой dm и моментами инерции dJ_i. Тогда

Поскольку все элементы тонкостенного цилиндра находятся на одинаковом расстоянии от оси вращения, формула (1) преобразуется к виду

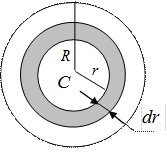
Толстостенный цилиндр (кольцо, обруч)

Пусть имеется однородное кольцо с внешним радиусом R, внутренним радиусом R₁, толщиной h и плотностью ρ. Разобьём его на тонкие кольца толщиной dr. Масса и момент инерции тонкого кольца радиуса r составит

Момент инерции толстого кольца найдём как интеграл

Поскольку объём и масса кольца равны

получаем окончательную формулу для момента инерции кольца

Однородный диск (сплошной цилиндр)

Рассматривая цилиндр (диск) как кольцо с нулевым внутренним радиусом (R₁ = 0), получим формулу для момента инерции цилиндра (диска):

Разобьём конус на тонкие диски толщиной dh, перепендикулярные оси конуса. Радиус такого диска равен

где R – радиус основания конуса, H – высота конуса, h – расстояние от вершины конуса до диска. Масса и момент инерции такого диска составят

Сплошной однородный шар

Разобъём шар на тонкие диски толщиной dh, перпендикулярные оси вращения. Радиус такого диска, расположенного на высоте h от центра сферы, найдём по формуле

Масса и момент инерции такого диска составят

Момент инерции сферы найдём интегрированием:

Для вывода воспользуемся формулой момента инерции однородного шара радиуса R:

Вычислим, насколько изменится момент инерции шара, если при неизменной плотности ρ его радиус увеличится на бесконечно малую величину dR.

Тонкий стержень (ось проходит через центр)

Разобъём стержень на малые фрагменты длиной dr. Масса и момент инерции такого фрагмента равна

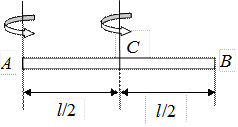
Тонкий стержень (ось проходит через конец)

При перемещении оси вращения из середины стержня на его конец, центр тяжести стержня перемещается относительно оси на расстояние l/2. По теореме Штейнера новый момент инерции будет равен

Момент инерции тела относительно какой-либо оси можно найти вычислением. Если вещество в теле распределено непрерывно, то вычисление момента инерции его сводится к вычислению интеграла

, (4.14)

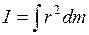
в котором r – расстояние от элемента массы dm до оси вращения.

Момент инерции тонкого однородного стержня относительно перпендикулярной оси. Пусть ось проходит через конец стержня А (рис. 4.4).

Для момента инерции можно написать I_A = kml 2 , где l – длина стержня, k – коэффициент пропорциональности. Центр стержня С является его центром масс. По теореме Штейнера I_A = I_C + m(l/2) 2 . Величину I_C можно представить как сумму моментов инерции двух стержней, СА и СВ, длина каждого из которых равна l/2, масса m/2, а следовательно, момент инерции равен 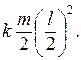Таким образом, I_C = km(l/2) 2 . Подставляя эти выражения в формулу для теоремы Штейнера, получим

откуда k = 1/3. В результате находим

(4.15)

(4.16)

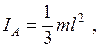
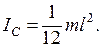
Момент инерции бесконечно тонкого круглого кольца (окружности). Момент инерции относительно оси Z (рис. 4.5) равен

где R – радиус кольца. Ввиду симметрии I_X = I_У.

Формула (4.17) очевидно, дает также момент инерции полого однородного цилиндра с бесконечно тонкими стенками относительно его геометрической оси.

Момент инерции бесконечно тонкого диска и сплошного цилиндра. Предполагается, что диск и цилиндр однородны, т. е. вещество распределено в них с постоянной плотностью. Пусть ось Z проходит через центр диска С перпендикулярно к его плоскости (рис. 4.6). Рассмотрим бесконечно тонкое кольцо с внутренним радиусом r и наружным радиусом r + dr. Площадь такого кольца dS = 2prdr. Его момент инерции найдется по формуле (4.17), он равен dI_z = r 2 dm. 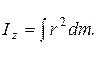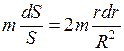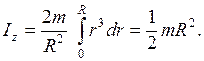Момент инерции всего диска определяется интегралом Ввиду однородности диска dm = , где S = pR 2 – площадь всего диска. Вводя это выражение под знак интеграла, получим

(4.18)

Формула (4.18) дает также момент инерции однородного сплошного цилиндра относительно его продольной геометрической оси.

Вычисление момента инерции тела относительно оси часто можно упростить, вычислив предварительно момент инерции его относительно точки. Сам по себе момент инерции тела относительно точки не играет никакой роли в динамике. Он является чисто вспомогательным понятием, служащим для упрощения вычислений. Моментом инерции тела относительно точки О называется сумма произведений масс материальных точек, из которых тело состоит, на квадраты их расстояний R до точки О: q = ΣmR 2 . В случае непрерывного распределения масс эта сумма сводится к интегралу q = ∫R 2 dm. Само собой понятно, что момент θ не следует смешивать с моментом инерции I относительно оси. В случае момента I массы dm умножаются на квадраты расстояний до этой оси, а в случае момента θ – до неподвижной точки.

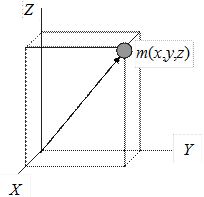
Рассмотрим сначала одну материальную точку с массой m и с координатами x, у, z относительно прямоугольной системы координат (рис. 4.7). Квадраты расстояний ее до координатных осей Х, Y, Z равны соответственно у 2 + z 2 , z 2 + x 2 , x 2 + у 2 , а моменты инерции относительно тех же осей

Но х 2 + у 2 + z 2 = R 2 , где R – расстояние точки m от начала координат О. Поэтому

Это соотношение справедливо не только для одной материальной точки, но и для произвольного тела, так как тело можно рассматривать как совокупность материальных точек. Таким образом, сумма моментов инерции тела относительно трех взаимно перпендикулярных осей, пересекающихся в одной точке О, равна удвоенному моменту инерции того же тела относительно этой точки.

Момент инерции полого шара с бесконечно тонкими стенками.

Сначала найдем момент инерции θ относительно центра шара. Очевидно, он равен θ = mR 2 . Затем применяем формулу (4.19). Полагая в ней ввиду симметрии I_X = I_Y = I_Z = I. В результате находим момент инерции полого шара относительно его диаметра

. (4.20)

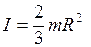
Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Увлечёшься девушкой-вырастут хвосты, займёшься учебой-вырастут рога 9812 – | 7680 – или читать все.

78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Часто мы слышим выражения: «он инертный», «двигаться по инерции», «момент инерции». В переносном значении слово «инерция» может трактоваться как отсутствие инициативы и действий. Нас же интересует прямое значение.

Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.

Видео:Момент импульса и момент силы относительно точки и оси | Студенты, абитуриенты МФТИ | Вуз. физика #1Скачать

Что такое инерция

Согласно определению инерция в физике – это способность тел сохранять состояние покоя или движения в отсутствие действия внешних сил.

Если с самим понятием инерции все понятно на интуитивном уровне, то момент инерции – отдельный вопрос. Согласитесь, сложно представить в уме, что это такое. В этой статье Вы научитесь решать базовые задачи на тему «Момент инерции».

Видео:5. Момент инерции простейших телСкачать

Определение момента инерции

Из школьного курса известно, что масса – мера инертности тела. Если мы толкнем две тележки разной массы, то остановить сложнее будет ту, которая тяжелее. То есть чем больше масса, тем большее внешнее воздействие необходимо, чтобы изменить движение тела. Рассмотренное относится к поступательному движению, когда тележка из примера движется по прямой.

По аналогии с массой и поступательным движением момент инерции – это мера инертности тела при вращательном движении вокруг оси.

Момент инерции – скалярная физическая величина, мера инертности тела при вращении вокруг оси. Обозначается буквой J и в системе СИ измеряется в килограммах, умноженных на квадратный метр.

Как посчитать момент инерции? Есть общая формула, по которой в физике вычисляется момент инерции любого тела. Если тело разбить на бесконечно малые кусочки массой dm, то момент инерции будет равен сумме произведений этих элементарных масс на квадрат расстояния до оси вращения.

Это общая формула для момента инерции в физике. Для материальной точки массы m, вращающейся вокруг оси на расстоянии r от нее, данная формула принимает вид:

Видео:Вращательное движение. 10 класс.Скачать

Теорема Штейнера

От чего зависит момент инерции? От массы, положения оси вращения, формы и размеров тела.

Теорема Гюйгенса-Штейнера – очень важная теорема, которую часто используют при решении задач.

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Теорема Гюйгенса-Штейнера гласит:

Момент инерции тела относительно произвольной оси равняется сумме момента инерции тела относительно оси, проходящей через центр масс параллельно произвольной оси и произведения массы тела на квадрат расстояния между осями.

Для тех, кто не хочет постоянно интегрировать при решении задач на нахождение момента инерции, приведем рисунок с указанием моментов инерции некоторых однородных тел, которые часто встречаются в задачах:

Видео:Геометрические характеристики. Моменты инерции. Радиусы инерции. Сопромат.Скачать

Пример решения задачи на нахождение момента инерции

Рассмотрим два примера. Первая задача – на нахождение момента инерции. Вторая задача – на использование теоремы Гюйгенса-Штейнера.

Задача 1. Найти момент инерции однородного диска массы m и радиуса R. Ось вращения проходит через центр диска.

Разобьем диск на бесконечно тонкие кольца, радиус которых меняется от до R и рассмотрим одно такое кольцо. Пусть его радиус – r, а масса – dm. Тогда момент инерции кольца:

Массу кольца можно представить в виде:

Здесь dz – высота кольца. Подставим массу в формулу для момента инерции и проинтегрируем:

В итоге получилась формула для момента инерции абсолютного тонкого диска или цилиндра.

Задача 2. Пусть опять есть диск массы m и радиуса R. Теперь нужно найти момент инерции диска относительно оси, проходящей через середину одного из его радиусов.

Момент инерции диска относительно оси, проходящей через центр масс, известен из предыдущей задачи. Применим теорему Штейнера и найдем:

Кстати, в нашем блоге Вы можете найти и другие полезные материалы по физике и решению задач.

Надеемся, что Вы найдете в статье что-то полезное для себя. Если в процессе расчета тензора инерции возникают трудности, не забывайте о студенческом сервисе. Наши специалисты проконсультируют по любому вопросу и помогут решить задачу в считанные минуты.