Момент импульса точки на окружности

При рассмотрении кинематики движения точки по окружности (см. § 27 гл. 1) было установлено, что ускорение точки целесообразно разложить на нормальную _n и тангенциальную _τ составляющие, модули которых соответственно равны:

Нормальная составляющая характеризует изменение скорости только по направлению, а тангенциальная — только по модулю. Соответственно второй закон Ньютона для проекций _n и _τ ускорения запишется так:

где F_n — проекция силы на направление, перпендикулярное скорости, a F_τ — проекция силы на направление скорости.

Второе из этих уравнений перепишем, используя связь тангенциального α_τ и углового β ускорений (α_τ = βR):

Момент силы

Пусть к материальной точке приложена сила, действующая в плоскости движения.

Угловое ускорение, как это следует из уравнения (7.6.1), определяется тангенциальной составляющей силы . Например, силы ₁, ₂, ₃ (рис. 7.30) создают одно и то же ускорение β, так как для них составляющие _τ одинаковы.

Обозначим через α угол между вектором силы и радиусом-вектором рассматриваемой материальной точки. Тогда

Назовем расстояние d между центром окружности О и линией действия силы плечом силы. Из рисунка 7.31 видно, что

В частности, для силы F₁ (см. рис. 7.30) угол α = 90° и, следовательно, d₁ = R, т. е. плечо силы равно радиусу окружности.

Произведение модуля F_τ тангенциальной составляющей на радиус R назовем моментом силы и обозначим буквой М.

Из формул (7.6.2) и (7.6.3) следует, что

Запишем уравнение (7.6.1) в другой форме, используя понятие момента силы. Для этого умножим левую и правую части этого уравнения на R. На основании равенства (7.6.4) получим:

Таким образом, при постоянных значениях m и R момент силы определяет угловое ускорение.

Однако с таким же успехом при заданном R угловое ускорение может определяться величинами F_τR 2 , F_τR 3 и т. д. Поэтому возникает вопрос о том, почему мы выбираем в качестве характеристики силового воздействия именно момент силы М = F_τR, а не какую-либо другую комбинацию величин F_τ, R. Причина такого выбора состоит в следующем.

Сравним движение материальной точки по окружности с прямолинейным движением. Между кинематическими характеристиками в этих случаях имеется следующее соответствие: линейному перемещению Δs соответствует угловое перемещение Δφ, линейной скорости v — угловая скорость ω, линейному ускорению а — угловое ускорение β.

Каково же будет соответствие между динамическими характеристиками? Начнем с силы. Рассмотрим выражение для работы. При движении по окружности работа совершается тангенциальной составляющей ₁ силы. Нормальная составляющая не совершает работы.

Таким образом, при перемещении по окружности на малое расстояние Δs (рис. 7.32) совершается элементарная работа

Введем вместо линейной характеристики перемещения Δs угловое Δφ. Они связаны равенством Δs = RΔφ.

Используя это соотношение, перепишем выражение (7.6.6) в виде:

Отсюда следует, что если вместо линейного перемещения использовать угловое, то роль силы будет играть величина F_τR, т.е. момент силы М.

Знак момента силы

В определении момента силы (7.6.4) не учтено, что сила имеет направление и может как увеличивать угловую скорость, так и уменьшать ее. Это обстоятельство можно учесть так. Будем считать одно из направлений обращения точки, например против движения часовой стрелки, положительным. Тогда моменту силы условимся приписывать знак плюс, если сила увеличивает скорость обращения точки в направлении против часовой стрелки, и знак «минус» в противоположном случае.

Момент инерции

Мы установили, что при описании движения по окружности вместо величин г, v, a, F удобнее использовать величины φ, ω, β, М. Какая же величина соответствует массе? Из уравнения (7.6.5) видно, что роль массы при движении по окружности играет величина mR 2 . Назовем ее моментом инерции и обозначим буквой J:

Используя это обозначение, запишем уравнение движения материальной точки по окружности в форме:

Итак, мерой инертности при движении материальной точки по окружности служит момент инерции. То, что инертность при движении по окружности зависит от радиуса, легко почувствовать. Например, камень на длинной веревке раскрутить труднее, чем на короткой.

Подчеркнем еще раз, что исходное уравнение движения mа₁ = F₁ и уравнение (7.6.9) эквивалентны. Использование того или иного из них при описании движения материальной точки определяется соображениями удобства и простоты.

Момент импульса

В главе 2, посвященной второму закону Ньютона, были рассмотрены две формы записи уравнения движения:

Из второго уравнения (7.6.10) следует, что изменение вектора импульса m определяется импульсом силы dt. Такая форма записи очень удобна при решении многих задач.

Запишем в соответствующем виде уравнение движения материальной точки по окружности. Для этого преобразуем левую часть уравнения (7.6.9).

По определению угловое ускорение . Учитывая, что момент инерции материальной точки J = mR 2 не зависит от времени, можем записать:

Выясним физический смысл величины Jω. Перепишем это выражение в иной форме. Так как J = mR 2 и Rω = v, то

Выражение mvR естественно назвать моментом импульса.

Используя равенство (7.6.11), уравнение (7.6.9) можем записать в виде:

Приходим к выводу: изменение момента импульса определяется импульсом момента силы, т. е. величиной Mdt.

Для момента импульса будем использовать специальное обозначение Jω = L. Тогда уравнение (7.6.13) примет вид:

где L = Jω = mvR — момент импульса. Скоро мы увидим, что момент импульса, подобно импульсу, сохраняется в замкнутых системах.

Для динамического описания движения материальной точки по окружности мы ввели новые величины: момент силы, момент инерции и момент импульса. Был записан второй закон Ньютона в новой форме. Эта форма чрезвычайно удобна для перехода к динамике вращательного движения твердого тела.

Видео:Момент импульса. 10 класс.Скачать

§ 2.7. Момент импульса

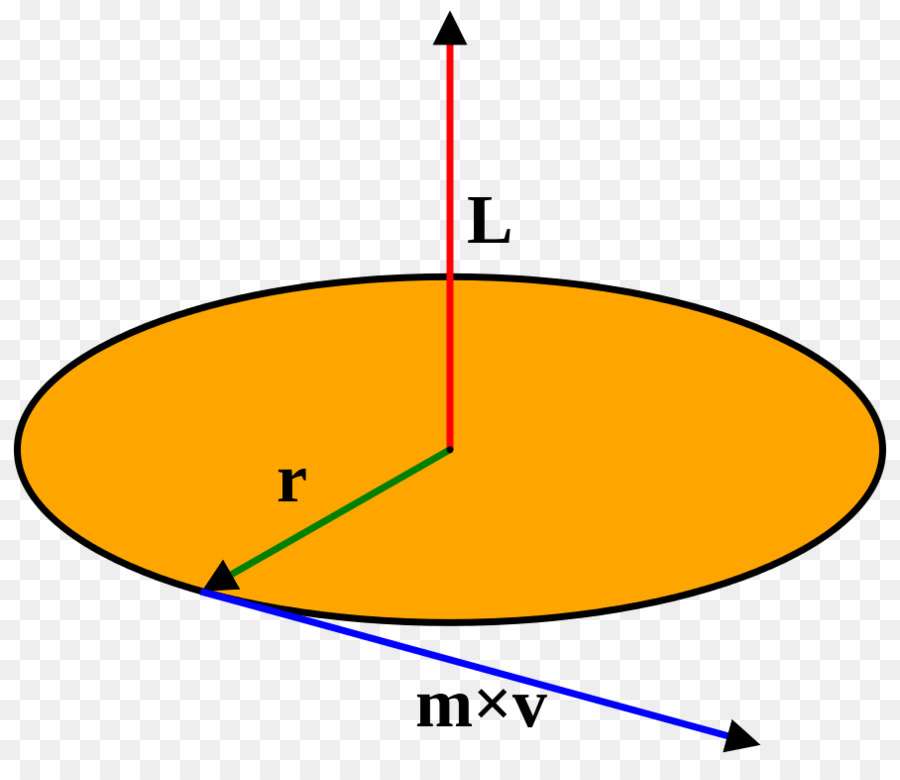
1. Пусть материальная точка массой т движется по окружности радиусом г со скоростью v (рис. 2.5), ее импульс р = т [см. (2.3)]. Моментом импульса L материальной точки относительно центра О называют произведение модуля ее импульса на радиус окружности:

Момент импульса L — это вектор, перпендикулярный плоскости, в которой лежат импульс р и радиус-вектор г (см. рис. 2.5).

2. Пусть на материальную точку массой т действует сила F, составляющая угол а с радиусом окружности г (рис. 2.6). Разложим эту силу на две составляющие: нормальную F„ = F cos а и тангенциальную F_X = F sin а. Нормальная составляющая силы сообщает материальной точке нормальное (центростремительное) ускорение, вызывая поворот тела, но не меняя модуля скорости; тангенциальная составляющая сообщает материальной точке тангенциальное ускорение, т. е. меняет модуль скорости, не меняя ее направления. Итак, согласно второму закону Ньютона (2.13),

3. Пусть модуль момента импульса L [см. (2.24)] изменяется в течение промежутка времени At; при этом следует учесть, что здесь радиус и масса — величины постоянные. Тогда можно записать:

представляющее собой произведение силы F на плечо d (см. рис. 2.6), называют моментом силы. Из (2.25) и (2.26) получим

изменение момента импульса за единицу времени равно моменту силы.

Этот результат аналогичен выражению (2.12), согласно которому изменение импульса за единицу времени равно силе. Поэтому выражение (2.27) называют иногда вторым законом Ньютона для вращательного движения.

4. Если суммарный момент сил, действующих на систему, равен нулю, то изменение вектора момента импульса за единицу времени, согласно (2.27), тоже равно нулю, а это означает, что момент импульса является постоянной величиной, т. е. не меняется ни по модулю, ни по направлению. Оказывается, что наряду с законом сохранения импульса (см. § 2.2) справедлив закон сохранения момента импульса, который формулируется так:

Суммарный момент импульса замкнутой системы в результате действия внутренних сил не меняется.

Закон сохранения момента импульса является столь же фундаментальным законом природы, как и закон сохранения импульса. Справедливость этих законов подтверждается всей совокупностью физических знаний.

Таким образом, если внешние силы не действуют на уже вращающееся тело, иными словами, момент сил М= 0, то AL = 0, т. е. вектор момента импульса L уже вращающегося тела не изменяется ни по модулю, ни по направлению.

Так, можно наблюдать вращающихся конькобежца или балерину. Это значит, что у них вектор момента импульса вдоль оси симметрии остается постоянным. При отсутствии трения их вращение продолжалось бы бесконечно долго.

На этом же принципе работает гироскоп. Гироскопом называют всякое тело вращения, которое вращается вокруг точки, лежащей на оси симметрии тела.

Гироскоп нашел широкое применение на практике. Например, гироскоп на спутнике сохраняет в космосе его положение относительно Солнца; гироскоп на корабле до некоторой степени успокаивает его качку; установив ось гироскопа в направлении север—юг, имеют так называемый гирокомпас. Используя гирокомпас, можно поддерживать заданное направление корабля («авторулевой») или самолета («автопилот»). Гироскопом является сам снаряд или пуля, вылетающие из винторезного ствола. В полете они сохраняют направление оси симметрии. В боевых морских торпедах устанавливают гироскоп для сохранения направления на цель после их пуска и т. д.

Видео:Урок 109. Момент импульса. Закон сохранения момента импульсаСкачать

Закон сохранения момента импульса: формула, применение и особенности

При решении задач на движение тел в пространстве часто используют формулы сохранения кинетической энергии и импульса. Оказывается, что аналогичные выражения существуют и для вращающихся тел. В данной статье подробно рассматривается закон сохранения момента импульса (формулы соответствующие также приводятся) и дается пример решения задачи.

Видео:Момент импульса и момент силы относительно точки и оси | Студенты, абитуриенты МФТИ | Вуз. физика #1Скачать

Процесс вращения и момент импульса

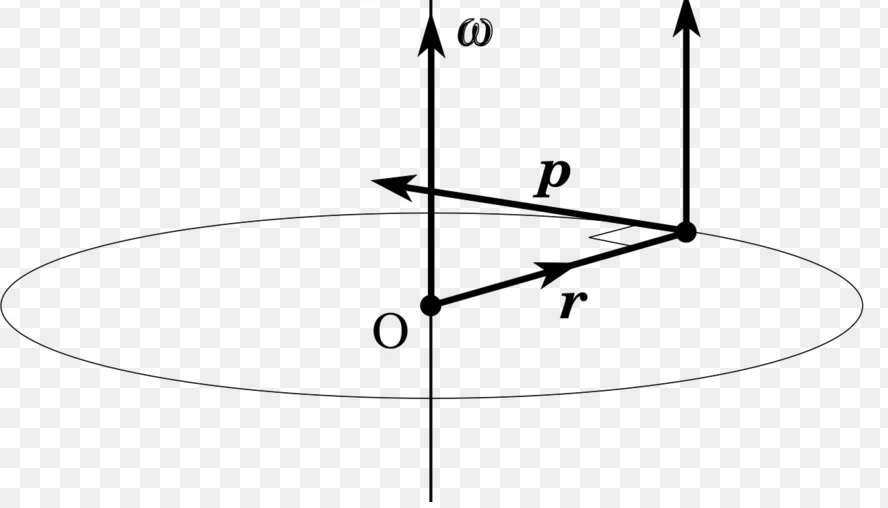
Перед тем как перейти к рассмотрению формулы закона сохранения момента импульса, необходимо познакомиться с этим физическим понятием. Проще всего его можно ввести, если воспользоваться рисунком ниже.

Вам будет интересно: Нарративный анализ: понятие и применение

На рисунке видно, что на конце вектора r¯, направленного от оси вращения и перпендикулярного ей, имеется некоторая материальная точка массой m. Эта точка движется по окружности названного радиуса с линейной скоростью v¯. Из физики известно, что произведение массы на линейную скорость называется импульсом (p¯). Теперь стоит ввести новую величину:

Вам будет интересно: Сульфат стронция: нахождение в природе, растворимость, применение

Здесь векторная величина L¯ представляет собой момент импульса. Чтобы перейти к скалярной форме записи, необходимо знать модули соответствующих значений r¯ и p¯, а также угол θ между ними. Скалярная формула для L имеет вид:

L = r*m*v*sin(θ) = r*p*sin(θ).

На рисунке выше угол θ является прямым, поэтому можно просто записать:

Из записанных выражений следует, что единицей измерения для L будут кг*м2/с.

Видео:Физика - импульс и закон сохранения импульсаСкачать

Направление вектора момента импульса

Поскольку рассматриваемая величина является вектором (результат векторного произведения), то она будет иметь определенное направление. Из свойств произведения двух векторов следует, что их результат даст третий вектор, перпендикулярный плоскости, образованной первыми двумя. При этом направлен он будет таким образом, что если смотреть с его конца, то тело будет вращаться против часовой стрелки.

Результат применения этого правила показан на рисунке в предыдущем пункте. Из него видно, что L¯ направлен вверх, поскольку, если смотреть на тело сверху, его движение будет происходить против хода стрелки часов. При решении задач важно учитывать направление во время перехода к скалярной форме записи. Так, рассмотренный момент импульса считается положительным. Если бы тело вращалось по часовой стрелке, тогда в скалярной формуле перед L следовало бы поставить знак минуса (-L).

Видео:Момент импульса. Закон сохранения момента импульса. Физика 10 классСкачать

Аналогия с линейным импульсом

Вам будет интересно: Самые старые горы в мире: где находятся, фото, названия

Рассматривая тему момента импульса и закона его сохранения, можно проделать один математический трюк — преобразовать выражение для L¯, помножив и поделив его на r2. Тогда получится:

L¯ = r*m*v¯*r2/r2 = m*r2*v¯/r.

В этом выражении отношение скорости к радиусу вращения называется угловой скоростью. Она обычно обозначается буквой греческого алфавита ω. Эта величина показывает, на сколько градусов (радиан) сделает поворот тело по орбите своего вращения за единицу времени. В свою очередь, произведение массы на квадрат радиуса — это тоже физическая величина, имеющая собственное название. Обозначают ее I и называют моментом инерции.

В итоге формула для момента импульса преобразуется в следующую форму записи:

L¯ = I *ω¯, где ω¯= v¯/r и I=m*r2.

Выражение демонстрирует, что направление момента импульса L¯ и угловой скорости ω¯ совпадают для системы, состоящей из вращающейся материальной точки. Особый интерес представляет величина I. Ниже она рассмотрена подробнее.

Видео:Физика - движение по окружностиСкачать

Момент инерции тела

Введенная величина I характеризует «сопротивляемость» тела любому изменению скорости его вращения. То есть она играет точно такую же роль, что и инерция тела при линейном перемещении объекта. По сути I для кругового движения с физической точки зрения означает то же самое, что и масса при линейном движении.

Как было показано, для материальной точки с массой m, вращающейся вокруг оси на расстоянии от нее r, момент инерции рассчитать просто (I = m*r2), однако для любых других тел этот расчет будет несколько сложным, поскольку предполагает использование интеграла.

Для тела произвольной формы I можно определить при помощи следующего выражения:

I = ∫m(r2*dm) = ∫V(r2*ρ*dV), где ρ — плотность материала.

Вам будет интересно: Архаический период Древней Греции (IX–VIII вв. до н.э.)

Выражения выше означают, что для вычисления момента инерции следует разбить все тело на бесконечно малые объемы dV, умножить их на квадрат расстояния до оси вращения и на плотность и просуммировать.

Для тел разной формы эта задача решена. Ниже приводятся данные для некоторых из них.

Материальная точка: I = m*r2.

Диск или цилиндр: I = 1/2*m*r2.

Стержень длиной l, закрепленный по центру: I = 1/12*m*l2.

Момент инерции зависит от распределенной массы тела относительно оси вращения: чем дальше от оси будет находиться большая часть массы, тем больше будет I для системы.

Видео:Момент импульсаСкачать

Изменение момента импульса во времени

Рассматривая момент импульса и закон сохранения момента импульса в физике, можно решить простую проблему: определить, как и за счет чего он будет изменяться во времени. Для этого следует взять производную по dt:

dL¯/dt = d(r¯*m*v¯)/dt = m*v¯*dr¯/dt+r*m*dv¯/dt.

Первое слагаемое здесь равно нулю, поскольку dr¯/dt = v¯ и произведение векторов v¯*v¯ = 0 (sin(0) = 0). Второе же слагаемое может быть переписано следующим образом:

dL¯/dt =r*m*a¯, где ускорение a = dv¯/dt, откуда:

Величина M¯, согласно определению, называется моментом силы. Она характеризует действие силы F¯ на материальную точку массой m, расположенную на расстоянии r от оси вращения.

Что показывает полученное выражение? Оно демонстрирует, что изменение момента импульса L¯ возможно только за счет действия момента силы M¯. Эта формула — закон сохранения момента импульса точки: если M¯=0, то dL¯/dt = 0 и L¯ является постоянной величиной.

Видео:Сохранение момента импульса при переменном моментеСкачать

Какие моменты сил могут изменить L¯ системы?

Существует два вида моментов сил M¯: внешние и внутренние. Первые связаны с силовым воздействием на элементы системы со стороны любых внешних сил, вторые же возникают за счет взаимодействия частей системы.

Согласно третьему закону Ньютона, любой силе действия соответствует направленная противоположно сила противодействия. Это означает, что суммарный момент силы любых взаимодействий внутри системы всегда равен нулю, то есть он не может повлиять на изменения момента импульса.

Величина L¯ может измениться только за счет внешних моментов сил.

Видео:Моменты силы, импульса, инерции. Динамика вращательного движенияСкачать

Формула закона сохранения момента импульса

Формула для записи выражения сохранения величины L¯ в случае, если сумма внешних моментов сил равна нулю, имеет следующий вид:

Любые изменения момента инерции системы пропорционально отражаются на изменении угловой скорости таким образом, что произведение I*ω не меняет своего значения.

Вид этого выражения аналогичен закону сохранения линейного импульса (роль массы играет I, а роль скорости — ω). Если развивать аналогию дальше, то, помимо этого выражения, можно записать еще одно, которое будет отражать сохранение кинетической энергии вращения:

E = I *(ω)2/2 = const.

Применение закона сохранения момента импульса находит себя в целом ряде процессов и явлений, которые кратко охарактеризованы ниже.

Видео:Физика 10 класс (Урок№4 - Равномерное движение точки по окружности.)Скачать

Примеры использования закона сохранения величины L¯

Следующие примеры закона сохранения момента импульса имеют важное значение для соответствующих сфер деятельности.

• Любой вид спорта, где необходимо совершать прыжки с вращением. Например, балерина или спортсмен по фигурному катанию начинает исполнение пируэта с вращением, разведя широко руки и отодвинув ногу от центра тяжести своего тела. Затем он прижимает ногу ближе к опорной и руки ближе к телу, уменьшая тем самым момент инерции (большая часть точек тела расположена близко к оси вращения). По закону сохранения величины L, должна увеличиться его угловая скорость вращения ω.

• Для изменения направления ориентации относительно Земли какого-либо искусственного спутника. Выполняется это так: спутник имеет специальный тяжелый «маховик», его приводит в движение электромотор. Общий момент импульса должен сохраняться, поэтому сам спутник начинает вращаться в противоположную сторону. Когда он примет нужную ориентацию в пространстве, маховик останавливают, и спутник также перестает вращаться.
• Эволюция звезд. По мере того как звезда сжигает свое водородное топливо, силы гравитации начинают преобладать над давлением ее плазмы. Этот факт приводит к уменьшению радиуса звезды до небольших размеров и, как следствие, к сильному увеличению скорости вращения угловой. Например, установлено, что нейтронные звезды, имеющие диаметр несколько километров, вращаются с гигантскими скоростями, делая один оборот за доли миллисекунды.

Видео:Импульс тела и импульс силы. Закон сохранения импульса. 10 класс.Скачать

Решение задачи на закон сохранения L¯

Учеными установлено, что через несколько миллиардов лет Солнце, исчерпав энергетические запасы, превратится в «белого карлика». Необходимо рассчитать, с какой скоростью оно будет вращаться вокруг оси.

Для начала необходимо выписать значения необходимых величин, которые можно взять из литературы. Итак, сейчас данная звезда имеет радиус 696 000 км и один оборот вокруг своей оси делает за 25,4 земных суток (значение для области экватора). Когда она подойдет к концу своего эволюционного пути, то сожмется до размеров 7000 км (порядка радиуса Земли).

Полагая, что Солнце — идеальный шар, можно воспользоваться формулой закона сохранения момента импульса для решения этой задачи. Нужно перевести сутки в секунды и километры в метры, получается:

L = I*ω = 2/5*m*r12*ω1 = 2/5*m*r22*ω2.

ω2 = (r1/r2)2*ω1 = (696000000/7000000)2*2*3,1416/(25,4*24*3600)= 0,0283 рад/с.

Здесь использовалась формула для угловой скорости (ω = 2*pi/T, где T — период вращения в секундах). При выполнении вычислений также было сделано предположение, что масса Солнца остается постоянной (это не верно, поскольку она будет уменьшаться. Тем не менее полученное значение ω2 является нижней границей, то есть в действительности Солнце-карлик будет вращаться еще быстрее).

Поскольку полный оборот — это 2*pi радиан, тогда получится:

T2 = 2*pi/ω2 = 222 с.

То есть в конце своего жизненного цикла данная звезда будет делать один оборот вокруг своей оси быстрее, чем за 222 секунды.

💥 Видео

Скамья Жуковского (закон сохранения момента импульса)Скачать

5.2. Момент импульса системы материальных точек | Динамика | Александр Чирцов | ЛекториумСкачать

Движение материальной точки по окружности | Физика ЕГЭ, ЦТСкачать

Консультация к устному экзамену. Механика. Часть 4: "Вращение твердых тел"Скачать

Равномерное движение точки по окружности | Физика 10 класс #7 | ИнфоурокСкачать

Урок 110. Следствия из закона сохранения момента импульсаСкачать

Вращательное движение. 10 класс.Скачать