Могут ли прямые а и б быть параллельными проекциями параллельных

Если прямые в пространстве параллельны, то их проекции также параллельны (рис. 5). Доказательство: прямые АВ и CD проецируются с помощью проецирующих плоскостей У и Т, но У¦Т, т. к. АВ¦CD по условию и ААN¦ССN — по построению. Известно, что если две параллельные плоскости пересекаются третьей, то образуются параллельные прямые. Здесь две параллельные плоскости У и Т пересекаются плоскостью проекций ПN и образуются параллельные прямые (АNВN¦CNDN).

Проекции геометрических фигур, параллельных плоскости проекций. Если данная геометрическая фигура — прямая, кривая линия или плоская фигура (треугольник, многоугольник, эллипс, окружность и т. п.) лежит в плоскости, параллельной плоскости проекций, то она проецируется на плоскость проекций в натуральную величину. Доказательство: дано У¦ПN и АВ У (рис. 6). Требуется доказать, что АВ¦АNВN и АВ=АNВN. Так как У¦ПN , то отрезки ААN и ВВN равны и параллельны. Следовательно, четырехугольник АВВNАN является параллелограммом и АВ¦АNВN, АВ=АNВN.

Так же доказывается теорема относительно любой плоской кривой и любой плоской фигуры.

— цилиндрические поверхности в параллельной системе проецирования и конические поверхности в центральной системе проецирования — проецируют пространственные кривые линии и пространственные фигуры.

Основное свойство проецирующей геометрической фигуры заключается в том, что точки, прямые или кривые линии, плоские и пространственные фигуры, расположенные на проецирующей геометрической фигуре, проецируются на линию пересечения этой фигуры с плоскостью проекций. Эта линия называется следом данной проецирующей геометрической фигуры или ее главной проекцией.

На рис. 7 показаны проецирующие геометрические фигуры в ортогональной системе проецирования: проецирующая прямая а, проецирующая плоскость У и проецирующая цилиндрическая поверхность Ф.

Прямая а, плоскость У и образующие цилиндрической поверхности Ф перпендикулярны плоскости проекций ПN . Их главные проекции аN , УN и ФN включают в себя проекции всех точек данной проецирующей геометрической фигуры.

Дополнения однокартинного чертежа. Ранее было показано, что одна проекция точки не определяет ее положения в пространстве.

Для того, чтобы чертеж был полным и обратимым, т.е. для того, чтобы по чертежу можно было представить положение точки в пространстве, применяются разные способы.

Способ числовых отметок. Около проекции точки ставится число, выражающее в некоторых линейных единицах расстояние данной точки от плоскости проекций.

На рис. 8 даны проекции различных геометрических фигур с числовыми отметками.

Около проекции точки А стоит цифра 20. Это означает, что точка А отстоит от плоскости проекций на расстоянии 20 линейных единиц.

Концы отрезка ВС отстоят от плоскости на расстояниях 15 и 30, вершины треугольника DEF — на расстояниях соответственно 0, 10 и 25.

Кривая поверхность задана кривыми линиями, принадлежащими поверхности и параллельными плоскости проекций (горизонталями, если плоскость ПN горизонтальна). Около каждой горизонтали стоит число, выражающее ее расстояние от плоскости ПN.

С помощью горизонталей изображается рельеф земной поверхности на топографических картах и сложные кривые поверхности, в том числе поверхности манекена и обувной колодки.

Проекции, полученные при центральном и параллельном проецировании, обладают рядом свойств.

Проекция точки есть точка. При заданном центре Р (.или направлении S) проецированию любой точки А пространства соответствует иа плоскости проекций п’ единственная точка А’. При этом проекция точки В, лежащей в плоскости проекций, совпадает с самой точкой (см. рис. 43).

Проекция прямой есть прямая. На рис. 46 лучи, проецирующие прямую т, создают плоскость S, которая пересекает плоскость проекций п’ по линии m’, являющейся проекцией на плоскость n’; S

т; S п п = т’. Проекция прямой определена, если известны проекции хотя бы двух ее точек (рис. 9). Если в пространстве прямая параллельна плоскости проекции п’, то ее проекция параллельна самой прямой (рис. 10). При этом при центральном проецировании проекции отрезков пропорциональны самим отрезкам, а при параллельном — равны им.

При параллельном проецировании сохраняется отношение величин отрезков прямой и их проекций (рис. 11):

При параллельном проецировании проекции параллельных прямых есть прямые параллельные (рис. 12). Если прямые т и п в пространстве параллельны, то и проецирующие их плоскости Sm и Sn тоже будут параллельны. При пересечении их с плоскостью проекций п’ получаем т’|| п’.

Проекцией плоскости является плоскость проекций. Плоскость состоит из бесконечного множества точек. При проецировании этого множества проецирующие лучи заполняют все пространство, а их точки пересечения с плоскостью проекций п’ — всю плоскость проекций.

Так как положение любой плоскости в пространстве определяется тремя ее точками, не лежащими на одной прямой, то проекция трех таких точек плоскости (рис. 13, а) устанавливает однозначное соответствие между проецирующей плоскостью и плоскостью проекций n’, которое позволяет определить проекции (рис. 13, б) любой точки D или прямой этой плоскости.

Если плоскость параллельна плоскости проекций, то проекции ее плоских фигур при центральном проецировании подобны самим фигурам (рис. 14, а), а при параллельном — равны им (рис. 14,6).

Если плоскость угла параллельна плоскости проекций, величина проекции угла и при центральном, и при параллельном проецировании равна натуральной величине. На рис. 54, a угол ABC = уголA’B’C’, так как АВС бесконечность А’В’С’, а на рис. 54, б угол ABC = углу А’В’С’, так как АВС = А’В’С’.

При параллельном проецировании проекции фигуры не изменяется при параллельном переносе плоскости j проекций (рис. 15).

Прямые и плоскости (поверхности) могут занимать в пространстве проецирующее положение, если с ними совпадают проецирующие лучи. При центральном проецировании это прямые и плоскости, проходящие через центр проекций, пирамидальные и конические поверхности, у которых вершины совпадают с центром проецирования (рис. 56). При параллельном проецировании — это прямые и плоскости, параллельные направлению проецирования, призматические и цилиндрические поверхности, ребра и образующие которых параллельны направлению проецирования (рис. 57).

Все эти геометрические фигуры можно рассматривать состоящими из проецирующих лучей, каждый из которых изображается точкой. Отсюда следует, что проекциями прямых, плоскостей, поверхностей, занимающих проецирующее положение, есть точки или линии их пересечения с плоскостью проекций («вырожденные» проекции).

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

1. Прямые a и b лежат в параллельных плоскостях α и β?

Геометрия | 10 — 11 классы

1. Прямые a и b лежат в параллельных плоскостях α и β.

Могут ли эти прямые быть : а) параллельными ; б) скрещивающимися?

Сделайте рисунок для каждого возможного случая.

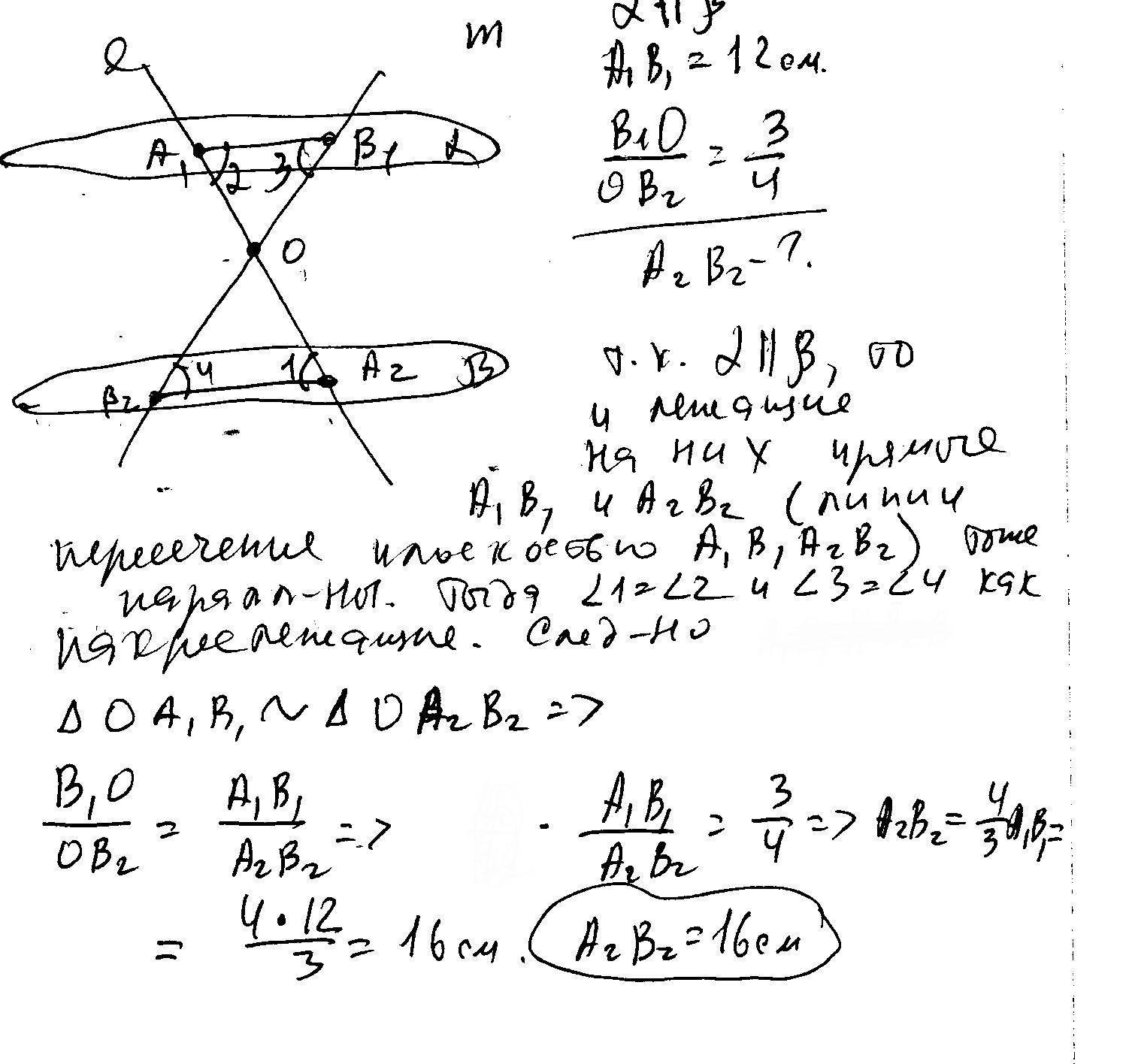
2. Через точку О, лежащую между параллельными плоскостями α и β, проведены прямые l и m.

Прямая l пересекает плоскости α и β в точках А1 и А2 соответственно, прямая m – в точках В1 и В2.

Найдите длину отрезка А2В2, если А1В1 = 12 см, В1О : ОВ2 = 3 : 4.

1. Прямые a и b лежат в параллельных плоскостях α и β.

Могут ли эти прямые

быть : а) параллельными ; б) скрещивающимися?

Сделайте рисунок для

каждого возможного случая.

2. Через точку О, лежащую между параллельными плоскостями α и β,

проведены прямые l и m.

Прямая l пересекает плоскости α и β в точках А1 и

А2 соответственно, прямая m – в точках В1 и В2.

Найдите длину отрезка

А2В2, если А1В1 = 12 см, В1О : ОВ2 = 3 : 4.

Видео:№16. Параллельные прямые a и b лежат в плоскости α. Докажите,Скачать

1) Всегда ли две не пересекающиеся1) Всегда ли две не пересекающиеся прямые в пространстве параллельны?

1) Всегда ли две не пересекающиеся1) Всегда ли две не пересекающиеся прямые в пространстве параллельны?

2) прямая a скрещивается с прямой b , а прямая b скрещивается с прямой c.

Следует ли отсюда , что прямые a и c скрещиваются?

3)укажите случаи взаимного расположения прямой и плоскости?

4)Даны параллельные прямая и плоскость.

Сколько можно провести в этой плоскости прямых, параллельных данной прямой?

5)прямые a и b параллельны.

Какое положение может занимать прямая aотносительно плоскости, проходящей через прямую b?

6)даны две параллельные прямые.

Через каждую из них проведена плоскость .

Эти две плоскости пересекаются .

Как расположена их линия пересечения относительно данных прямых?

7) через каждую из двух параллельных прямых проведена плоскость .

Можно ли утверждать, что эти плоскости параллельны?

8)могут ли быть параллельными две плоскости , проходящие через не параллельные прямые ?

9)Плоскость α пересекает плоскости β и γ по параллельным прямым.

Будут ли плоскости β и γ параллельны?

10)даны две параллельные плоскости α и β.

Через прямую a плоскости α и точку Aплоскости β проведите мысленно плоскость γ.

Какова взаимное расположение прямой a и линии пересечения плоскостей γ и β?

11)В каком случае параллельной проекций прямой будет точка?

Видео:Параллельность прямой и плоскости. 10 класс.Скачать

Прямые a и b лежат в пересекающихся плоскостях α и β?

Прямые a и b лежат в пересекающихся плоскостях α и β.

Могут ли эти прямые быть : а) параллельными ; б) скрещивающимися?

Сделайте рисунок для каждого возможного случая.

Видео:Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

Прямые а и в пересекающихся плоскостях альфа и бетта?

Прямые а и в пересекающихся плоскостях альфа и бетта.

Могут ли эти прямые быть — параллельными — скрещивающимися сделать рисунок.

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

1. Прямые а и в лежат в параллельных плоскостях альфа и бетта?

1. Прямые а и в лежат в параллельных плоскостях альфа и бетта.

Могут ли эти прямые быть : а)параллельными.

Сделайте рисунок для каждого возможного случая.

2. Через точку О, лежащую между параллельными плоскостями альфа и бетта, проведены прямые l и m.

Прямая l пересекает плоскости альфа и бетта в точках А1 и А2 соответсвенно прямая m — в точках В1 и В2.

Найдите длину отрезка А2В2, А1В1 = 12см, В1О : ОВ2 = 3 : 4.

3. Изобразите параллелепипед АВСДА1В1С1Д1 и постройте его сечение плоскостью , проходящей через точки М, N и К, являющиеся серединами ребер АВ, ВС и ДД1.

Видео:Параллельные прямые. 6 класс.Скачать

Прямые a и b лежат в параллельных плоскостях α и β?

Прямые a и b лежат в параллельных плоскостях α и β.

Могут ли эти прямые быть : а) параллельными ; б) скрещивающимися?

Сделайте рисунок для каждого возможного случая.

Видео:Параллельность прямой к плоскостиСкачать

Прямые a и b лежат в пересекающихся плоскостях α и β?

Прямые a и b лежат в пересекающихся плоскостях α и β.

Могут ли эти прямые быть : а) параллельными ; б) скрещивающимися?

Сделайте рисунок для каждого возможного случая.

Видео:Геометрия 7 класс (Урок№18 - Параллельные прямые.)Скачать

Прямые a и b лежат в пересекающихся плоскостях α и β?

Прямые a и b лежат в пересекающихся плоскостях α и β.

Могут ли эти прямые быть : а) параллельными ; б) скрещивающимися?

Сделайте рисунок для каждого возможного случая.

Видео:10 класс, 5 урок, Параллельность трех прямыхСкачать

1. Прямые a и b лежат в пересекающихся плоскостях ?

1. Прямые a и b лежат в пересекающихся плоскостях ?

И . Могут ли эти прямые быть : а) параллельными ; б) скрещивающимися?

Сделайте рисунок для каждого возможного случая.

Видео:10 класс, 7 урок, Скрещивающиеся прямыеСкачать

Прямые a и b лежать в параллельных плоскостях альфа и бета?

Прямые a и b лежать в параллельных плоскостях альфа и бета.

Могут ли эти прямые быть параллельными ; скрещивающимися?

Сделайте рисунок для каждого возможного случая.

Видео:Параллельные прямые (задачи).Скачать

Прямые a и b лежат в параллельных плоскостях?

Прямые a и b лежат в параллельных плоскостях.

Могут ли эти прямые быть : а)параллельными ; б)скрещивающимися?

Вы зашли на страницу вопроса 1. Прямые a и b лежат в параллельных плоскостях α и β?, который относится к категории Геометрия. По уровню сложности вопрос соответствует учебной программе для учащихся 10 — 11 классов. В этой же категории вы найдете ответ и на другие, похожие вопросы по теме, найти который можно с помощью автоматической системы «умный поиск». Интересную информацию можно найти в комментариях-ответах пользователей, с которыми есть обратная связь для обсуждения темы. Если предложенные варианты ответов не удовлетворяют, создайте свой вариант запроса в верхней строке.

Средняя линия треугольника соединяет середины двух сторон и равна половине третьей стороны, таким образом : DF — средняя линия ΔAOC и AC = 2DF. DE — средняя линия ΔAOB и AB = 2DE. EF — средняя линия ΔBOC и BC = 2EF. ΔABC

ΔDFE по трём сторонам (они..

Осевое сечение цилиндра — квадрат т. Е 2R = 5 R = 2. 5 H = 5 S(полн) = 2πR² + 2πRH = 12. 5π + 25π = 37. 5π.

3400мм + 24мм + 1600мм + 93мм = 5117мм = 51 дм 17мм.

Вот если пригодиться).

Решение смотри на фото.

1)14х2 = 28 см(катет, лежащий напротив угла в 30 градусов равен половине гипотенузы).

28 так как сторона AC лежит напротив угла B = 30 град.

Если внешний 130, внутренний у основания будет 180 — 130 = 50 (смежные углы) значит второй у основания тоже 50, тк равнобедренный треугольник. Угол при вершине будет 180 — 50 — 50 = 80 (сумма всех углов любого треугольника 180) Ответ : 80 ; 50 ; 50.

Видео:Следы прямой Взаимное положение двух прямыхСкачать

Школьная лекция по теме «Параллельность в пространстве» 10 класс

Видео:№91. Через каждую из двух параллельных прямых a и b и точку М, не лежащую в плоскости этих прямыхСкачать

«Календарь счастливой жизни:
инструменты и механизм работы
для достижения своих целей»

Сертификат и скидка на обучение каждому участнику

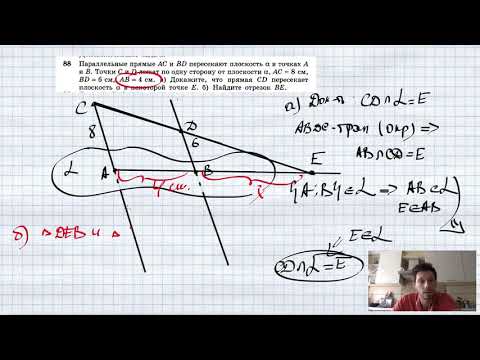
Видео:№88. Параллельные прямые АС и BD пересекают плоскость α соответственно в точках А и В. Точки С и DСкачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

Тема: «Параллельность в пространстве» Урок-лекция 10 класс

Основные определения: две прямые в пространстве параллельны, если они лежат в одной плоскости и не пересекаются. две плоскости называются параллельными, если они не пересекаются. плоскость и прямая называются параллельными, если они не пересекаются.

Теоремы-признаки Две прямые параллельны между собой, если они каждая параллельны третьей прямой. Если прямая, не принадлежащая плоскости параллельна какой-либо прямой в этой плоскости, то она параллельна самой плоскости. Если две пересекающихся прямых одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то плоскости параллельны между собой.

Теорема –признак параллельности прямой и плоскости. Если прямая, не лежащая в плоскости , параллельна какой-то прямой в плоскости, то она параллельна всей плоскости. Доказательство: Пусть есть прямая а в плоскости α , а вне её есть прямая в, причём а//в. Докажем , что в//α. Пусть не параллельна, тогда прямая в пересекает плоскость в некоторой точке С. Так как через две пересекающиеся прямые проходит плоскость β, то плоскость α имеет с плоскостью β общую точку С, а значит пересекается по прямой а. Тогда через точку С проходят две различные прямые, которые по предположению пересекаются, а по условию параллельны. Этого быть не может, значит, предположение не верно, и прямая а//α.

Теорема-признак параллельности плоскостей Если две пересекающихся прямых одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то плоскости параллельны между собой. Пусть плоскости пересекаются. Тогда прямая с принадлежит и плоскости α и плоскости β. Получается, что если сα, то с//а и с//в, лежащих в плоскости β , так как если прямая параллельна плоскости, тогда она параллельна любой прямой этой плоскости. Значит, через точку С проходит две различные параллельные прямые. Что является противоречием, а значит плоскость α параллельна плоскости β.

Теоремы (для построения) Через точку вне прямой можно провести прямую параллельную данной и только одну. Через точку вне плоскости можно провести плоскость параллельную данной и только одну. Если две параллельные плоскости пересечены третьей, то прямые пересечения параллельны. Отрезки параллельных прямых, заключённые между двумя параллельными прямыми равны между собой .

Изображение пространственных фигур. Свойство 1. Если прямая параллельна или совпадает с прямой l, то ее проек­цией в направлении этой прямой является точка. Если прямая не парал­лельна и не совпадает с прямой l, то ее проекцией является прямая. Свойство 2. Проекция отрезка при параллельном проектировании есть точка или отрезок, в зависимости от того лежит он на прямой, параллельной или совпадающей с прямой l, или нет. Параллельное проектирование сохраняет отношение длин отрезков, лежащих на прямой, не параллельной и не совпадающей с прямой l. В частности, при парал­лельном проектировании середина отрезка переходит в середину соответствующего отрезка. Свойство 3. Если две параллельные прямые не параллельны прямой l, то их проекции в направлении l могут быть или параллельными прямыми или од­ной прямой. Свойство 4. Если плоская фигура F лежит в плоскости, параллель­ной плоскости проектирования π, то ее проекция F’ на эту плоскость бу­дет равна фигуре F. Пусть F — некоторая фигура в пространстве. Проекции ее точек на плоскость α образуют фигуру F ‘, которая называется параллельной проек­цией фигуры Ф на плоскость α в направлении прямой l. Говорят также, что фигура F ‘ получена из фигуры F параллельным проектированием.

Основное правило: параллельность и отношение длин сохраняется, длины отрезков и углы, не сохраняются . на основании этого правила скажите квадрат изображается? прямоугольник изображается? параллелограмм изображается? медиана изображается? высота изображается? Круг изображается овалом или эллипсом .

Из свойств параллельного проектирования следует, что параллельной проекцией многоугольника является или многоугольник с тем же числом сторон или отрезок. Причем, если в многоугольнике какие-нибудь две стороны параллельны, то их проекции также будут параллельны. При параллельном проектировании длины отрезков и углы, не сохраняются, проекцией равностороннего треугольника может быть треугольник с разной длиной сторон, проекцией прямоугольно­го треугольника может быть не прямоугольный треугольник. Проекцией параллелограмма является параллелограмм, проекцией пря­моугольника может не быть прямоугольник, проекцией ромба не обязательно является ромб, проекцией правильного многоугольника может быть неправильный многоугольник.

Изображение параллелепипеда строится, исходя из того, что все его грани параллелограммы и, следовательно, изображаются параллелограмма­ми параллелепипед куб Прямоугольный параллелепипед

Для того чтобы построить изображение призмы, достаточно постро­ить многоугольник, изображающий ее основание. Затем из вершин многоу­гольника провести прямые, параллельные некоторой фиксированной прямой, и отложить на них равные отрезки. Соединяя концы этих отрезков, полу­чим многоугольник, являющийся изображением второго основания призмы

Для того чтобы построить изображение пирамиды, достаточно пост­роить многоугольник, изображающий ее основание. Затем выбрать ка­кую-нибудь точку, которая будет изображать вершину пирамиды, и соеди­нить ее с вершинами многоугольника. Полученные отрезки бу­дут изображать боковые ребра пирамиды.

Упражнения 1. В каком случае параллельной проекцией прямой будет точка? Ответ: Если прямая параллельна направлению проектирования. 2. В каком случае параллельной проекцией двух параллельных прямых является одна прямая? Ответ: Если плоскость, в которой лежат эти прямые, параллельна направлению проектирования. 3. Какие фигуры могут быть параллельными проекциями двух скре­щивающихся прямых? Ответ: Две пересекающиеся прямые; две параллельные прямые; прямая и точка, ей не принадлежащая. 4. Сохраняются ли при параллельном проектировании: а) длины отрезков; б) величины уг­лов? Ответ: а), б) Нет.

5. Верно ли, что если длина отрезка равна длине его параллельной проекции, то отрезок параллелен плоскости проектирования? Ответ: Нет. 6. Может ли параллельной проекцией равностороннего треугольника быть: а) прямоугольный треугольник; б) равнобедренный треугольник; в) разносторонний треугольник? Ответ: а), б), в) Да. 7. Может ли параллельной проекцией прямоугольника быть: а) квадрат; б) параллелограмм; в) ромб; г) трапеция? Ответ: а), б), в) Да; г) нет. 8. Верно ли, что при параллельном проектировании треугольника: а) медианы проектируются в медианы; б) высоты проектируются в высоты; в) биссектрисы проектируются в биссектрисы? Ответ: а) Да; б), в) нет.

Параллельными проекциями каких многогранников являются фигуры, изображенные на рисунке? Ответ: а), б) 4-я пирамида; в) тетраэдр; г), д) 6-я пирамида; е) параллелепипед.

Верно ли? Для любых двух прямых можно провести плоскость, параллельную каждой из них.(нет, случай перпендикулярности прямых). Все прямые , проходящие через данную точку, параллельно данной плоскости, лежат в одной плоскости.(да). Сохраняется ли при параллельном проектировании отрезков одной плоскости их отношение?(да) Может ли при параллельном проектировании трапеции получиться прямоугольник? (нет). Может ли при параллельном проектировании параллелограмма получиться прямоугольник?(да) Может ли параллельная проекция произвольного параллелограмма быть ромбом? (нет) Если прямая параллельна плоскости, то она параллельна любой прямой, лежащей в плоскости? (нет)

Какая из указанных фигур не может быть параллельной проекцией правильного треугольника, в котором построена одна высота?

Какая из указанных фигур не может быть проекцией пространственного четырёхугольника?

Каково взаимное расположение а и в?АДα. ВС по отношению к α?

АДα..МNпо отношению к ВС?

В пространстве даны прямая и точка А. Сколько существует прямых, которые проходят через А и параллельны прямой. Через стороны АВ и СД четырёхугольника АВСД и точку К вне его проведены две плоскости , пересекающиеся по прямой параллельной каждой из прямых АВ иСД. Установите вид четырёхугольника АВСД, если известно, что АВ=СД.

С А В F N M К Дано: F ∉ АВС. FА, FВ, FС. АМ=MF, BK=FK, FN=NC. Выбрать три пары параллельных прямых. Доказать, что они параллельны.

С А В F N M К Дано:∆ АВС, F ∉ (АВС) M∈AF, K∈FB, N∈FC FM:MF=FK:KB=FN:NC Доказать, что (ABC)||(MNK)

В С С₁ В₁ А α Дано :α ∩ AB=B₁; α ∩ AC=C₁ AB₁:B₁C₁=2:3, BC=15 см, ВВ₁=6 см BC||α Найти: В₁С₁

α M N A B C D Дано : АВСD- трапеция α││АD; α∩АВ=М ,α∩ СД=N AM=MB, CN=ND. BC=9 см , AD= 17см Найти :MN

Отрезок АВ не пересекает плоскость α. Через середину отрезка С и концы отрезка А и В проведены прямые, параллельные между собой и пересекающие плоскость α в точках А1 , В1 и С1. Вычислить длину отрезка СС1, если АА1= 5, ВВ1= 7. α А В С А1 В1 С1

📽️ Видео

Параллельность прямых и плоскостей в пространстве. Практическая часть - решение задачи. 10 класс.Скачать

Лекция 1. Классификация прямых линий.Скачать

10 класс, 4 урок, Параллельные прямые в пространствеСкачать

Взаимное расположение прямых в пространстве. 10 класс.Скачать

Параллельная проекцияСкачать

Параллельное проектирование и его свойстваСкачать