Методом параллельного переноса определите точку пересечения отрезка прямой с заданной плоскостью

Способ плоскопараллельного перемещения (переноса) имеет справедливым утверждение, которое может быть выражено в виде следующей теоремы.

При параллельном переносе геометрической фигуры относительно плоскости проекции, проекция фигуры на эту плоскость хотя и меняет свое положение, но остается конгруентной проекции фигуры в ее исходном положении.

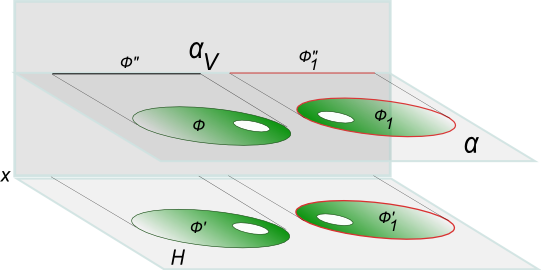
Докажем эту теорему для случая, когда проецируемая фигура Ф плоская, и ее плоскость принадлежит плоскости уровня Ф⊂α, плоскость α║H (рисунок). В этом случае, на основании свойства 6 ортогонального проецирования горизонтальная проекция Ф` будет конгруентна самой фигуре Ф(Ф`≅Ф).

При перемещении фигуры Ф в новое положение Ф₁, фигура Ф`₁ будет конгруентна Ф, так как:

а) расстояние между точками фигуры не меняется;

б) в процессе перемещения фигура Ф все время остается в плоскости α.

В силу параллельности плоскостей α и H, Ф`<sub>1</sub>≅Ф<sub>1</sub>, но Ф<sub>1</sub>≅Ф, а Ф≅Ф`, следовательно Ф`<sub>1</sub>≅Ф`. Данная теорема будет справедлива и в случае, когда геометрическая фигура занимает произвольное (непараллельное) положение относительно плоскости проекции.

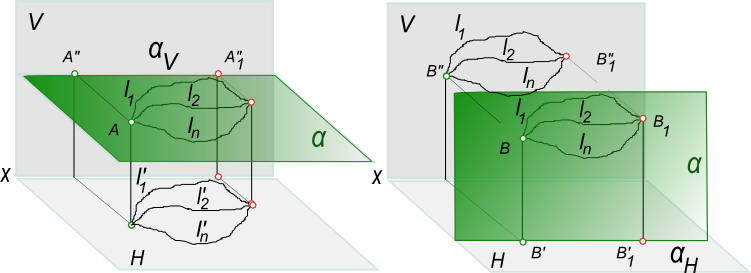
а) При всяком перемещении точки в плоскости, параллельной плоскости проекции H, ее фронтальная проекция перемещается по прямой, параллельной оси x.

б) В случае произвольного перемещения точки в плоскости, параллельной V, ее горизонтальная проекция перемещается по прямой, параллельной оси x.

Пользуясь теоремой и отмеченными свойствами, не составляет труда построить новые проекции геометрической фигуры (по заданным ее ортогональным проекциям), которые соответствуют частным положениям проецируемой фигуры по отношению к плоскости проекции.

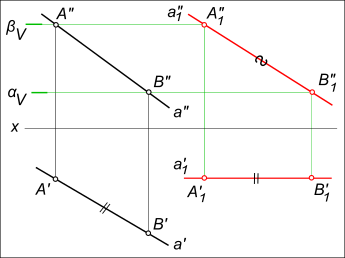
[AB]- отрезок прямой а общего положения перевести в положение параллельное V. Выполняем перемещение отрезка [A`B`] на горизонтальной плоскости проекции в положение параллельное оси x [A₁B₁]. При таком перемещении новая горизонтальная проекция конгруентна исходной [AB]≅[A₁B₁] на основании теоремы.

Фронтальные проекции точек отрезка [A»B»] будут перемещаться в новое положение [A»₁B»₁] в плоскостях α и β параллельных горизонтальной плоскости проекции — по следам α_V и β_V.

Для перевода отрезка прямой общего положения в положение параллельное V требуется одно перемещение отрезка параллельно плоскости проекции H.

Для перевода отрезка прямой из общего положения в проецирующее, необходимо последовательно выполнить два перемещения параллельно плоскостям проекции.

Зная характер геометрических построений, которые необходимо выполнить для перемещения отрезка из общего положения в проецирующее, можно легко перевести плоскость, произвольно расположенную в пространстве, в частное положение (параллельное или перпендикулярное плоскости проекции).

В графической работе №4 используется способ плоскопараллельного перемещения для решение задачи по построению треугольной пирамиды SABC: Графическая работа 4. В графической работе №5 используется способ плоскопараллельного перемещения для решение задачи по по определению наклона ребра SC треугольной пирамиды SABC к плоскости основания ABC: Графическая работа 5. Плоскопараллельное перемещение треугольника, со всеми подробностями, смотри: Плоскопараллельное перемещение треугольника

Видео:Точка встречи прямой с плоскостьюСкачать

Способ плоскопараллельного перемещения

В учебной литературе этот способ часто трактуется как поочередное вращение заданных фигур относительно проецирующих осей, но без указания положения последних на используемом чертеже.

Важно учесть, что при вращении фигуры вокруг оси, перпендикулярной к одной плоскости проекций, ее проекция на эту плоскость не меняется ни по виду, ни по величине (не претерпевает деформаций), а лишь меняет свое положение относительно оси проекций. Последнее обстоятельство дает возможность перемещать недефор- мированную проекцию объекта по одной из плоскостей так, как требует алгоритм решения. Что касается другой проекции объекта, располагающейся на плоскости, параллельной виртуальной (возможной) оси вращения, эта проекция хотя и претерпевает определенные деформации по форме и величине, однако все ее точки перемещаются в процессе преобразования на чертеже по прямым, параллельным оси проекций эпюра.

Использование способа плоскопараллельного перемещения обогащает арсенал средств нахождения истинной величины плоской фигуры общего положения.

Пусть задан треугольник общего положения АВС с горизонталью AD (рис. 50). На основании предложенной методики в качестве первого шага вращаем заданный треугольник АВС вокруг горизонталь- но-проецирующей оси, для чего меняем положения недеформиро- ванной горизонтальной проекции треугольника на эпюре таким образом, чтобы горизонтальная проекция горизонтали AD оказалась перпендикулярной оси проекций (нетрудно узнать в этом алгоритме закодированную операцию 2).

Если горизонтальная проекция отсека перемещена в новое положение без деформации, то другая проекция фигуры обязана «выродиться» в отрезок прямой (след проецирующей плоскости). Точки этой другой проекции находим, проводя из точек исходной фронтальной проекции треугольника прямые, параллельные оси проекций, до их пересечения с одноименными линиями проекционной связи, восставленными из горизонтальных проекций точек перемещенной фигуры.

Вторым шагом осуществляют вращение перемещенной в первом шаге фигуры вокруг фронтально проецирующей оси, для чего перемещают недеформированную фронтальную проекцию отсека (в виде следа) в положение, параллельное оси проекций (нетрудно узнать в этом алгоритме закодированную операцию 3), а все точки горизонтальной проекции переносят по прямым, параллельным оси. В местах пересечения линий проекционной связи, опущенных из полученных фронтальных проекций вершин треугольника, с одноименными горизонтальными траекториями горизонтальных проекций вершин фиксируют точки, определяющие искомую истинную величину фигуры треугольника ЛВС.

В заключение следует указать, что в дальнейшем нет больше нужды обращаться к исследованию решений задач на отыскание истинной величины плоской фигуры. Выше уже рассмотрены по крайней мере три варианта таких решений:

• 1) использование способа замены плоскостей проекций (с реализацией операций 2 и 3);
• 2) использование способа вращения плоской фигуры вокруг ее линии уровня (горизонтали или фронтали);
• 3) использование способа плоско-параллельного перемещения плоской фигуры.

Если заданная плоская фигура представляет собой многоугольник, ее разбивают с помощью диагоналей на ряд составляющих треугольников, истинную величину каждого из которых отыскивают порознь.

В примитивной форме задача на отыскание истинной величины треугольной фигуры может быть решена с помощью поочередного отыскания истинной величины каждой из сторон рассматриваемого треугольника. Затем на одной из сторон как на основании из концевых точек отрезка (двух вершин треугольника) делают засечки дугами, величины радиусов которых равны длинам двух других сторон фигуры. Пересечение дуг фиксирует третью вершину искомой фигуры.

Видео:Пересечение прямой и плоскостиСкачать

Метод плоскопараллельного перемещения

В начертательной геометрии метод плоскопараллельного перемещения используется, как правило, для определения натуральных величин плоских фигур, отрезков и углов.

Свойства плоскопараллельного перемещения:

1. При перемещении любой фигуры параллельно плоскости проекции, проекция фигуры на эту плоскость остается неизменной.
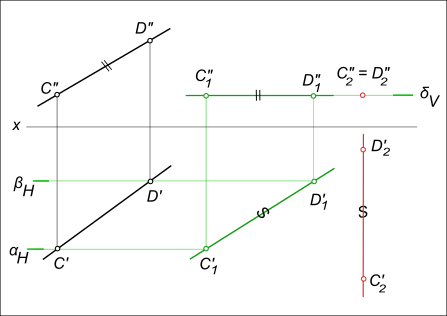
2. При перемещении точки параллельно горизонтальной плоскости проекции, её фронтальная проекция движется по прямой, параллельной оси X. На рисунке ниже точки C» и D», следуя этому свойству, заняли положение C»₁ и D»₁.
3. При перемещении точки параллельно фронтальной плоскости проекции, её горизонтальная проекция движется по прямой, параллельной оси X.

Рассмотрим перевод произвольно расположенного отрезка CD в положение, параллельное горизонтальной плоскости проекций П₂.

• Используя первое свойство параллельного перемещения, на любом свободном месте чертежа строим отрезок C’₁D’₁ = C’D’.
• По линиям связи определяем недостающие проекции C»₁ и D»₁. Стрелками показано перемещение точек C» и D» параллельно оси X в соответствии со вторым свойством рассматриваемого метода.

Следующий рисунок иллюстрирует перевод отрезка MN в проецирующее положение по отношению к фронтальной плоскости проекций П₂. В общем случае для решения подобной задачи необходимо дважды воспользоваться методом плоскопараллельного перемещения.

• После первого преобразования отрезок MN займет положение параллельно плоскости П₁. Сначала строится M»₁N»₁ = M»N» на произвольном месте чертежа, после чего по линиям связи находятся недостающие проекции M’₁ и N’₁.
• Второе преобразование заключается в параллельном переносе горизонтальной проекции отрезка M’₁N’₁ в положение M’₂N’₂, перпендикулярное оси X. После этого точки M»₂ = N»₂ определяются по линиям связи.

Видео:Пересечение прямой с плоскостью общего положения. Определение видимости методом конкурирующих точекСкачать

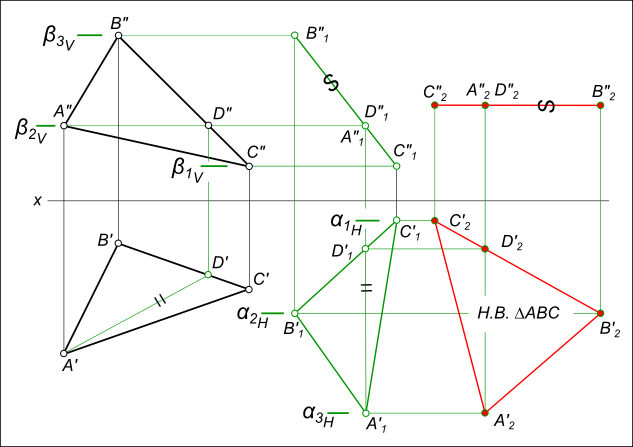
Определение натуральной величины треугольника

Рассмотрим порядок плоскопараллельного перемещения треугольника ABC с целью определения его натуральной величины.

1. Через точку С треугольника ABC проводим горизонталь CD. Находим её недостающие проекции.
2. Переводим ABC в положение, перпендикулярное фронтальной плоскости проекций. Для этого строим C’₁D’₁ = C’D’ перпендикулярно оси X. В соответствии с первым свойством плоскопараллельного перемещения достраиваем треугольник A’₁B’₁C’₁ = A’B’C’. По линиям связи определяем точки A»₁, B»₁, C»₁.
3. Перемещаем проекцию A»₁B»₁C»₁ треугольника ABC в положение A»₂B»₂C»₂, параллельное оси X, соблюдая равенство A»₂B»₂C»₂ = A»₁B»₁C»₁. По линиям связи определяем точки A’₂, B’₂, C’₂. Теперь треугольник ABC расположен параллельно горизонтальной плоскости проекций и проецируется на неё в натуральную величину A’₂B’₂C’₂.

Видео:Определение истинной величины треугольника АВС. Метод плоско-параллельного перемещенияСкачать

Определение расстояния между параллельными прямыми

Расстояние между двумя параллельными прямыми равно длине перпендикуляра, опущенного из произвольной точки первой прямой на вторую прямую. Рассмотрим, как указанное расстояние определяется на практике с помощью метода плоскопараллельного перемещения.

Путем двух последовательных преобразований прямые a и b переводятся в положение, перпендикулярное горизонтальной плоскости. Таким образом, они проецируются на неё в точки A’₂ и B’₂, расстояние между которыми является искомым. Показанные на рисунке величины d₁ и d₂ являются вспомогательными для выполнения построений согласно свойствам плоскопараллельного перемещения.

🌟 Видео

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Определение кратчайшей расстоянии от точки до плоскостиСкачать

Построение точки пересечения прямой с плоскостью, заданной следамиСкачать

Лекция 2. Основная задача начертательной геометрии. Точка пересечения прямой с плоскостью.Скачать

Пересечение двух плоскостей. Плоскости в виде треугольникаСкачать

Способ замены (перемены) плоскостей проекции. Определение истинной величины отрезка и плоской фигурыСкачать

Нахождение точки пересечения прямой и треугольникаСкачать

Построение линии пересечения поверхности конуса с проецирующей плоскостьюСкачать

Взаимно перпендикулярные плоскости. Определение кратчайшей расстоянии от точки до прямойСкачать

Точки пересечения прямой с поверхностью/Points of intersection of a straight line with a surface.Скачать

Построение параллельной плоскости на расстояние 30 мм.Скачать

Линия пересечения двух поверхностей вращения (Метод вспомогательных сфер)Скачать

Построение линии пересечения поверхности пирамиды с проецирующей плоскостьюСкачать

Построение следов плоскостиСкачать

Определение кратчайшей расстояние от точки до плоскости способом замены плоскостей проекцииСкачать

Нахождение истинной формы плоской фигуры методом плоско параллельного перемещенияСкачать