Метод левых треугольников интеграл (3 видео)

Численное интегрирование

Вычисляет определенный интеграл методом прямоугольников, трапеций или парабол (методом Симпсона).

Численные методы вычисления значения определенного интеграла применяются в том случае, когда первообразная подинтегральной функции не выражается через аналитические функции, и поэтому невозможно вычислить значение по формуле Ньютона-Лейбница. Для получения значения определенного интеграла таких функций можно воспользоваться численным интегрированием.

Численное интегрирование сводится к вычислению площади криволинейной трапеции, ограниченной графиком заданной функции, осью х и вертикальными прямыми ограничивающими отрезок слева и справа. Подинтегральная функция заменяется на более простую, обеспечивающую заданную точность, вычисление интеграла для которой не составляет труда.

Калькулятор ниже вычисляет значение одномерного определенного интеграла численно на заданном отрезке, используя формулы Ньютона-Котеса, частными случаями которых являются:

Содержание

Интеграл численным методом по формулам Ньютона-Котеса
Численное интегрирование с использованием функций Ньютона Котеса
Границы отрезка интегрирования
Погрешность вычисления
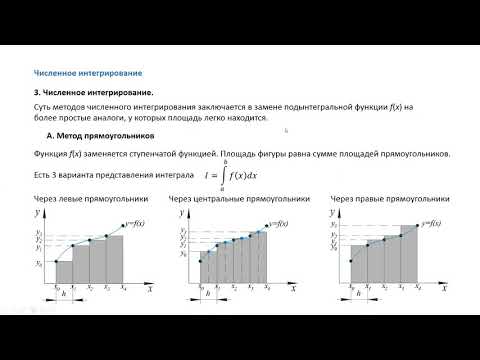
Метод прямоугольников
Суть метода прямоугольников
Метод средних прямоугольников
Оценка абсолютной погрешности метода средних прямоугольников
Метод левых прямоугольников и метод правых прямоугольников
Примеры применения метода прямоугольников при приближенном вычислении определенных интегралов
Замечание
Итоги
Метод левых треугольников интеграл
💡 Видео

Интеграл численным методом по формулам Ньютона-Котеса

Численное интегрирование с использованием функций Ньютона Котеса

При использовании функций Ньютона-Котеса отрезок интегрирования разбивается на несколько равных отрезков точками x₁,x₂,x₃..x_n.
Подинтегральную функцию заменяют интерполяционным многочленом Лагранжа различной степени, интегрируя который, получают формулу численного интегрирования различного порядка точности.

В итоге, приближенное значение определенного интеграла вычисляется, как сумма значений подинтегральной функции в узлах, помноженных на некоторые константы W_i (веса):

R_n — остаток или погрешность.
n — общее количество точек.
Сумма в формуле — квадратурное правило (метод).

В справочнике Квадратурные функции Ньютона-Котеса, мы собрали наиболее часто встречающиеся квадратурные правила, для интегрирования по равным отрезкам. Зарегистрированные пользователи могут добавлять в этот справочник новые правила.

Видео:Метод прямоугольников для нахождения определенного интегралаСкачать

Границы отрезка интегрирования

В зависимости от того, входят ли граничные точки отрезка в расчет, выделяют замкнутые и открытые квадратурные правила.

Открытые правила, (правила, в которых граничные точки не включаются в расчет) удобно использовать в том случае, если подинтегральная функция не определена в некоторых точках.
Например, используя метод прямоугольников мы сможем вычислим приблизительное значение интеграла функции ln(x) на отрезке (0,1), несмотря на то, что ln(0) не существует.

Замкнутые правила, напротив, используют значения функции в граничных точках для вычислений интеграла, ровно так же как и в остальных узлах.

Можно придумать правила, которые открыты только с одной стороны. Простейшим случаем таких правил являются правила левых и правых прямоугольников.

Видео:Численное интегрирование: Методы Левых Правых прямоугольников, Трапеций, Симпсона c++Скачать

Погрешность вычисления

В целом с увеличением количества узлов в правиле (при повышении степени интерполирующего полинома) возрастает точность вычисления интеграла. Однако для некоторых функций это может и не быть справедливо.
Впервые анализ этой особенности опубликовал Карл Рунге, немецкий математик, занимавшийся исследованием численных методов.
Он заметил, интерполирующий полином с равномерным разбиением отрезка для функции перестает сходиться в диапазоне значений 0.726.. ≤ |x| 10 применять не рекомендуется.

Для увеличения точности численного интегрирования, можно разбить отрезок на несколько частей — частичных интервалов, и для каждой части отдельно вычислить приближенное значение интеграла. Сумма значений интеграла по всем частичным интервалам даст нам значение интеграла на всем отрезке. Кроме того можно комбинировать различные правила друг с другом в любой последовательности.

Для исследования работы с заданной функцией новых, основанных на формулах Ньютона-Котеса правил, можно воспользоваться базовым калькулятором, в котором веса задаются в явном виде:

Видео:Метод левых, правых и средних прямоугольниковСкачать

Метод прямоугольников

Не всегда имеется возможность вычисления интегралов по формуле Ньютона-Лейбница. Не все подынтегральные функции имеют первообразные элементарных функций, поэтому нахождение точного числа становится нереальным. При решении таких задач не всегда необходимо получать на выходе точные ответы. Существует понятие приближенного значения интеграла, которое задается методом числового интегрирования типа метода прямоугольников, трапеций, Симпсона и другие.

Данная статья посвящена именно этому разделу с получением приближенных значений.

Будет определена суть метода Симпсона, получим формулу прямоугольников и оценки абсолютной погрешности, метод правых и левых треугольников. На заключительном этапе закрепим знания при помощи решения задач с подробным объяснением.

Видео:3.2 Численное интегрирование (лекция)Скачать

Суть метода прямоугольников

Если функция y = f ( x ) имеет непрерывность на отрезке [ a ; b ] и необходимо вычислить значение интеграла ∫ a b f ( x ) d x .

Необходимо воспользоваться понятием неопределенного интеграла. Тогда следует разбить отрезок [ a ; b ] на количество n частей x i — 1 ; x i , i = 1 , 2 , . . . . , n , где a = x 0 x 1 x 2 . . . x n — 1 x n = b . В промежутке отрезка x i — 1 ; x i , i = 1 , 2 , . . . , n выберем точку со значением ζ i . Из определения имеем, что существует определенный тип интегральных сумм при бесконечном уменьшении длины элементарного отрезка, который уже разбили. Это выражается формулой λ = m a x i = 1 , 2 , . . . , n ( x i — x i — 1 ) → 0 , тогда получаем, что любая из таких интегральных сумм – приближенное значение интеграла ∫ a b f ( x ) d x ≈ ∑ i = 1 n f ( ζ i ) · ( x i — x i — 1 ) .

Суть метода прямоугольников выражается в том, что приближенное значение считается интегральной суммой.

Видео:3. Численные методы расчета определенного интеграла: прямоугольников, трапеции, парабол (Симпсона)Скачать

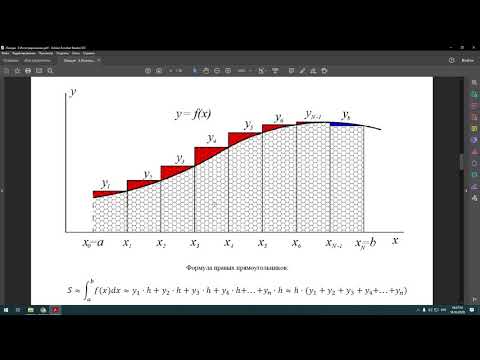
Метод средних прямоугольников

Если разбить интегрируемый отрезок [ a ; b ] на одинаковые части точкой h , то получим a = x 0 , x 1 = x 0 + h , x 2 = x 0 + 2 h , . . . , x — 1 = x 0 + ( n — 1 ) h , x n = x 0 + n h = b , то есть h = x i — x i — 1 = b — a n , i = 1 , 2 , . . . , n . Серединами точек ζ i выбираются элементарные отрезки x i — 1 ; x i , i = 1 , 2 , . . . , n , значит ζ i = x i — 1 + h 2 , i = 1 , 2 , . . . , n .

Тогда приближенное значение ∫ a b f ( x ) d x ≈ ∑ i = 1 n f ( ζ i ) · ( x i — x i — 1 ) записывается таким образом ∫ a b f ( x ) d x ≈ h · ∑ i = 1 n f ( ζ i ) x i — 1 + h 2 . Данная формула называется формулой метода прямоугольников.

Такое название метод получает из-за характера выбора точек ζ i , где шаг разбиения отрезка берется за h = b — a n .

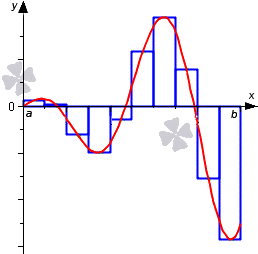
Рассмотрим на приведенном ниже рисунке данный метод.

Чертеж явно показывает, что приближение к кусочной ступенчатой функции

y = f x 0 + h 2 , x ∈ [ x 0 ; x 1 ) f x 1 + h 2 , x ∈ [ x 1 ; x 2 ) . . . f x n — 1 + h 2 , x ∈ [ x n — 1 ; x n ] происходит на всем пределе интегрирования.

С геометрической стороны мы имеем, что неотрицательная функция y = f ( x ) на имеющемся отрезке [ a ; b ] имеет точное значение определенного интеграла и выглядит как криволинейная трапеция, площадь которой необходимо найти. Рассмотрим на рисунке, приведенном ниже.

Видео:Метод левых прямоугольников, разбор задачиСкачать

Оценка абсолютной погрешности метода средних прямоугольников

Для оценки абсолютной погрешности необходимо выполнить ее оценку на заданном интервале. То есть следует найти сумму абсолютных погрешностей каждого интервала. Каждый отрезок x i — 1 ; x i , i = 1 , 2 , . . . , n имеет приближенное равенство ∫ x i — 1 x i f ( x ) d x ≈ f x i — 1 + h 2 · h = f x i — 1 + h 2 · ( x i — x i — 1 ) . Абсолютная погрешность данного метода треугольников δ i , принадлежащей отрезку i , вычисляется как разность точного и приближенного определения интеграла . Имеем, что δ i = ∫ x i — 1 x i f ( x ) d x — f x i — 1 + h 2 · x i — x i — 1 . Получаем, что f x i — 1 + h 2 является некоторым числом, а x i — x i — 1 = ∫ x i — 1 x i d x , тогда выражение f x i — 1 + h 2 · x i — x i — 1 по 4 свойству определения интегралов записывается в форме f x i — 1 + h 2 · x i — x i — 1 = ∫ x — 1 x f x i — 1 + h 2 d x . Отсюда получаем, что отрезок i имеет абсолютную погрешность вида

δ i = ∫ x i — 1 x i f ( x ) d x — f x i — 1 + h 2 · x i — x i — 1 = = ∫ x i — 1 x i f ( x ) d x — ∫ x i — 1 x i x i — 1 + h 2 d x = ∫ x i — 1 x i f ( x ) = — f x i — 1 + h 2 d x

Если взять, что функция y = f ( x ) имеет производные второго порядка в точке x i — 1 + h 2 и ее окрестностях, тогда y = f ( x ) раскладывается в ряд Тейлора по степеням x — x i — 1 + h 2 с остаточным членом в форме разложения по Лагранжу. Получаем, что

f ( x ) = f x i — 1 + h 2 + f ‘ x i — 1 + h 2 · x — x i — 1 + h 2 + + f » ( ε i ) x — x i — 1 + h 2 2 2 ⇔ ⇔ f ( x ) = f ( x i — 1 + h 2 ) = f ‘ x i — 1 + h 2 · x — x i — 1 + h 2 + + f » ( ε i ) x — x i — 1 + h 2 2 2

Исходя из свойства определенного интеграла, равенство может интегрироваться почленно. Тогда получим, что

∫ x i — 1 x i f ( x ) — f x i — 1 + h 2 d x = ∫ x i — 1 x i f ‘ x i — 1 + h 2 · x — x i — 1 + h 2 d x + + ∫ x i — 1 x i f » ε i · x — x i — 1 + h 2 2 2 d x = = f ‘ x i — 1 + h 2 · x — x i — 1 + h 2 2 2 x i — 1 x i + f » ε i · x — x i — 1 + h 2 3 6 x i — 1 x i = = f ‘ x i — 1 + h 2 · x i — h 2 2 2 — x i — 1 — x i — 1 + h 2 2 2 + + f » ε i · x i — h 2 3 6 — x i — 1 — x i — 1 + h 2 3 6 = = f ‘ x i — 1 + h 2 · h 2 8 — h 2 8 + f » ( ε i ) · h 3 48 + h 3 48 = f » ε i · h 3 24

где имеем ε i ∈ x i — 1 ; x i .

Отсюда получаем, что δ i = ∫ x i — 1 x i f ( x ) — f x i — 1 + h 2 d x = f » ε i · h 3 24 .

Абсолютная погрешность формулы прямоугольников отрезка [ a ; b ] равняется сумме погрешностей каждого элементарного интервала. Имеем, что

δ n = ∑ i = 1 n ∫ x i — 1 x i f ( x ) — f x i — 1 + h 2 d x и δ n ≤ m a x x ∈ [ a ; b ] f » ( x ) · n · h 3 24 = m a x x ∈ [ a ; b ] f » ( x ) = b — a 3 24 n 2 .

Неравенство является оценкой абсолютной погрешности метода прямоугольников.

Видео:метод прямоугольниковСкачать

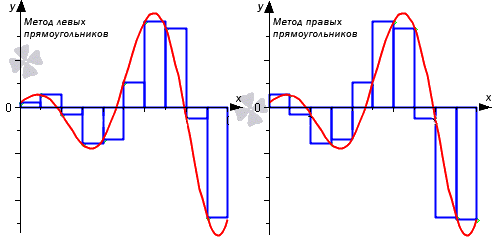
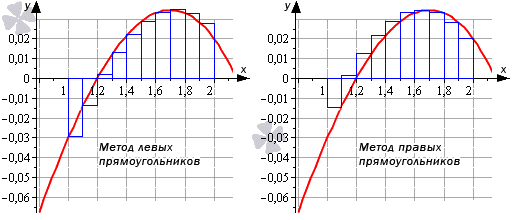
Метод левых прямоугольников и метод правых прямоугольников

Для модификации метода рассмотрим формулы.

∫ a b f ( x ) d x ≈ h · ∑ i = 0 n — 1 f ( x i ) является формулой левых треугольников.

∫ a b f ( x ) d x ≈ h · ∑ i = 1 n f ( x i ) является формулой правых треугольников.

Рассмотрим на примере рисунка, приведенного ниже.

Отличием метода средних прямоугольников считается выбор точек не по центру, а на левой и правой границах данных элементарных отрезков.

Такая абсолютная погрешность методов левых и правых треугольников можно записать в виде

δ n ≤ m a x x ∈ [ a ; b ] f ‘ ( x ) · h 2 · n 2 = m a x x ∈ [ a ; b ] f ‘ ( x ) · ( b — a ) 2 2 n

Видео:Метод средних прямоугольниковСкачать

Примеры применения метода прямоугольников при приближенном вычислении определенных интегралов

Необходимо рассмотреть решение примеров, где нужно вычислять примерное значение имеющегося определенного интеграла при помощи метода прямоугольников. Рассматривают два типа решения заданий. Суть первого случая – задание количества интервалов для разбивания отрезка интегрирования. Суть второго заключается в наличии допустимой абсолютной погрешности.

Формулировки задач выглядят следующим образом:

произвести приближенное вычисление определенного интеграла при помощи метода прямоугольников, разбивая на nколичество отрезков интегрирования;
найти приближенное значение определенного интеграла методом прямоугольников с точностью до одной сотой.

Рассмотрим решения в обоих случаях.

В качестве примера выбрали задания, которые поддаются преобразованию для нахождения их первообразных. Тогда появляется возможность вычисления точного значения определенного интеграла и сравнения с приближенным значением при помощи метода прямоугольников.

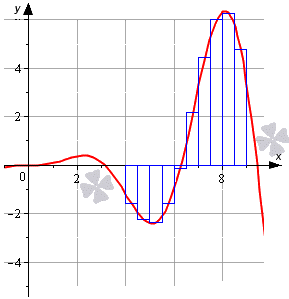
Произвести вычисление определенного интеграла ∫ 4 9 x 2 sin x 10 d x при помощи метода прямоугольников, разбивая отрезок интегрирования на 10 частей.

Из условия имеем, что a = 4 , b = 9 , n = 10 , f ( x ) = x 2 sin x 10 . Для применения ∫ a b f ( x ) d x ≈ h · ∑ i = 1 n f x i — 1 + h 2 необходимо вычислить размерность шага h и значение функции f ( x ) = x 2 sin x 10 в точках x i — 1 + h 2 , i = 1 , 2 , . . . , 10 .

Вычисляем значение шага и получаем, что

h = b — a n = 9 — 4 10 = 0 . 5 .

Потому как x i — 1 = a + ( i — 1 ) · h , i = 1 , . . . , 10 , тогда x i — 1 + h 2 = a + ( i — 1 ) · h + h 2 = a + i — 0 . 5 · h , i = 1 , . . . , 10 .

Так как i = 1 , то получаем x i — 1 + h 2 = x 0 + h 2 = a + ( i — 0 . 5 ) · h = 4 + ( 1 — 0 . 5 ) · 0 . 5 = 4 . 25 .

После чего необходимо найти значение функции

f x i — 1 + h 2 = f x 0 + h 2 = f ( 4 . 25 ) = 4 . 25 2 sin ( 4 . 25 ) 10 ≈ — 1 . 616574

При i = 2 получаем x i — 1 + h 2 = x 1 + h 2 = a + i — 0 . 5 · h = 4 + ( 2 — 0 . 5 ) · 0 . 5 = 4 . 75 .

Нахождение соответствующего значения функции получает вид

f x i — 1 + h 2 = f x 1 + h 2 = f ( 4 . 75 ) = 4 . 75 2 sin ( 4 . 75 ) 10 ≈ — 2 . 254654

Вычисления производятся до i = 10 .

Представим эти данные в таблице, приведенной ниже.

i	1	2	3	4	5
x i — 1 + h 2	4 . 25	4 . 75	5 . 25	5 . 75	6 . 25
f x i — 1 + h 2	— 1 . 616574	— 2 . 254654	— 2 . 367438	— 1 . 680497	— 0 . 129606

i	6	7	8	9	10
x i — 1 + h 2	6 . 75	7 . 25	7 . 75	8 . 25	8 . 75
f x i — 1 + h 2	2 . 050513	4 . 326318	5 . 973808	6 . 279474	4 . 783042

Значения функции необходимо подставить в формулу прямоугольников. Тогда получаем, что

∫ 4 9 x 2 sin x 10 d x ≈ h · ∑ i = 1 n f x i — 1 + h 2 = = 0 . 5 · — 1 . 616574 — 2 . 25654 — 2 . 367438 — 1 . 680497 — 0 . 129606 + + 2 . 050513 + 4 . 326318 + 5 . 973808 + 6 . 279474 + 4 . 783042 = = 7 . 682193

Исходный интеграл можно вычислить при помощи формулы Ньютона-Лейбница. Получаем, что

∫ 4 9 x 2 · sin x 10 d x = — 1 10 x 2 · cos x + 1 5 x · sin x + 1 5 cos x 4 9 = = 7 5 cos 4 — 4 5 sin 4 — 79 10 cos 9 + 9 5 sin 9 ≈ 7 . 630083

Находим первообразную выражения — 1 10 x 2 · cos x + 1 5 x · sin x + 1 5 cos x соответствующую функции f ( x ) = x 2 sin x 10 . Нахождение производится методом интегрирования по частям.

Отсюда видно, что определенный интеграл отличается от значения, полученном при решении методом прямоугольников, где n = 10 , на 6 долей единицы. Рассмотрим на рисунке, приведенном ниже.

Вычислить приближенного значение определенного интеграла ∫ 1 2 ( — 0 . 03 x 3 + 0 . 26 x — 0 . 26 ) d x при помощи метода левых и правых прямоугольников с точностью до одной сотой.

Из условия мы имеем, что a = 1 , b = 2 и f ( x ) = — 0 . 03 x 3 + 0 . 26 x — 0 . 26 .

Для применения формулы правых и левых прямоугольников нужно знать размерность шага h , а для его вычисления разбиваем отрезок интегрирования на n отрезков. По условию имеем, что точность должна быть до 0 , 01 , тогда нахождение n возможно при помощи оценки абсолютной погрешности методов левых и правых прямоугольников.

Известно, что δ n ≤ m a x x ∈ [ a ; b ] f ‘ ( x ) · ( b — a ) 2 2 n . Для достижения необходимой степени точности необходимо найти такое значение n , для которого неравенство m a x x ∈ [ a ; b ] f ‘ ( x ) · ( b — a ) 2 2 n ≤ 0 . 01 будет выполнено.

Найдем наибольшее значение модуля первой производной, то есть значение m a x x ∈ [ a ; b ] f ‘ ( x ) подынтегральной функции f ( x ) = — 0 . 03 x 3 + 0 . 26 x — 0 . 26 , определенной на отрезке [ 1 ; 2 ] . В нашем случае необходимо выполнить вычисления:

f ‘ ( x ) = — 0 . 03 x 3 + 0 . 26 x — 0 . 26 ‘ = — 0 . 09 x 2 + 0 . 26

Парабола является графиком подынтегральной функции с ветвями, направленными вниз, определенная на отрезке [ 1 ; 2 ] , причем с монотонно убывающим графиком. Необходимо произвести вычисление модулей значений производных на концах отрезков, а из них выбрать наибольшее значение. Получаем, что

f ‘ ( 1 ) = — 0 . 09 · 1 2 + 0 . 26 = 0 . 17 f ‘ ( 2 ) = — 0 . 09 · 2 2 + 0 . 26 = 0 . 1 → m a x x ∈ [ 1 ; 2 ] f ‘ ( x ) = 0 . 17

Решение сложных подынтегральных функций подразумевает обращение к разделу наибольше и наименьшее значение функции.

Тогда получаем, что наибольшее значение функции имеет вид:

m a x x ∈ [ a ; b ] f ‘ ( x ) · ( b — a ) 2 2 n ≤ 0 . 01 ⇔ ⇔ 0 . 17 · ( 2 — 1 ) 2 2 n ≤ 0 . 01 ⇔ 0 . 085 n ≤ 0 . 01 ⇔ n ≥ 8 . 5

Дробность числа n исключается, так как n является натуральным числом. Чтобы прийти к точности 0 . 01 , используя метод правых и левых прямоугольников, не обходимо выбирать любое значение n . Для четкости расчетов возьмем n = 10 .

Тогда формула левых прямоугольников примет вид ∫ a b f ( x ) d x ≈ h · ∑ i = 0 n — 1 f ( x i ) , а правых — ∫ a b f ( x ) d x ≈ h · ∑ i = 1 n f ( x i ) . Для применения их на практике необходимо найти значение размерности шага h и f ( x i ) , i = 0 , 1 , . . . , n , где n = 10 .

h = b — a n = 2 — 1 10 = 0 . 1

Определение точек отрезка [ a ; b ] производится с помощью x i = a + i · h , i = 0 , 1 , . . . , n .

При i = 0 , получаем x i = x 0 = a + i · h = 1 + 0 · 0 . 1 = 1 и f ( x i ) = f ( x 0 ) = f ( 1 ) = — 0 . 03 · 1 3 + 0 . 26 · 1 — 0 . 26 = — 0 . 03 .

При i = 1 , получаем x i = x 1 = a + i · h = 1 + 1 · 0 . 1 = 1 . 1 и f ( x i ) = f ( x 1 ) = f ( 1 . 1 ) = — 0 . 03 · ( 1 . 1 ) 3 + 0 . 26 · ( 1 . 1 ) — 0 . 26 = — 0 . 01393 .

Вычисления производятся до i = 10 .

Вычисления необходимо представить в таблице, приведенной ниже.

i	0	1	2	3	4	5
x i	1	1 . 1	1 . 2	1 . 3	1 . 4	1 . 5
f ( x i )	— 0 . 03	— 0 . 01393	0 . 00016	0 . 01209	0 . 02168	0 . 02875

i	6	7	8	9	10
x i	1 . 6	1 . 7	1 . 8	1 . 9	2
f ( x i )	0 . 03312	0 . 03461	0 . 03304	0 . 02823	0 . 02

Подставим формулу левых треугольников

∫ 1 2 ( — 0 . 03 x 3 + 0 . 26 x — 0 . 26 ) d x ≈ h · ∑ i = 0 n — 1 f ( x i ) = = 0 . 1 · — 0 . 03 — 0 . 01393 + 0 . 00016 + 0 . 01209 + 0 . 02168 + + 0 . 02875 + 0 . 03312 + 0 . 03461 + 0 . 03304 + 0 . 02823 = = 0 . 014775

Подставляем в формулу правых треугольников

∫ 1 2 ( — 0 . 03 x 3 + 0 . 26 x — 0 . 26 ) d x ≈ h · ∑ i = 1 n f ( x i ) = = 0 . 1 · — 0 . 01393 + 0 . 00016 + 0 . 01209 + 0 . 02168 + 0 . 02875 + + 0 . 03312 + 0 . 03461 + 0 . 03304 + 0 . 02823 + 0 . 02 = 0 . 019775

Произведем вычисление по формуле Ньютона-Лейбница:

∫ 1 2 ( — 0 . 03 x 3 + 0 . 26 x — 0 . 26 ) d x = = — 0 . 03 x 4 4 + 0 . 13 x 2 — 0 . 26 x 1 2 = 0 . 0175

Рассмотрим рисунок, приведенный ниже.

Видео:Метод СимпсонаСкачать

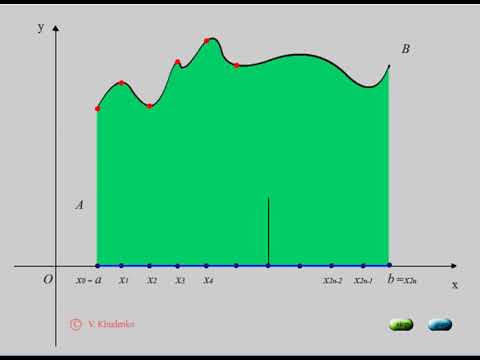
Замечание

Нахождение наибольшего значения модуля первой производной является трудоемкой работой, поэтому можно исключить использование неравенства для оценивания абсолютной погрешности и методов численного интегрирования. Разрешено применять схему.

Берем значение n = 5 для вычисления приближенного значения интеграла. Необходимо удвоить количество отрезков интегрирования, тогда n = 10 , после чего производится вычисление примерного значения. необходимо найти разность этих значений при n = 5 и n = 10 . Когда разность не соответствует требуемой точности, то приближенным значением считается n = 10 с округлением до десятка.

Когда погрешность превышает необходимую точность, то производится удваивание n и сравнивание приближенных значений. Вычисления производятся до тех пор, пока необходимая точность не будет достигнута.

Для средних прямоугольников выполняются аналогичные действия, но вычисления на каждом шаге требуют разности полученных приближенных значений интеграла для n и 2 n . Такой способ вычисления называется правилом Рунге.

Произведем вычисление интегралов с точностью до одной тысячной при помощи метода левых прямоугольников.

При n = 5 получаем, что ∫ 1 2 ( — 0 . 03 x 3 + 0 . 26 x — 0 . 26 ) d x ≈ 0 . 0116 , а при n = 10 — ∫ 1 2 ( — 0 . 03 x 3 + 0 . 26 x — 0 . 26 ) d x ≈ 0 . 014775 . Так как имеем, что 0 . 0116 — 0 . 014775 = 0 . 003175 > 0 . 001 , возьмем n = 20 . Получаем, что ∫ 1 2 ( — 0 . 03 x 3 + 0 . 26 x — 0 . 26 ) d x ≈ 0 . 01619375 . Имеем 0 . 014775 — 0 . 01619375 = 0 . 00141875 > 0 . 001 , возьмем значение n = 40 , тогда получим ∫ 1 2 ( — 0 . 03 x 3 + 0 . 26 x — 0 . 26 ) d x ≈ 0 . 01686093 . Имеем, что 0 . 1619375 — 0 . 01686093 = 0 . 00066718 0 . 001 , тогда после округления значения проверим, что ∫ 1 2 ( — 0 . 03 x 3 + 0 . 26 x — 0 . 26 ) d x равняется значению 0 , 017 с погрешностью 0 , 001 . Из оценок абсолютных погрешностей видно, что данный метод дает максимальную точность в отличие от метода левых и правых координат для заданного n . Отдается предпочтение методу средних прямоугольников.

Непрерывные подынтегральные функции при бесконечном разделении на отрезки данное приближенно число стремится к точному. Чаще всего такой метод выполняется при помощи специальных программ на компьютере. Поэтому чем больше значение n , тем больше вычислительная погрешность.

Для наиболее точного вычисления необходимо выполнять точные промежуточные действия, желательно с точностью до 0 , 0001 .

Видео:12й класс; Информатика; "Вычисление определённого интеграла методом прямоугольников"Скачать

Итоги

Для вычисления неопределенного интеграла методом прямоугольников следует применять формулу такого вида ∫ a b f ( x ) d x ≈ h · ∑ i = 1 n f ( ζ i ) x i — 1 + h 2 и оценивается абсолютная погрешность с помощью δ n ≤ m a x x ∈ [ a ; b ] f ‘ ‘ ( x ) · n · h 3 24 = m a x x ∈ [ a ; b ] f ‘ ‘ ( x ) · b — a 3 24 n 2 .

Для решения с помощью методов правых и левых прямоугольников применяют формулы, имеющие вид, ∫ a b f ( x ) d x ≈ h · ∑ i = 0 n — 1 f ( x i ) и ∫ a b f ( x ) d x ≈ h · ∑ i = 1 n f ( x i ) . Абсолютная погрешность оценивается при помощи формулы вида δ n ≤ m a x x ∈ [ a ; b ] f ‘ ( x ) · h 2 · n 2 = m a x x ∈ [ a ; b ] f ‘ ( x ) · b — a 2 2 n .

Видео:Метод трапеций при вычислении определенного интегралаСкачать

Метод левых треугольников интеграл

Задача численного интегрирования состоит в замене исходной подинтегральной функции f(x), для которой трудно или невозможно записать первообразную в аналитике, некоторой аппроксимирующей функцией φ(x). Такой функцией обычно является полином (кусочный полином) . То есть:
,
где – априорная погрешность метода на интервале интегрирования,
а r(x) – априорная погрешность метода на отдельном шаге интегрирования.

Обзор методов интегрирования.

Методы вычисления однократных интегралов называются квадратурными (для кратных интегралов – кубатурными).

Методы Ньютона-Котеса.

φ(x)

Методы статистических испытаний (методы Монте-Карло). Здесь узлы сетки для квадратурного или кубатурного интегрирования выбираются с помощью датчика случайных чисел, ответ носит вероятностный характер. В основном применяются для вычисления кратных интегралов.

Сплайновые методы. Здесь φ(x) – кусочный полином с условиями связи между отдельными полиномами посредством системы коэффициентов.

Методы наивысшей алгебраической точности. Обеспечивают оптимальную расстановку узлов сетки интегрирования и выбор весовых коэффициентов ρ(x) в задаче

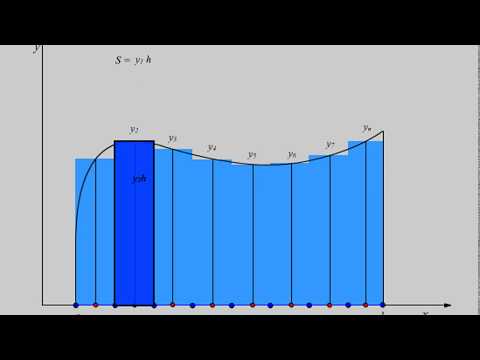
. Сюда относится метод Гаусса-Кристоффеля (вычисление несобственных интегралов) и метод Маркова.

Различают метод левых, правых и средних прямоугольников. Суть метода ясна из рисунка. На каждом шаге интегрирования функция аппроксимируется полиномом нулевой степени – отрезком, параллельным оси абсцисс.

Выведем формулу метода прямоугольников из анализа разложения функции f(x) в ряд Тейлора вблизи некоторой точки x = x_i.

…

Рассмотрим диапазон интегрирования от x_i до x_i+h, где h – шаг интегрирования.

Вычислим …=

= = . Получили формулу правых (или левых) прямоугольников и априорную оценку погрешности r на отдельном шаге интегрирования. Основной критерий, по которому судят о точности алгоритма – степень при величине шага в формуле априорной оценки погрешности.

В случае равного шага h на всем диапазоне интегрирования общая формула имеет вид

Здесь n – число разбиений интервала интегрирования, . Для справедливости существования этой оценки необходимо существование непрерывной f'(x).

Метод средних прямоугольников. Здесь на каждом интервале значение функции считается в точке , то есть . Разложение функции в ряд Тейлора показывает, что в случае средних прямоугольников точность метода существенно выше:

Аппроксимация в этом методе осуществляется полиномом первой степени. Суть метода ясна из рисунка.

На единичном интервале
.
В случае равномерной сетки (h = const )

При этом , а . Погрешность метода трапеций в два раза выше, чем у метода средних прямоугольников! Однако на практике найти среднее значение на элементарном интервале можно только у функций, заданных аналитически (а не таблично), поэтому использовать метод средних прямоугольников удается далеко не всегда. В силу разных знаков погрешности в формулах трапеций и средних прямоугольников истинное значение интеграла обычно лежит между двумя этими оценками.

Особенности поведения погрешности.

Казалось бы, зачем анализировать разные методы интегрирования, если мы можем достичь высокой точности, просто уменьшая величину шага интегрирования. Однако рассмотрим график поведения апостериорной погрешности R результатов численного расчета в зависимости от числа n разбиений интервала (то есть при шаг . На участке (1) погрешность уменьшается в связи с уменьшением шага h. Но на участке (2) начинает доминировать вычислительная погрешность, накапливающаяся в результате многочисленных арифметических действий. Таким образом, для каждого метода существует своя R_min, которая зависит от многих факторов, но прежде всего от априорного значения погрешности метода R.

Уточняющая формула Ромберга.

Метод Ромберга заключается в последовательном уточнении значения интеграла при кратном увеличении числа разбиений. В качестве базовой может быть взята формула трапеций с равномерным шагом h.
Обозначим интеграл с числом разбиений n = 1 как .
Уменьшив шаг в два раза, получим .
Если последовательно уменьшать шаг в 2 n раз, получим рекуррентное соотношение для расчета .

Пусть мы вычислили четыре раза интеграл с n от 1 до 4. Представим следующий треугольник:
R(1;1)
R(2;1) R(2;2)
R(3;1) R(3;2) R(3;3)
R(4;1) R(4;2) R(4;3) R(4;4)

В первом столбце стоят значения интеграла, полученные при последовательном удвоении числа интервалов. Следующие столбцы – результаты уточнения значения интеграла по следующей рекуррентной формуле:

Правое нижнее значение в треугольнике – искомое уточненное значение интеграла.

Подынтегральная функция f(x) заменяется интерполяционным полиномом второй степени P(x) – параболой, проходящей через три узла, например, как показано на рисунке ((1) – функция, (2) – полином).

Рассмотрим два шага интегрирования (h = const = x_i+1 – x_i), то есть три узла x₀, x₁, x₂, через которые проведем параболу, воспользовавшись уравнением Ньютона:
.
Пусть z = x — x₀,
тогда

Теперь, воспользовавшись полученным соотношением, сосчитаем интеграл по данному интервалу:

.

В итоге .
Для равномерной сетки и четного числа шагов n формула Симпсона принимает вид:

Здесь , а в предположении непрерывности четвертой производной подынтегральной функции.

Методы Монте-Карло.

1) одномерная случайная величина – статистический вариант метода прямоугольников.
В качестве текущего узла x_i берется случайное число, равномерно распределенное на интервале интегрирования [a, b]. Проведя N вычислений, значение интеграла определим по следующей формуле: . Для R можно утверждать хотя бы

2) двумерная случайная величина– оценка площадей.

Рассматриваются две равномерно распределенных случайных величины x_i и y_i, которые можно рассматривать как координаты точки в двумерном пространстве. За приближенное значение интеграла принимается количества точек S, попавших под кривую y = f(x), к общему числу испытаний N, т.е. .