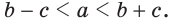Меньшей стороной треугольника abc является (6 видео)

Меньшей стороной треугольника abc является

§ 16. Сумма углов треугольника

Треугольник — ключевая фигура планиметрии. Мир треугольников разнообразен. Но всем им присуще свойство, которое раскрывает следующая теорема.

Сумма углов треугольника равна 180° .

Рассмотрим произвольный треугольник ABC . Требуется доказать, что ∠ A + ∠ B + ∠ C = 180°.

Через вершину B проведём прямую a , параллельную прямой AC (рис. 243). Имеем: ∠ A и ∠ 1 равны как накрест лежащие при параллельных прямых a и AC и секущей AB . Аналогично доказываем, что ∠ C = ∠ 3. Но углы 1, 2, 3 составляют развёрнутый угол с вершиной B . Следовательно, ∠ A + ∠ ABC + ∠ C = ∠ 1 + ∠ 2 + ∠ 3 = 180°.

Среди углов треугольника хотя бы два угла острые.

Докажите это следствие самостоятельно.

Из этого следствия вытекает, что угол при основании равнобедренного треугольника всегда острый.

Внешним углом треугольника называют угол, смежный с углом этого треугольника.

На рисунке 244 углы 1, 2, 3 являются внешними углами треугольника ABC .

Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.

На рисунке 244 углы 1, 2 и 3 — внешние углы треугольника АВС . Надо доказать, что ∠ 1 = ∠ 5 + ∠ 6, ∠ 2 = ∠ 4 + ∠ 6, ∠ 3 = ∠ 4 + ∠ 5.

Докажем, например, первое из этих трёх равенств (остальные равенства доказывают аналогично).

По свойству смежных углов ∠ 1 + ∠ 4 = 180°. По теореме о сумме углов треугольника ∠ 4 + ∠ 5 + ∠ 6 = 180°. Тогда ∠ 1 + ∠ 4 = ∠ 4 + ∠ 5 + ∠ 6, отсюда ∠ 1 = ∠ 5 + ∠ 6.

Внешний угол треугольника больше каждого из углов треугольника, не смежных с ним.

Докажите это следствие самостоятельно.

Каждая сторона треугольника меньше суммы двух других его сторон.

Рассмотрим треугольник ABC (рис. 245). Надо доказать, что: 1) AB AC + CB ; 2) AC AB + BC ; 3) BC BA + AC .

Докажем первое из этих неравенств (два других доказывают аналогично).

Пусть доказываемое неравенство неверно. Тогда AB > AC + CB или AB = AC + CB .

1) Пусть AB > AC + CB . Тогда на стороне AB можно отметить точки C 1 и C 2 такие, что AC = AC 1 и BC = BC 2 . Поскольку мы предположили, что AB > AC + CB , то AB > AC 1 + BC 2 . Следовательно, отрезки AC 1 и BC 2 не имеют общих точек (см. рис. 245).

Углы AC 1 C и BC 2 C являются острыми как углы при основании равнобедренных треугольников AC 1 C и BC 2 C соответственно. Тогда углы 1 и 2 являются тупыми как углы, смежные с острыми. Получили противоречие: в треугольнике С 1 СС 2 два тупых угла.

2) Рассуждая аналогично, можно показать (сделайте это самостоятельно), что равенство AB = AC + CB тоже приводит к противоречию.

Из доказанной теоремы следует, что если длина одного из трёх данных отрезков не меньше суммы длин двух других, то эти отрезки не могут служить сторонами треугольника (рис. 246).

В § 23 вы узнаете, что если любой из трёх данных отрезков меньше суммы двух других, то эти отрезки могут служить сторонами треугольника.

Вы уже знаете, что в треугольнике против равных сторон лежат равные углы, и наоборот, против равных углов лежат равные стороны (§ 9, 10). Эти свойства дополняет следующая теорема.

В треугольнике против большей стороны лежит больший угол и, наоборот, против большего угла лежит бóльшая сторона.

1) Рассмотрим треугольник ABC , у которого AB > BC . Надо доказать, что ∠ ACB > ∠ A (рис. 247).

Поскольку AB > BC , то на стороне AB найдётся такая точка M , что BM = BC . Получили равнобедренный треугольник MBC , в котором ∠ BMC = ∠ BCM .

Так как угол BMC — внешний угол треугольника AMC , то ∠ BMC > ∠ A . Следующая «цепочка» доказывает первую часть теоремы:

∠ ACB > ∠ MCB = ∠ BMC > ∠ A .

2) Рассмотрим треугольник ABC , у которого ∠ C > ∠ A . Надо доказать, что AB > BC .

Поскольку ∠ ACB > ∠ A , то угол ACB можно разделить на два угла ACM и MCB так, что ∠ ACM = ∠ A (рис. 248). Тогда треугольник AMC — равнобедренный с равными сторонами MA и MC .

Для стороны BC запишем неравенство треугольника: MB + MC > BC . Учитывая, что MA = MC и MB + MA = AB , получим: AB > BC .

Заметим, что вторую часть теоремы 16.4 можно доказать методом от противного: предположить, что BC ≥ AB , а далее воспользоваться уже доказанной первой частью теоремы. Проведите это доказательство самостоятельно.

Задача. Медиана CM треугольника ABC равна половине стороны AB . Докажите, что треугольник ABC — прямоугольный.

Решение. По условию AM = CM (рис. 249). Тогда в треугольнике AMC углы A и ACM равны.

По условию BM = CM , и в треугольнике BMC углы B и BCM равны.

В треугольнике ACB имеем: ∠ A + ∠ B + + ∠ ACB = 180°. Учитывая, что ∠ A = ∠ ACM и ∠ B = ∠ BCM , получаем: ∠ ACM + ∠ BCM + + ∠ ACB = 180°. Так как ∠ ACM + ∠ BCM = ∠ ACB , то 2 ∠ ACB = 180°. Тогда ∠ ACB = 90°.

Следовательно, треугольник ABC — прямоугольный.

Чему равна сумма углов треугольника?
Какое наименьшее количество острых углов есть в любом треугольнике?
Какой угол называют внешним углом треугольника?
Как связаны внешний угол треугольника и два угла треугольника, не смежные с ним?
Сравните внешний угол треугольника с углом треугольника, не смежным с ним.
Сформулируйте теорему о неравенстве треугольника.
Сформулируйте теорему о соотношении между сторонами и углами треугольника.

357. Найдите угол треугольника, если два других его угла равны 35° и 96°.

358. Один из углов треугольника в 3 раза меньше другого угла и на 35° меньше третьего. Найдите углы треугольника.

359. Найдите углы треугольника, если их градусные меры относятся как 2 : 3 : 7.

360. Найдите углы равностороннего треугольника.

361. Найдите углы равнобедренного прямоугольного треугольника.

362. Угол при основании равнобедренного треугольника равен 63°. Найдите угол при вершине этого треугольника.

363. Найдите углы при основании равнобедренного треугольника, если угол при вершине равен 104°.

364. Найдите углы равнобедренного треугольника, если угол при вершине в 4 раза больше угла при основании.

365. Найдите углы равнобедренного треугольника, если угол при основании на 48° меньше угла при вершине.

366. Найдите углы равнобедренного треугольника, если один из них равен: 1) 110°; 2) 50°. Сколько решений имеет задача?

367. Найдите углы равнобедренного треугольника, если один из них равен: 1) 42°; 2) 94°. Сколько решений имеет задача?

368. Могут ли стороны треугольника быть равными:

1) 6 см, 5 см, 12 см; 2) 6 см, 5 см, 11 см?

369. В треугольнике ABC известно, что ∠ C = 90°, AK — биссектриса, ∠ BAK = 18°. Найдите углы AKC и ABC .

370. В треугольнике ABC известно, что AB = BC , CK — биссектриса, ∠ A = 66°. Найдите ∠ AKC .

371. Биссектрисы AK и CM треугольника ABC пересекаются в точке O , ∠ BAC = 116°, ∠ BCA = 34°. Найдите ∠ AOC .

372. В равнобедренном треугольнике ABC с углом при вершине B , равным 36°, провели биссектрису AD . Докажите, что треугольники ADB и CAD — равнобедренные.

373. В треугольнике ABC провели биссектрису BF . Найдите угол C , если ∠ A = 39°, ∠ AFB = 78°.

374. Докажите, что если один из углов треугольника равен сумме двух других углов, то этот треугольник — прямоугольный.

375. На рисунке 250 укажите внешние углы:

1) при вершинах E и F треугольника MEF ;

2) при вершине E треугольника MKE .

376. На рисунке 251 укажите треугольники, для которых внешним углом является: 1) угол AMB ; 2) угол BMD .

377. Один из внешних углов треугольника равен 75°. Чему равны:

1) угол треугольника при этой вершине;

2) сумма двух углов треугольника, не смежных с ним?

378. Может ли внешний угол треугольника быть меньше смежного с ним угла треугольника? В случае положительного ответа укажите вид треугольника.

379. Определите вид треугольника, если один из его внешних углов равен смежному с ним углу треугольника.

380. Один из внешних углов треугольника равен 136°, а один из углов треугольника, не смежный с ним, — 61°. Найдите второй угол треугольника, не смежный с данным внешним.

381. Один из внешних углов треугольника равен 154°. Найдите углы треугольника, не смежные с ним, если один из этих углов на 28° больше другого.

382. Один из внешних углов треугольника равен 98°. Найдите углы треугольника, не смежные с ним, если один из этих углов в 6 раз меньше другого.

383. Найдите углы равнобедренного треугольника, если внешний угол при его вершине равен 38°.

384. Сравните углы треугольника ABC , если:

1) AB > AC > BC ; 2) AB = BC , BC > AC .

385. В треугольнике ABC известно, что ∠ A = 34°, ∠ B = 28°. Сравните стороны AB , BC и AC .

386. Сравните стороны треугольника ABC , если:

1) ∠ C > ∠ A > ∠ B ; 2) ∠ B > ∠ C , ∠ A = ∠ B .

387. Докажите, что если два угла одного треугольника равны соответственно двум углам другого треугольника, то и третьи углы этих треугольников равны.

388. Найдите углы равнобедренного треугольника, если один из его внешних углов равен: 1) 54°; 2) 112°. Сколько решений имеет задача?

389. Внешний угол равнобедренного треугольника равен 130°. Найдите углы треугольника. Сколько решений имеет задача?

390. Периметр треугольника равен 30 см. Может ли одна из его сторон быть равной: 1) 20 см; 2) 15 см?

391. Длины двух сторон треугольника равны 7 и 9 см. Может ли периметр этого треугольника быть равным: 1) 20 см; 2) 32 см; 3) 18 см?

392. Существует ли треугольник, одна из сторон которого на 2 см меньше второй и на 6 см меньше третьей, а периметр равен 20 см?

393. Биссектрисы углов при основании AC равнобедренного треугольника ABC пересекаются в точке O . Докажите, что угол AOC равен внешнему углу треугольника ABC при вершине A .

394. На рисунке 252 BC ‖ AD , ∠ A = 25°, ∠ B = 55°. Найдите угол CMD .

395. Отрезок BK — биссектриса равнобедренного треугольника ABC с основанием BC , ∠ AKB = 105°. Найдите углы треугольника ABC .

396. На стороне AB треугольника ABC отметили точку D так, что BD = BC , ∠ ACD = 15°, ∠ DCB = 40°. Найдите углы треугольника ABC .

397. На сторонах треугольника ABC (рис. 253) отметили точки E и F так, что ∠ 1 = ∠ 2. Докажите, что ∠ 3 = ∠ 4.

398. На рисунке 254 BC ‖ AD , ∠ B = 100°, ∠ ACD = 95°, ∠ D = 45°. Докажите, что AB = BC .

399. Через вершину C треугольника ABC проведена прямая, параллельная биссектрисе AM треугольника и пересекающая прямую AB в точке K . Найдите углы треугольника AKC , если ∠ BAC = 70°.

400. В треугольнике ABC биссектрисы углов A и C пересекаются в точке O . Найдите ∠ AOC , если ∠ B = 100°.

401. Докажите, что биссектриса внешнего угла при вершине равнобедренного треугольника параллельна его основанию.

402. Докажите, что если биссектриса внешнего угла треугольника параллельна его стороне, то этот треугольник равнобедренный.

403. Угол при основании AC равнобедренного треугольника ABC в 2 раза больше угла при вершине, AM — биссектриса треугольника. Докажите, что BM = AC .

404. Треугольник ABC равнобедренный с основанием AC . На стороне BC отметили точку M так, что BM = AM = AC . Найдите углы треугольника ABC .

405. Докажите, что в любом треугольнике существует угол: 1) не меньше 60°; 2) не больше 60°.

406. Определите вид треугольника, если:

1) один из его углов больше суммы двух других;

2) любой из его углов меньше суммы двух других.

407. Определите вид треугольника, если сумма любых двух его углов больше 90°.

408. В треугольнике ABC угол B — тупой. На продолжении стороны AB за точку A отметили произвольную точку D . Докажите, что CD > AC .

409. В треугольнике ABC известно, что ∠ C > 90°. На стороне BC отметили произвольную точку D . Докажите, что AD > AC .

410. Существует ли треугольник, две биссектрисы которого перпендикулярны?

411. Существует ли треугольник, в котором одна биссектриса делит пополам другую биссектрису?

412. Найдите углы треугольника ABC , если биссектриса угла B разбивает его на два равнобедренных треугольника.

413. Три точки A , B и C таковы, что выполняется равенство AB = AC + CB . Докажите, что точка C является внутренней точкой отрезка AB .

414. На прямой m (рис. 255) найдите такую точку C , чтобы сумма расстояний от неё до точек A и B была наименьшей. Ответ обоснуйте.

415. Одна сторона треугольника равна 2,8 см, а вторая — 0,6 см. Найдите третью сторону этого треугольника, если её длина, выраженная в сантиметрах, равна целому числу.

416. В треугольнике ABC известно, что ∠ A = α , биссектрисы внешних углов при вершинах B и C пересекаются в точке O . Найдите ∠ BOC .

417. Отрезок AM — медиана треугольника ABC , ∠ CAM > ∠ BAM . Докажите, что AB > AC .

418. На боковых сторонах AB и BC равнобедренного треугольника ABC отметили соответственно точки E и F так, что AC = AF = EF = BE . Найдите углы треугольника ABC .

419. В треугольнике ABC известно, что AB = 2 см, ∠ A = 60°, ∠ B = 70°. На стороне AC отметили точку D так, что AD = 1 см. Найдите углы треугольника BDC .

420. Докажите, что сумма длин двух сторон треугольника больше удвоенной длины медианы, проведённой к третьей стороне.

Упражнения для повторения

421. На прямой отметили точки A , B и C так, что точка B лежит между точками A и C и BC = 2 AB . На отрезке BC отметили точку D так, что BD : DC = 3 : 7. Найдите расстояние между серединами отрезков AB и CD , если отрезок CD на 16 см длиннее отрезка BD .

422. На медиане BM треугольника ABC отметили точку O так, что ∠ OAC = ∠ OCA . Докажите, что треугольник ABC — равнобедренный.

Наблюдайте, рисуйте, конструируйте, фантазируйте

423. Существует ли шестиугольник, у которого никакие две диагонали не имеют общих точек, отличных от вершин?

Содержание

Неравенство треугольника — определение и вычисление с примерами решения
Неравенство треугольника
Пробный экзаменационный вариант «ОГЭ математика пробник 130 вариант» (2022)
📸 Видео

Видео:№156. Периметр треугольника ABC равен 15 см. Сторона ВС больше стороны АВ на 2 см, а сторона ABСкачать

Неравенство треугольника — определение и вычисление с примерами решения

Содержание:

Неравенство треугольника:

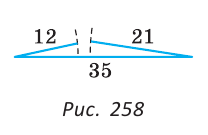
Опыт нам подсказывает, что путь из точки А в точку С по прямой АС короче, чем по ломаной ABC (рис. 255), т. е. АС 12+21 (рис. 258).

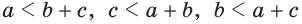
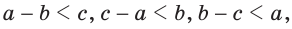
Замечание. Из неравенств треугольника следует, что то есть любая сторона треугольника больше разности двух других его сторон. Так, для стороны а справедливо

Пример:

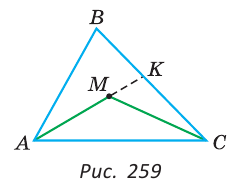
Внутри треугольника ABC взята точка М (рис. 259). Доказать, что периметр треугольника АМС меньше периметра треугольника ABC.

Решение:

Так как у треугольников ABC и АМС сторона АС — общая, то достаточно доказать, что AM + МС B (рис. 108, а).

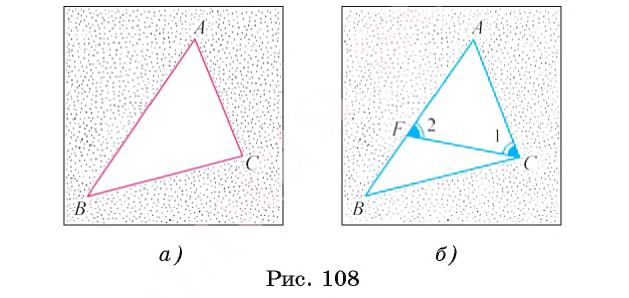
2) Отложим на стороне АВ отрезок АF, равный стороне AC (рис. 108, б).

3) Так как АF 1.

4) Угол 2 является внешним углом треугольника ВFС, следовательно, 2 > B.

5) Так как треугольник FАС является равнобедренным, то 1 = 2.

Таким образом, BСА > 1, 1 = 2 и 2 > B.

Отсюда получаем, что ВСА > B.

Теорема 2. В треугольнике против большего угла лежит большая сторона.

1) Пусть в треугольнике АBС С > B. Докажем, что АВ > АС (см. рис. 108, а). Доказательство проведем методом от противного.

2) Предположим, что это не так. Тогда: либо АВ = АС, либо АВ C.

В каждом из этих случаев получаем противоречие с условием: C > B. Таким образом, сделанное предположение неверно и, значит, АВ > АС.

Из данной теоремы следует утверждение: в прямоугольном треугольнике катет меньше гипотенузы.

Действительно, гипотенуза лежит против прямого угла, а катет — против острого. Поскольку прямой угол больше острого, то по теореме 2 получаем, что гипотенуза больше катета.

Теорема 3 (признак равнобедренного треугольника). Если два угла треугольника равны, то треугольник равнобедренный.

Пусть в треугольнике два угла равны. Тогда равны стороны, лежащие против этих углов. В самом деле, если предположить, что одна из указанных сторон больше другой, то по теореме 1 угол, лежащий против этой стороны, будет больше угла, лежащего против другой стороны, что противоречит условию равенства углов.

Значит, наше предположение неверно и в треугольнике две стороны равны, т. е. треугольник является равнобедренным.

Неравенство треугольника

Докажем, что длина каждой стороны треугольника меньше суммы длин двух других сторон.

Теорема 4. Длина каждой стороны треугольника меньше суммы длин двух других его сторон.

1) Пусть ABC — произвольный треугольник. Докажем, например, что выполняется неравенство АВ l, следовательно, верно неравенство АВF > 2.

4) Так как в треугольнике против большего угла лежит большая сторона (теорема 2), то АВ

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Видео:№237. Сравните стороны треугольника ABC, если: a) ∠A∠B∠C; б) ∠A∠B=∠C.Скачать

Пробный экзаменационный вариант «ОГЭ математика пробник 130 вариант» (2022)

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов

Сертификат и скидка на обучение каждому участнику

1. В таблице даны размеры (с точностью до мм) четырёх листов, имеющих форматы А0, А1, А3 и А4.

Установите соответствие между форматами и номерами листов. В ответ запишите последовательность четырёх цифр, соответствующих номерам листов, без пробелов, запятых и дополнительных символов.

Общепринятые форматы листов бумаги обозначают буквой А и цифрой: А0, А1, А2 и так далее. Лист формата А0 имеет форму прямоугольника, площадь которого равна 1 кв. м. Если лист формата А0 разрезать пополам параллельно меньшей стороне, получается два равных листа формата А1. Если лист А1 разрезать так же пополам, получается два листа формата А2.

Отношение большей стороны к меньшей стороне листа каждого формата одно и то же, поэтому листы всех форматов подобны. Это сделано специально для того, чтобы пропорции текста и его расположение на листе сохранялись при уменьшении или увеличении шрифта при изменении формата листа.

2. Сколько листов формата А3 получится из одного листа формата А2?

3. Найдите ширину листа бумаги формата А0. Ответ дайте в миллиметрах и округлите до ближайшего целого числа, кратного 10.

4. Найдите отношение длины меньшей стороны листа формата А3 к большей. Ответ округлите до десятых.

5. Бумагу формата А5 упаковали в пачки по 500 листов. Найдите массу пачки, если масса бумаги площади 1 кв. м равна 80 г. Ответ дайте в граммах.

6. Найдите значение выражения .

7. Известно, что число отрицательное. На каком из рисунков точки с координатами расположены на координатной прямой в правильном порядке?

В ответе укажите номер правильного варианта.

8. Найдите значение выражения

9. Найдите корень уравнения (x + 2)(− x + 6) = 0.

Если уравнение имеет более одного корня, в ответ запишите меньший из корней.

10. В фирме такси в данный момент свободно 30 машин: 6 чёрных, 3 жёлтые и 21 зелёная. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчику. Найдите вероятность того, что к нему приедет жёлтое такси

11. Установите соответствие между графиками функций и формулами, которые их задают.

Ответ укажите в виде последовательности цифр без пробелов и запятых в указанном порядке

12. Закон Кулона можно записать в виде где — сила взаимодействия зарядов (в ньютонах), и — величины зарядов (в кулонах), — коэффициент пропорциональности (в Н·м 2 /Кл 2 ), а — расстояние между зарядами (в метрах). Пользуясь формулой, найдите величину заряда (в кулонах), если Н·м 2 /Кл 2 , Кл, м, а Н.

13. Решите неравенство

В ответе укажите номер правильного варианта.

14. Улитка ползет от одного дерева до другого. Каждый день она проползает на одно и то же расстояние больше, чем в предыдущий день. Известно, что за первый и последний дни улитка проползла в общей сложности 9 метров. Определите, сколько дней улитка потратила на весь путь, если расстояние между деревьями равно 18 метрам.

15. Высота равностороннего треугольника равна . Найдите его периметр

16.

Касательные в точках A и B к окружности с центром O пересекаются под углом 18°. Найдите угол ABO. Ответ дайте в градусах.

17. Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH = 5 и HD = 15. Диагональ параллелограмма BD равна 17. Найдите площадь параллелограмма.

18. На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите её площадь.

19. Укажите номера верных утверждений.

1) Через любую точку проходит не менее одной прямой.

2) Если при пересечении двух прямых третьей прямой соответственные углы равны 65°, то эти две прямые параллельны.

3) Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы составляют в сумме 90°, то эти две прямые параллельны.

Если утверждений несколько, запишите их номера в порядке возрастания.

20. Решите уравнение

21. Дорога между пунктами A и В состоит из подъёма и спуска, а её длина равна 27 км. Турист прошёл путь из А в В за 8 часов, из которых спуск занял 3 часа. С какой скоростью турист шёл на спуске, если его скорость на подъёме меньше его скорости на спуске на 1 км/ч?

22. При каких значениях p вершины парабол и расположены по разные стороны от оси х?

23. Прямая AD, перпендикулярная медиане ВМ треугольника АВС, делит её пополам. Найдите сторону АС, если сторона АВ равна 4.

24. В параллелограмме АВСD проведены перпендикуляры ВЕ и DF к диагонали АС (см. рисунок). Докажите, что отрезки ВF и DЕ параллельны.

25. Медиана BM треугольника ABC является диаметром окружности, пересекающей сторону BC в её середине. Найдите этот диаметр, если диаметр описанной окружности треугольника ABC равен 8.

1. В таблице даны размеры (с точностью до мм) четырёх листов, имеющих форматы А0, А1, А3 и А4.

Пользуясь рисунком, можно сделать вывод, что формату А0 соответствует лист 3, формату А1 — лист 4, фомату А3 — лист 2, формату А4 — лист 1.

2. Сколько листов формата А3 получится из одного листа формата А2?

Исходя из рисунка, можно сделать вывод, что 2 листа формата А3 получится из одного листа формата А2.

Из таблицы, указанной в задании 1, можно сделать вывод, что ширина формата А0 равна 841 мм. Округляя, получаем ответ — 840 мм.

4. Найдите отношение длины меньшей стороны листа формата А3 к большей. Ответ округлите до десятых.

Из таблицы, указанной в задании 1, можно сделать вывод, что длина меньшей стороны формата А3 равна 297 мм, а большей стороны — 420 мм. Найдем отношение и округлим до десятых:

Большая сторона формата А5 совпадает с меньшей стороной формата А4, она равна 210 мм. Меньшую сторону формата А5 можно найти, разделив большую сторону формата А4 на 2: мм.

Площадь пятисот листов в 500 раз больше площади одного листа и равна

(мм 2 ).

Выразим ее в квадратных метрах:

(м 2 ).

Массу пачки можно найти, перемножив суммарную площадь на массу 1 кв. м.: г.

Приведём другое решение.

На листе формата А0 помещается 32 листа формата А5, поэтому площадь листа формата А5 в 32 раза меньше, чем площадь листа формата А0. Во столько же раз меньше вес. Следовательно, вес листа формата А5 равен грамма, а вес пачки равен граммов.

Ответ: 1243,2 или 1250.

Подробное пояснение приведено в задаче 408294 .

6. Найдите значение выражения .

Представим числа в стандартном виде:

В ответе укажите номер правильного варианта.

Поскольку , имеем: Поскольку имеем:

Правильный ответ указан под номером: 4.

8. Найдите значение выражения

Найдем значение выражения:

9. Найдите корень уравнения (x + 2)(− x + 6) = 0.

Если уравнение имеет более одного корня, в ответ запишите меньший из корней.

Вероятность того, что приедет желтая машина равна отношению количества желтых машин к общему количеству:

11. Установите соответствие между графиками функций и формулами, которые их задают.

Ответ укажите в виде последовательности цифр без пробелов и запятых в указанном порядке

Определим вид графика каждой из функций.

1) уравнение гиперболы.

2) уравнение параболы, ветви которой направленны вниз.

3) уравнение прямой.

4) уравнение верхней ветви параболы, направленной вправо.

Тем самым найдено соответствие: A — 3, Б — 1, В — 2.

Выразим заряд из закона Кулона:

13. Решите неравенство

В ответе укажите номер правильного варианта.

Правильный ответ указан под номером: 1.

Пусть улитка проползла в первый день метров, во второй — … , в последний — метров. Тогда м, а за дней проползла метров. Поскольку всего она проползла 18 метров, имеем: откуда Таким образом, улитка потратила на весь путь 4 дня.

15. Высота равностороннего треугольника равна . Найдите его периметр

Так как треугольник равносторонний, то его высота является и медианой, и биссектрисой. Тогда треугольник — прямоугольный. Тогда:

Таким образом, периметр равен

16.

Введём обозначение, как показано на рисунке. Касательные, проведённые к окружности из одной точки равны, поэтому следовательно, треугольник — равнобедренный. Откуда Угол между касательной и хордой равен половине дуги, которую он заключает, значит, дуга равна 162°. Угол AOB — центральный, поэтому он равен дуге, на которую опирается, следовательно, равен 162°. Рассмотрим треугольник AOB, он равнобедренный, следовательно,

Из прямоугольного треугольника по теореме Пифагора найдём

Площадь параллелограмма равна произведению основания на высоту:

18. На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите её площадь.

Площадь трапеции равна произведению полусуммы оснований на высоту. Таким образом,

19. Укажите номера верных утверждений.

1) Через любую точку проходит не менее одной прямой.

Если утверждений несколько, запишите их номера в порядке возрастания.

Проверим каждое из утверждений.

1) Через любую точку проходит бесконечное множество прямых, следовательно, утверждение 1 верно.

2) Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны — верно, это признак параллельности прямых. В утверждении сказано, что соответственные углы равны 65°, следовательно, они равны друг другу, тогда прямые параллельны.

3) Накрест лежащие углы двух параллельных прямых, пересечённых третьей, равны. Утверждение 3 неверно: если в сумме углы составляют 90°, то они могут быть не равны, и тогда прямые не будут параллельными.

20. Решите уравнение

Квадрат любого числа неотрицателен. Сумма двух неотрицательных чисел равна нулю, только если они оба равны нулю. Получаем систему уравнений:

Из первого уравнения или .
Из второго уравнения или .
Системе удовлетворяет единственное значение .

Пусть скорость, с которой турист спускался, равна х км/час, тогда его скорость на подъёме равна х − 1 км/ч, длина спуска равна 3х км, длина подъёма равна 5(х − 1) км. Поскольку весь путь равен 27 км, имеем: 3х + 5(х − 1) = 27, откуда х = 4 км/ч.

22. При каких значениях p вершины парабол и расположены по разные стороны от оси х?

Абсцисса вершины параболы определяется по формуле Для данных парабол это точки 4p и 3p.

Ордината вершины находится подстановкой в уравнение параболы. Для данных парабол получаем: и

Вершины парабол находятся по разные стороны от оси абсцисс, если ординаты их вершин имеют разные знаки.

Два множителя имеют разные знаки тогда и только тогда, когда их произведение отрицательно.

Тем самым, требуется решить неравенство

Заметим, что первый множитель больше нуля при всех значениях p, поэтому на него можно разделить. Имеем:

Произведение двух сомножителей больше нуля, если сомножители имеют одинаковый знак (см. рисунок). Таким образом, получаем ответ:

Ответ:

Координату параболы также можно найти по формуле

Рассмотрим треугольники и , они прямоугольные, катет — общий, равно следовательно, эти треугольники равны по двум катетам, значит, Вспомним, что — медиана:

— параллелограмм, поэтому стороны и равны. Углы и равны, как накрест лежащие при параллельных прямых и и секущей Рассмотрим треугольники и они прямоугольные, их гипотенузы равны и угол равен углу следовательно, эти треугольники равны по гипотенузе и углу, значит, равны отрезки и и следовательно, . Противоположные стороны четырёхугольника равны и параллельны, следовательно, этот четырёхугольник — параллелограмм, значит,

Введём обозначения, как показано на рисунке. Рассмотрим треугольник — он равнобедренный, следовательно, . Аналогично в треугольнике имеем: Теперь рассмотрим треугольник : сумма его углов равна 180°, поэтому

Поскольку кроме этого имеем:

Рассмотрим треугольники и они прямоугольные, имеют общий катет и равно следовательно, эти треугольники равны, а значит, .

Точка отстоит на равное расстояние от всех трёх вершин треугольника, , следовательно, точка — центр окружности, описанной около треугольника . Диаметр равен радиусу описанной окружности. Радиус описанной окружности

📸 Видео

№469. Стороны АВ и ВС треугольника ABC равны соответственно 16 см и 22 см, а высота,Скачать

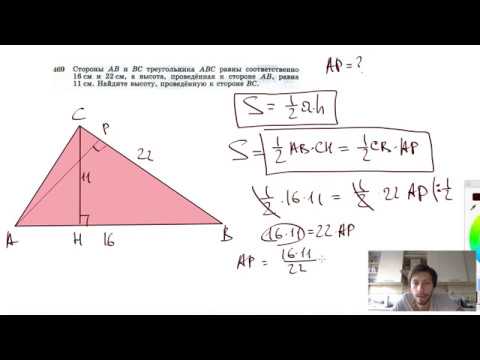
№762. Сторона равностороннего треугольника ABC равна а. Найдите: а) |AB+BC|Скачать

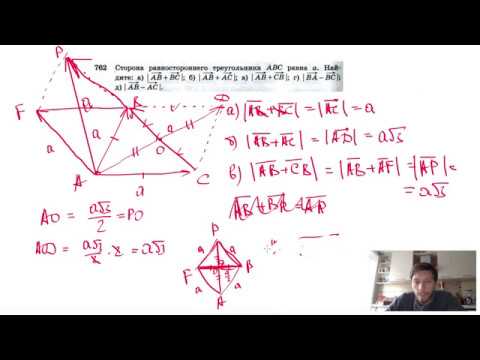
№90. Сторона AB треугольника ABC равна 17см, сторона АС вдвое больше стороны AB, а сторона ВССкачать

№768. Точки М и N — середины сторон АВ и АС треугольника ABC. Выразите векторыСкачать

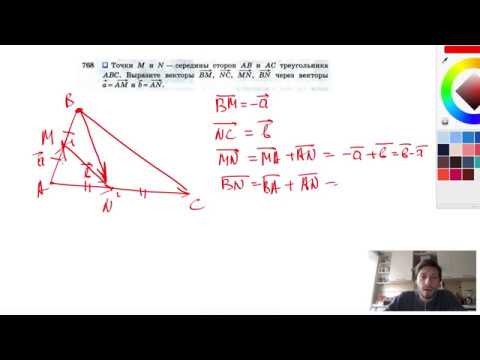
№566. Точки Р и Q — середины сторон АВ и АС треугольника ABC. Найдите периметр треугольникаСкачать

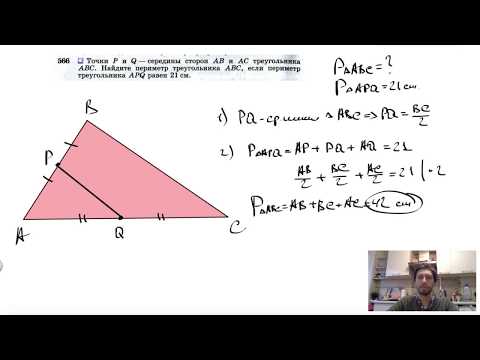
Геометрия Точки E и F являются соответственно серединами сторон AB и BC треугольника ABC. НайдитеСкачать

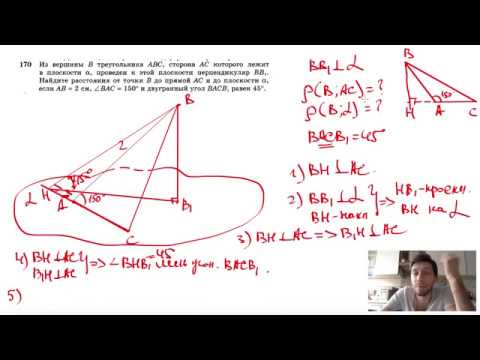
№170. Из вершины В треугольника ABC, сторона АС которого лежит в плоскости а, проведен к этойСкачать

Точки М и N являются серединами сторон АВ и ВС треугольника АВС. Площадь треугольника MBN равна 18.Скачать

В треугольнике ABC DE – средняя линия ... | ОГЭ 2017 | ЗАДАНИЕ 12 | ШКОЛА ПИФАГОРАСкачать

ОГЭ. Геометрия. Из открытого банка заданий ОГЭ (ФИПИ). Медианы №1Скачать

№942. Найдите медиану AM треугольника ABC, вершины которого имеют координаты: А(0; 1), В(1; -4)Скачать

№536. Отрезок BD является биссектрисой треугольника ABC. а) Найдите АВ, если ВС = 9 смСкачать

№537. Отрезок AD является биссектрисой треугольника ABC. Найдите BD и DC, если АВ = 14 смСкачать

Задание 3 ЕГЭ по математике. Урок 41Скачать

№258. Из середины D стороны ВС равностороннего треугольника ABC проведен перпендикулярСкачать

ЗАДАНИЕ 1|ЕГЭ ПРОФИЛЬ| Площадь треугольника ABC равна 52, DE-средняя линия, параллельная стороне AB.Скачать

1707 точка M и N являются серединами сторон AB и BC треугольника ABCСкачать

В треугольнике отмечены середины M и N сторон BC и AC ... | ОГЭ 2017 | ЗАДАНИЕ 12 | ШКОЛА ПИФАГОРАСкачать