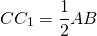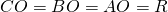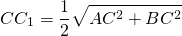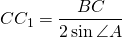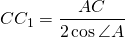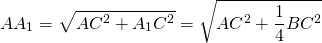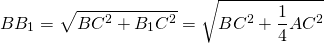Медиана в египетском треугольнике

Видео:8. Медиана треугольника и её свойства.Скачать

1.Теорема Пифагора

Теорема: В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Доказательство.

1. Разделим каждую сторону большого квадрата на два отрезка x и y точкой. И проведем через эти точки отрезки.

2. Тогда треугольники 1,2,3,4 равны по двум сторонам и углу между ними.

3. Т.к. сумма углов α + β = 90°, то фигура внутри большого квадрата тоже квадрат. (Все стороны = с и все углы = 90° )

4. Площадь большого квадрата равна сумме площадей малого квадрата и 4-х треугольников. (Рис.1)

Рис.1 Теорема Пифагора.

Видео:Построение медианы в треугольникеСкачать

2.Египетский треугольник

Пусть дан треугольник со сторонами АВ = a, ВС = b, АС = c. При условии, что а 2 + b 2 = с 2 . Доказать, что угол, лежащий против стороны с, прямой.

Допустим, что треугольник АВС не прямоугольный. Тогда можно опустить высоту на сторону АС — h (Рис.2). Из двух прямоугольных треугольников ABD и DBC составим следующую систему уравнений по теореме Пифагора. Обозначим AD как х, BD — высота h.

Но по условию задачи а 2 + b 2 = с 2 . Следовательно х = 0 и сторона а = h. Т.е. угол между сторонами АВ и АС — прямой.

В древнем Египте данное соотношение применялось очень широко. Например для построения прямого угла между сторонами при строительстве зданий и сооружений. Или при измерении прямых углов пахотных земель. Так как зная соотношение, можно легко построить прямой угол. По этой причине треугольник со сторонами 3,4,5 ед. называют Египетским треугольником.

Рис.2 Египетский треугольник.

Видео:🔥 Свойства МЕДИАНЫ #shortsСкачать

3.Соотношение между углами и сторонами в прямоугольном треугольнике

Пусть дан прямоугольный треугольник АВС. Проведем прямую ЕF параллельную стороне АВ (Рис.3). Тогда по теореме о пропорциональных отрезках:

Т.е. соs α не зависит от размеров прямоугольного треугольника, а зависит только от величины угла. Тогда по теореме Пифагора sin α также зависит только от величины угла. А следовательно tg α и ctg α.

Отсюда можно сделать следующие выводы:

AB = BC sin α
AC = BC cos α
AB = AC tg α
AC = AB ctg α

Рис.3 Соотношение между углами и сторонами в прямоугольном треугольнике.

Видео:Высота, биссектриса, медиана. 7 класс.Скачать

4.Основные тригонометрические тождества

Пусть дан прямоугольный треугольник со сторонами a,b,c. (Рис.4)

Рис.4 Основные тригонометрические тождества.

Репетитор: Васильев Алексей Александрович

Предметы: математика, физика, информатика, экономика, программирование.

2000 руб / 120 мин — подготовка к ЕГЭ и ГИА для школьников. 3000 руб / 120 мин — индивидуально (базовый уровень). 2000 руб / 120 мин — студенты.

Тел. 8 916 461-50-69, email: alexey-it@ya.ru

5.Пример 1

У треугольника одна сторона равна 1 м, а прилегающие к ней углы 30° и 45°. Найдите другие стороны треугольника. (рис.5)

Так как один из углов 30 градусов, то катет, лежащий против этого угла равен половине гипотенузы, т.е. h = b/2. А следовательно КС = h, т.к. угол β = 45 градусов.

Рис.5 Задача. У треугольника одна сторона равна 1 м.

Пример 2

Найдите высоту равнобокой трапеции, если ее основания равны 6 м и 12 м, а боковая сторона равна 5 м. (Рис.6)

Решение:

Пусть ABCD данная трапеция. ВЕ перпендикуляр, опущенный на основание AD. Тогда АЕ = (12 — 6)/ 2 = 3 м. Так как АЕ = FD.

По теореме Пифагора:

АВ 2 = AE 2 + BE 2

Рис.6 Задача. Найдите высоту равнобокой трапеции.

Пример 3

Докажите, что расстояние между двумя точками на сторонах треугольника не больше большей из его сторон. (Рис.7)

Доказательство:

Пусть ABC данный треугольник. АС — его большая сторона. Проведем отрезок DE параллельно стороне АС. Необходимо доказать, что отрезок DE меньше стороны АС. Если мы докажем, что отрезок DE меньше большей стороны АС, то при взятии двух других точек треугольника на других его меньших сторонах, отрезок между этими точками будет также меньше стороны АС.

Опустим перпендикуляр BF на большую сторону АС. Составим следующее соотношение:

АС = АВ сos α + ВС cos β

Тогда отрезок DE будет равен:

DE = DB сos α + ВE cos β

Так как DB Рис.7 Задача. Докажите, что расстояние между двумя точками.

Пример 4

Докажите, что прямая, отстоящая от центра окружности на расстояние меньше радиуса, пересекает окружность в двух точках. (Рис.8)

Доказательство:

Пусть дана окружность с центром в точке О. И прямая а, отстоящая от центра окружности точки О, на расстояние ОЕ = h h, то прямая а будет иметь две точки пересечения. Так как

h = ОА*cos α = ОВ*cos (-α)

Радиусы ОА и ОВ можно рассматривать как две наклонные, отложенные в двух полуплоскостях, в треугольнике АОВ перпендикуляра ОЕ.

Рис.8 Задача. Докажите, что прямая, отстоящая от центра окружности.

Пример 5

Даны три положительных числа a,b,c. Докажите, что если каждое из этих чисел меньше суммы двух других, то существует треугольник со сторонами a,b,c. (Рис.9)

Доказательство:

Пусть даны три точки. Если эти три точки лежат на одной прямой, например А,Е,С, то расстояния между этими точками связаны соотношением: АС = АЕ + ЕС

Отсюда видно, что каждое из трех расстояний не больше двух других. Т.е. расстояние между точками А и С не больше двух расстояний АЕ и ЕС.

Если взять три точки, не лежащих на одной прямой, например А,В,С и опустить перпендикуляр ВЕ, то АС AB + BC (Рис.9 б). Тогда концы отрезков АВ и СВ не смогут совпасть в точке В. Так как, если даже отрезки такой же длины отложить на отрезке АС, то получится, что

Таким образом, если числа a,b и с принять за длины отрезков, то концы отрезков АВ и СВ не смогут совпасть в одной точке В. Между ними образуется некое расстояние ВВ₁ и построить треугольник не получится.

Рис.9 Задача. Даны три положительных числа.

Видео:Свойство медианы в прямоугольном треугольнике. 8 класс.Скачать

Все формулы медианы прямоугольного треугольника

Медиана, отрезок |CO|, исходящий из вершины прямого угла BCA и делящий гипотенузу c , пополам.

Медиана в прямоугольном треугольнике ( M ), равна, радиусу описанной окружности ( R ).

M — медиана

R — радиус описанной окружности

O — центр описанной окружности

с — гипотенуза

a, b — катеты

α — острый угол CAB

Медиана равна радиусу и половине гипотенузы, ( M ):

Формула длины через катеты, ( M ):

Формула длины через катет и острый угол, ( M ):

Видео:Медиана прямоугольного треугольника— Геометрия ОГЭСкачать

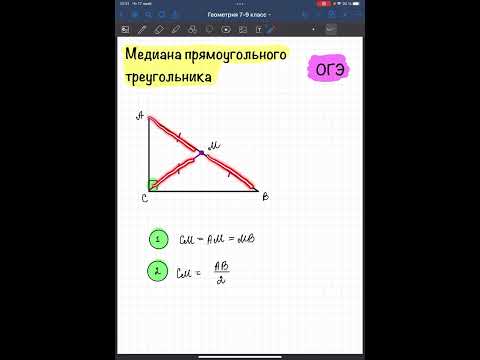
Медиана в прямоугольном треугольнике

Медиана в прямоугольном треугольнике — это отрезок, который соединяет вершину треугольника и середину противоположной стороны, то есть вершину острого угла с серединой противолежащего катета или вершину прямого угла с серединой гипотенузы.

Все медианы прямоугольного треугольника пересекаются в одной точке и делятся этой точкой в отношении два к одному, считая от вершины:

Из всех медиан прямоугольного треугольника в задачах чаще всего речь идет о медиане, проведенной к гипотенузе. Это связано с ее свойствами.

Свойства медианы, проведенной к гипотенузе:

1) Медиана, проведенная к гипотенузе, равна половине гипотенузы.

(в следующий раз рассмотрим доказательство этого свойства)

2) Медиана, проведенная к гипотенузе, равна радиусу описанной около прямоугольного треугольника окружности.

Пользуясь свойствами прямоугольного треугольника, длины медиан прямоугольного треугольника можно выразить через катеты и острые углы.

Например:

Видео:Задание 15 ОГЭ. Медиана равностороннего треугольникаСкачать

12 Comments

Информация очень хорошая. Правда не помогла мне решить задачу, которую мой сын не решил на контрольной. приведу условие:
Из прямого угла треугольника проведена медиана на гипотенузу. Длина медианы 6см. Определить катеты.

Петр, данных для определения катетов недостаточно. Длина гипотенузы в 2 раза больше длины медианы — 12 см. Это всё, что можно сказать по данным условия.

не правда надо провести высоту из прямого угла дальше все получится. один катет равен 6 а второй 2 корня из 22

Сумма квадратов катетов равна квадрату гипотенузы. Проверим 6^2+(2*корень из 22)^2
=36+4*22=36+88=124. Квадрат гипотенузы 12^2=144

попробуйте составить уравнение,обозначив 1 из катетов через х а 2-ой катет обозначьте буквами…x^2+BC^2=12^2…да числа не очень,но это 1 способ..решаю дальше:BC^2=12^2-x^2
BC^2=11x
X^2+11X=144
X^2=12
x(1 катет)=корню из 12,а «-ой катет=11 корней из 12….решал на основе теоремы пифагора

задача имеет бесконечное кол-во решений. решение возможно только в виде формулы или графика, где описана зависимость между катетами и гипотенузой

Да просто треугольник медианой делится на два треугольника с одинаковыми катетами, а дальше как уже предлагалось выше Пифагор во спасение))

А кто вам сказал, что медиана в прямоугольном треугольнике является еще и высотой? Откуда у вас два треугольника с одинаковыми катетами?

Спасибо за понятное объяснение, но у нас задача немного другая.
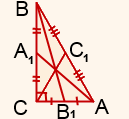
В прямоугольном треугольнике АВС угол С= 90 градусов,медиана ВВ1 равна 10 см.Найдите медианы АА1 СС1, если известно, что АС=12 см.( используя т.Пифагора.

1) Рассмотрим треугольник BB1C. В нём угол С равен 90 градусов, BB1=10 см, B1C=6 см (так как BB1 — медиана). По теореме Пифагора находим BC: BC=8 см. 2) Рассмотрим треугольник AA1C. В нём угол С равен 90 градусов, AC=12 см, AA1=4 см (так как BB1 — медиана). По теореме Пифагора находим AA1: AA1=4√10 см.3) Из треугольника ABC по теореме Пифагора найдём AB: AB=4√13 см. 4) CC1=1/2 AB (как медиана, проведённая к гипотенузе), CC1=2√13 см.
Где-то так.

🎦 Видео

Все свойства медианы в одной задаче.Скачать

Длина медианы треугольникаСкачать

7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

Все факты о медиане треугольника для ЕГЭСкачать

Найдите площадь треугольника, если его медианы равны 3, 4 и 5Скачать

Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать

ГЕОМЕТРИЯ 7 класс. Медиана прямоугольного треугольника. Свойство. Доказательство для 7 класса.Скачать

Замечательные точки треугольника | Ботай со мной #030 | Борис Трушин ||Скачать

Формулы для медианы треугольникаСкачать

Медиана треугольника. Построение. Свойства.Скачать

Сумма углов треугольника. Геометрия 7 класс | МатематикаСкачать

Задача, которую исключили из экзамена в АмерикеСкачать

Свойство медианы проведенной к гипотенузе.Скачать