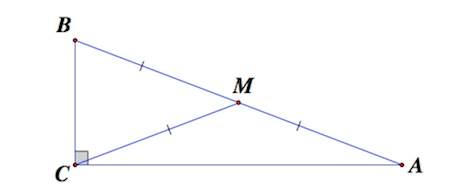
Докажем, что если в треугольнике медиана равна половине стороны, то этот треугольник — прямоугольный.
Если медиана треугольника равна половине стороны, к которой она проведена, то угол напротив этой стороны равен 90º.
1) Так как CO — медиана треугольника ABC и CO=1/2 AB (по условию), то CO=AO=BO.
Поэтому, треугольник AOC — равнобедренный с основанием AC,
треугольник BOC — равнобедренный с основанием BC (по определению равнобедренного треугольника).

Так как сумма углов треугольника равна 180º, то в треугольнике AOC
Видео:Доказать, что медиана, проведенная к гипотенузе, равна половине гипотенузыСкачать

Элементы треугольника. Медиана
Видео:Если медиана равна половине стороныСкачать

Определение
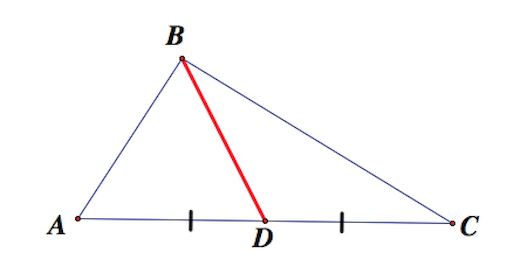
Медианой треугольника называют отрезок, соединяющий вершину треугольника с серединой противоположной стороны
Видео:№231. Медиана AM треугольника ABC равна половине стороны ВС. Докажите, что треугольникСкачать

Свойства
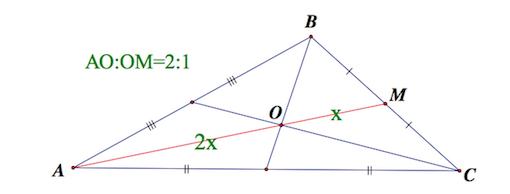
1. Медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2:1, считая от вершины . Эта точка называется центром тяжести треугольника.
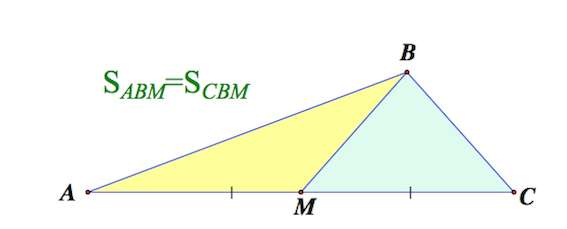
2. Медиана треугольника делит его на два треугольника равной площади (равновеликих треугольника)
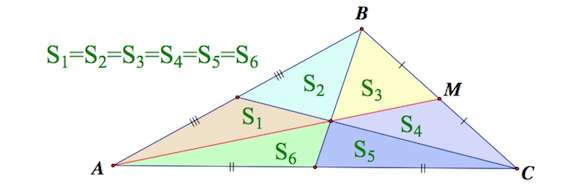
3. Медианы треугольника делят треугольник на 6 равновеликих треугольников
4. Медиана, проведенная к гипотенузе прямоугольного треугольника, равна половине гипотенузы
5. Длина медианы треугольника вычисляется по формуле:
, где где
— медиана к стороне
;
— стороны треугольника
6. Длина стороны треугольника через медианы вычисляется по формуле:
, где
– медианы к соответствующим сторонам треугольника,
— стороны треугольника.
Чтобы не потерять страничку, вы можете сохранить ее у себя:
Видео:Свойство медианы в прямоугольном треугольнике. 8 класс.Скачать

Свойства прямоугольного треугольника
| Фигура | Рисунок | Формулировка | ||||||||
| Прямоугольный треугольник | ||||||||||
| Равнобедренный прямоугольный треугольник | ||||||||||
| Прямоугольный треугольник с углом в 30° |
| Прямоугольный треугольник |
| Равнобедренный прямоугольный треугольник |
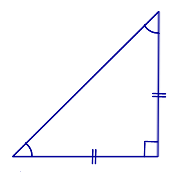 Определение равнобедренного прямоугольного треугольника: Равнобедренным прямоугольным треугольником называют такой прямоугольный треугольник, у которого равны катеты. Свойство углов прямоугольного треугольника: Острые углы равнобедренного прямоугольного треугольника равны 45° . |
| Прямоугольный треугольник с углом в 30° |
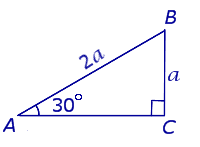 Свойство прямоугольного треугольника с углом в 30° : Катет прямоугольного треугольника, лежащий против угла в 30° , равен половине гипотенузы. Признак прямоугольного треугольника с углом в 30° : Если в прямоугольном треугольнике один из катетов равен половине гипотенузы, то этот катет лежит против угла в 30° . |
| Медиана, проведённая к гипотенузе прямоугольного треугольника |
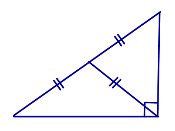 Свойство медианы, проведенной к гипотенузе прямоугольного треугольника: Медиана прямоугольного треугольника, проведённая из вершины прямого угла, равна половине гипотенузы. Признак прямоугольного треугольника: Если в треугольнике медиана равна половине стороны, к которой она проведена, то такой треугольник является прямоугольным. |
| Центр описанной окружности |
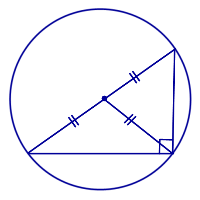 Свойство окружности, описанной около прямоугольного треугольника: Середина гипотенузы прямоугольного треугольника является центром описанной около него окружности. Признак прямоугольного треугольника: Если в треугольнике центр описанной окружности лежит на одной из сторон, то этот треугольник является прямоугольным треугольником, а центр описанной окружности совпадает с серединой гипотенузы. |
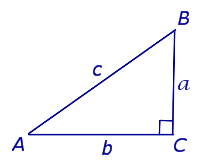 В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов Обратная теорема Пифагора: Если в треугольнике квадрат одной стороны равен сумме квадратов двух других сторон, то такой треугольник является прямоугольным 📺 Видео8. Медиана треугольника и её свойства.Скачать  Высота, биссектриса, медиана. 7 класс.Скачать  Уравнения стороны треугольника и медианыСкачать  ГЕОМЕТРИЯ 7 класс. Медиана прямоугольного треугольника. Свойство. Доказательство для 7 класса.Скачать  Задание 15 ОГЭ. Медиана равностороннего треугольникаСкачать  Медиана в прямоугольном треугольникеСкачать  7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать  №404. Докажите, что медиана прямоугольного треугольника, проведенная к гипотенузеСкачать  7 кл г. Теорема: «катет лежавший напротив угла в 30 градусов равен половине гипотенузы»Скачать  🔥 Свойства МЕДИАНЫ #shortsСкачать  Длина медианы треугольникаСкачать  Геометрия 8 Класс Урок 4 Удвоение медианыСкачать  ОГЭ Задание 25 Свойство медиан прямоугольного треугольникаСкачать  Медиана в прямоугольном треугольникеСкачать  Формулы для медианы треугольникаСкачать  Задача за секунду. ОГЭ геметрия. Медиана прямоугольного треугольникаСкачать  |