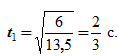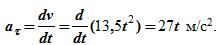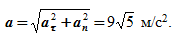Пример решения задачи по определению нормального, касательного и модуля полного ускорения точки, а также, угла с вектором скорости, точки, движущейся по окружности заданного радиуса и известному закону заданному уравнением.
Видео:Движение тела по окружности с постоянной по модулю скоростью | Физика 9 класс #18 | ИнфоурокСкачать
Задача
Точка движется по окружности радиуса R=4 м, закон ее движения определяется уравнением s=4,5t 3 ( s в метрах, t в секундах).
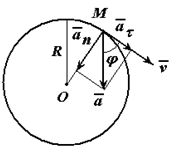
Определить модуль полного ускорения и угол φ его с вектором скорости в тот момент t1, когда скорость будет равна 6 м/с (рисунок 1.6).
Видео:Центростремительное ускорение. 9 класс.Скачать
Решение
Дифференцируя s по времени, находим модуль вектора скорости точки
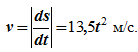
Подставляя в это выражение значение скорости, получим 6=13,5t1 2 , откуда находим
Касательное ускорение для любого момента времени равно
Так как для окружности радиус кривизны ρ=R, то нормальное ускорение для любого момента времени равно
Модуль вектора полного ускорения точки равен
Угол между вектором полного ускорения и вектором скорости определим следующим образом:
Видео:Физика - движение по окружностиСкачать
Кинематика поступательного движения
Автомобиль движется с постоянной по модулю скоростью по траектории, представленной на рисунке. В какой из указанных точек траектории центростремительное ускорение максимально?
 |
#1 #2 #3 #Во всех точках одинаково
Точка М движется по спирали в направлении, указанном стрелкой. Нормальное ускорение по величине не изменяется. При этом величина скорости …
# уменьшается # увеличивается # не изменяется
Точка М движется по спирали с постоянной по величине скоростью в направлении, указанном стрелкой. При этом величина нормального ускорения …
# уменьшается # увеличивается # не изменяется
Точка М движется по спирали в направлении, указанном стрелкой. Нормальное ускорение по величине не изменяется. При этом величина скорости …
# уменьшается # увеличивается # не изменяется
Точка М движется по спирали в направлении, указанном стрелкой. Нормальное ускорение по величине не изменяется. При этом величина скорости …
# увеличивается # уменьшается # не изменяется
Точка М движется по окружности с постоянным тангенциальным ускорением. Если проекция тангенциального ускорения на направление скорости положительна, то величина нормального ускорения…
# увеличивается # уменьшается # не изменяется
Точка М движется по окружности с постоянным тангенциальным ускорением. Если проекция тангенциального ускорения на направление скорости отрицательна, то величина нормального ускорения…
# уменьшается # увеличивается # не изменяется
Материальная точка M движется по окружности со скоростью 
. На рис. 1 показан график зависимости Vτ от времени ( 
– единичный вектор положительного направления, Vτ – проекция на это направление). На рис. 2 укажите направление ускорения т.М в момент времени t2.
Материальная точка M движется по окружности со скоростью . На рис. 1 показан график зависимости Vτ от времени ( – единичный вектор положительного направления, Vτ – проекция на это направление). На рис. 2 укажите направление ускорения т.М в момент времени t1.
Материальная точка M движется по окружности со скоростью . На рис. 1 показан график зависимости Vτ от времени ( – единичный вектор положительного направления, Vτ – проекция на это направление). На рис. 2 укажите направление ускорения т.М в момент времени t2.
Материальная точка M движется по окружности со скоростью . На рис. 1 показан график зависимости Vτ от времени ( – единичный вектор положительного направления, Vτ – проекция на это направление). На рис. 2 укажите направление ускорения т.М в момент времени t3.
Материальная точка M движется по окружности со скоростью . На рис. 1 показан график зависимости Vτ от времени ( – единичный вектор положительного направления, Vτ – проекция на это направление). На рис. 2 укажите направление ускорения т.М в момент времени t1.
Материальная точка M движется по окружности со скоростью . На рис. 1 показан график зависимости Vτ от времени ( – единичный вектор положительного направления, Vτ – проекция на это направление). На рис. 2 укажите направление ускорения т.М в момент времени t3.
Если at и an – тангенциальная и нормальная составляющие ускорения, то для равномерного движения по окружности справедливы соотношения:
Если at и an – тангенциальная и нормальная составляющие ускорения, то соотношения: at = a = const, an = 0 справедливы для.
#прямолинейного равноускоренного движения #прямолинейного равномерного движения #равномерного криволинейного движения #равномерного движения по окружности
Если at и an – тангенциальная и нормальная составляющие ускорения, то соотношения: at = 0, an = const справедливы для.
#равномерного криволинейного движения #прямолинейного равноускоренного движения #прямолинейного равномерного движения #равномерного движения по окружности
Два тела брошены под одним и тем же углом к горизонту с начальными скоростями V0и 2V0. Если сопротивлением воздуха пренебречь, то соотношение дальностей полета S2/S1 равно .
Материальная точка М движется по окружности со скоростью 
. На рис. 1 показан график зависимости проекции скорости 
от времени ( 
– единичный вектор положительного направления, – проекция на это направление). При этом для нормального an и тангенциального at ускорения выполняются условия.
# 
– увеличивается, 
– постоянно # – постоянно, – увеличивается # – увеличивается, – увеличивается # – постоянно, – постоянно
Камень бросили под углом к горизонту соскоростью V0. Его траектория в однородном поле тяжести изображена на рисунке. Сопротивления воздуха нет.
Модуль тангенциального ускорения at на участке А-В-С…
# увеличится # не изменяется # уменьшается
Автомобиль движется с постоянной по величине скоростью по траектории, представленной на рисунке. В какой из указанных точек траектории полное ускорение минимально?
| |
#1 #2 #3 #Во всех точках одинаково
Тело брошено с поверхности Земли со скоростью 20 м/с под углом 45° к горизонту. Определите радиус кривизны его траектории в верхней точке. Сопротивлением воздуха пренебречь. (g = 10 м/с 2 ).
#10 м #20 м #30 м #80 м
Графики зависимости величины тангенциального ускорения от времени для равномерного движения тела по окружности изображен на рисунке.
# 
# 
# 
# 
Точка М движется по спирали с постоянным по величине нормальным ускорением в направлении, указанном стрелкой. При этом проекция тангенциального ускорения на направление скорости .
#равна нулю #меньше нуля #больше нуля
Материальная точка М движется по окружности со скоростью . На рис. 1 показан график зависимости проекции скорости от времени ( – единичный вектор положительного направления, – проекция на это направление). При этом для нормального an и тангенциального at ускорения выполняются условия.
# > 0; = 0 # = 0; 0; > 0 # > 0; aB # aA = aB = 0 # aA = aB ≠ 0.
Тело брошено с поверхности Земли со скоростью 20 м/с под углом 60° к горизонту. Определите радиус кривизны его траектории в верхней точке. Сопротивлением воздуха пренебречь. (g = 10 м/с 2 ).
#10 м #20 м #30 м #80 м
Материальная точка движется по окружности. На чертеже изображена зависимость ее скорости от времени. Точка имеет наибольшее тангенциальное ускорение в момент времени .
Тело брошено под углом к горизонту и движется в поле силы тяжести Земли. На рисунке изображен восходящий участок траектории данного тела.
Правильно изображает полное ускорение вектор .
Тело брошено с поверхности Земли со скоростью 20 м/с под углом 30° к горизонту. Определите радиус кривизны его траектории в верхней точке. Сопротивлением воздуха пренебречь. (g = 10 м/с 2 ).
#10 м #20 м #30 м #80 м
Тангенциальное ускорение точки меняется согласно графику.
Такому движению соответствует зависимость скорости от времени .
# 
# 
# 
# 
.
Видео:Урок 47. Неравномерное движение по окружности. Тангенциальное ускорениеСкачать
Материальная точка м движется по окружности вектор полного ускорения
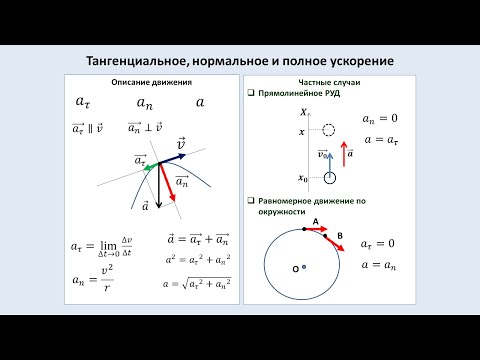
тангенциальное нормальное полное ускорения
Колесо с радиусом 0,1 м вращается так, что зависимость угла поворота радиуса колеса от времени дается уравнением φ = 5+t+2t 2 +t 3 рад. Для точек, лежащих на ободе колеса, определить угловую скорость, угловое, нормальное, тангенциальное и полное ускорения к концу второй секунды. Какой угол образует вектор полного ускорения и вектор линейной скорости?
Материальная точка движется по окружности радиуса 1 м согласно уравнению s = 8t – 0,2t 3 . Найти скорость, тангенциальное, нормальное и полное ускорение в момент времени 3 с.
Колесо радиусом 0,3 м вращается согласно уравнению φ = 5–2t+0,3t 2 . Найти нормальное, тангенциальное и полное ускорение точек на ободе колеса через 5 с после начала движения.
Шарик массы т = 100 г, подвешенный на нити, отвели в сторону так, что нить образовала прямой угол с вертикалью, а затем отпустили. Найти: 1) тангенциальное, нормальное и полное ускорение и натяжение нити в зависимости от угла θ отклонения нити от вертикали; 2) натяжение нити в тот момент, когда вертикальная составляющая скорости шарика максимальна.
Используя данные предыдущей задачи, определить: 1) частоту вращения диска в момент времени t2 в об/с и об/мин; 2) в момент времени t2 определить скорость, нормальное, тангенциальное и полное ускорение точек, находящихся на расстоянии 10 см от оси вращения.
Данные из предыдущей задачи: t2 = 15 с; ω(t2) = 11,8 рад/с; β(t2) = 1,1 рад/с 2 .
Предыдущая задача: Диск вращается согласно уравнению φ = а + bt + ct 2 + dt 3 , где φ — угол поворота радиуса в радианах, t — время в секундах. Определить угловую скорость и ускорение в моменты времени t1 = 11 с и t2 = 15 с. Каковы средние значения угловой скорости и углового ускорения в промежутке времени от t1 = 11 до t2 = 15 с включительно, если для Вашего варианта а = 1, b = 2 с –1 , с = 0,1 с –2 , d = 0,01 с –3 ?
Точка движется по кругу так, что зависимость пути от времени задается уравнением: S = А + Bt +Ct 2 , где В = –2 м/с и С = 1 м/с 2 . Найти линейную скорость точки, ее тангенциальное, нормальное и полное ускорение через 3 с после начала движения, если известно, что нормальное ускорение в момент времени 2 с составляет 0,5 м/с 2 .
Найти нормальное, тангенциальное и полное ускорение электрона на произвольной стационарной орбите в ионе Не+.
Движение точки по окружности радиуса R = 4 м задано уравнением: S = A+Bt+Ct 2 . Определить тангенциальное, нормальное и полное ускорение точки в момент времени t = 2 с, если А = 10 м, В = –2 м/с и С = 1 м/с 2 .
Автомобиль движется по закруглению шоссе, имеющему радиус кривизны 50 м. Длина пути автомобиля выражается уравнением S = 10+10t+0,5t 2 (путь — в метрах, время — в секундах). Найти скорость автомобиля, его тангенциальное, нормальное и полное ускорения через 5 с после начала движения.
Материальная точка движется по окружности радиуса 80 см по закону S = 10t–0,1t 3 (путь в метрах, время в секундах). Найти скорость, тангенциальное, нормальное и полное ускорения через 2 с после начала движения.
Материальная точка движется по окружности диаметром 40 м. Зависимость ее координаты от времени движения определяется уравнением S = t 3 +4t 2 –3t+8. В какой момент точка изменяет направление движения? Определить пройденный путь, скорость, нормальное, тангенциальное и полное ускорение движущейся точки через 4 с после начала движения.
Тело движется по криволинейной траектории. Пройденный путь меняется со временем по закону s = 2 + 0,5t 2 , м. Определить нормальное, тангенциальное и полное ускорение при t = 1 с. Радиус кривизны траектории движения в этот момент времени равен 50 см. Какова средняя скорость за 1 с движения?
Материальная точка начала вращаться с постоянным угловым ускорением из положения 1 и через 0,1 с оказалась в положении 2. Найти угловые ускорение и скорость в точке 2. Указать направления тангенциального, нормального и полного ускорений, а также линейной и угловой скоростей для положения 2.
Движение точки по окружности радиусом R = 2 м задано уравнением φ = A+Bt+Ct 2 , где А = 10 м, В = –3 м/с, С = 2 м/с 2 . Найти тангенциальное, нормальное и полное ускорения точки в момент времени t = 2 с.
📸 Видео
Криволинейное, равномерное движение материальной точки по окружности. 9 класс.Скачать
Рассмотрение темы: "Тангенциальное, нормальное и полное ускорение"Скачать
Равномерное движение точки по окружности | Физика 10 класс #7 | ИнфоурокСкачать
Движение материальной точки по окружности | Физика ЕГЭ, ЦТСкачать
Физика 10 класс (Урок№4 - Равномерное движение точки по окружности.)Скачать
Лекция 6.5 | Нормальное и тангенциальное ускорение | Александр Чирцов | ЛекториумСкачать
УСКОРЕНИЕ - Что такое равноускоренное движение? Как найти ускорение // Урок Физики 9 классСкачать
Движение по окружности. Нормальное и тангенциальное ускорение | 50 уроков физики (4/50)Скачать
Урок 43. Криволинейное движение. Равномерное движение по окружности. Центростремительное ускорениеСкачать
ФИЗИКА 10 класс : Механическое движение | Материальная точка, траектория, перемещение.Скачать
Задача о полном ускорении при неравномерном движении тела по окружности.Скачать
Физика | Равномерное движение по окружностиСкачать
Скорости и ускорения точек вращающегося телаСкачать
КРИВОЛИНЕЙНОЕ ДВИЖЕНИЕ - Угловое Перемещение, Угловая Скорость, Центростремительное УскорениеСкачать
Лекция №1 "Кинематика материальной точки" (Булыгин В.С.)Скачать
Кинематика точки Движение по окружностиСкачать
