Материальная точка движется по окружности с нормальным ускорением

тангенциальное нормальное полное ускорения

Колесо с радиусом 0,1 м вращается так, что зависимость угла поворота радиуса колеса от времени дается уравнением φ = 5+t+2t 2 +t 3 рад. Для точек, лежащих на ободе колеса, определить угловую скорость, угловое, нормальное, тангенциальное и полное ускорения к концу второй секунды. Какой угол образует вектор полного ускорения и вектор линейной скорости?

Материальная точка движется по окружности радиуса 1 м согласно уравнению s = 8t – 0,2t 3 . Найти скорость, тангенциальное, нормальное и полное ускорение в момент времени 3 с.

Колесо радиусом 0,3 м вращается согласно уравнению φ = 5–2t+0,3t 2 . Найти нормальное, тангенциальное и полное ускорение точек на ободе колеса через 5 с после начала движения.

Шарик массы т = 100 г, подвешенный на нити, отвели в сторону так, что нить образовала прямой угол с вертикалью, а затем отпустили. Найти: 1) тангенциальное, нормальное и полное ускорение и натяжение нити в зависимости от угла θ отклонения нити от вертикали; 2) натяжение нити в тот момент, когда вертикальная составляющая скорости шарика максимальна.

Используя данные предыдущей задачи, определить: 1) частоту вращения диска в момент времени t₂ в об/с и об/мин; 2) в момент времени t₂ определить скорость, нормальное, тангенциальное и полное ускорение точек, находящихся на расстоянии 10 см от оси вращения.
Данные из предыдущей задачи: t₂ = 15 с; ω(t₂) = 11,8 рад/с; β(t₂) = 1,1 рад/с 2 .
Предыдущая задача: Диск вращается согласно уравнению φ = а + bt + ct 2 + dt 3 , где φ — угол поворота радиуса в радианах, t — время в секундах. Определить угловую скорость и ускорение в моменты времени t₁ = 11 с и t₂ = 15 с. Каковы средние значения угловой скорости и углового ускорения в промежутке времени от t₁ = 11 до t₂ = 15 с включительно, если для Вашего варианта а = 1, b = 2 с –1 , с = 0,1 с –2 , d = 0,01 с –3 ?

Точка движется по кругу так, что зависимость пути от времени задается уравнением: S = А + Bt +Ct 2 , где В = –2 м/с и С = 1 м/с 2 . Найти линейную скорость точки, ее тангенциальное, нормальное и полное ускорение через 3 с после начала движения, если известно, что нормальное ускорение в момент времени 2 с составляет 0,5 м/с 2 .

Найти нормальное, тангенциальное и полное ускорение электрона на произвольной стационарной орбите в ионе Не+.

Движение точки по окружности радиуса R = 4 м задано уравнением: S = A+Bt+Ct 2 . Определить тангенциальное, нормальное и полное ускорение точки в момент времени t = 2 с, если А = 10 м, В = –2 м/с и С = 1 м/с 2 .

Автомобиль движется по закруглению шоссе, имеющему радиус кривизны 50 м. Длина пути автомобиля выражается уравнением S = 10+10t+0,5t 2 (путь — в метрах, время — в секундах). Найти скорость автомобиля, его тангенциальное, нормальное и полное ускорения через 5 с после начала движения.

Материальная точка движется по окружности радиуса 80 см по закону S = 10t–0,1t 3 (путь в метрах, время в секундах). Найти скорость, тангенциальное, нормальное и полное ускорения через 2 с после начала движения.

Материальная точка движется по окружности диаметром 40 м. Зависимость ее координаты от времени движения определяется уравнением S = t 3 +4t 2 –3t+8. В какой момент точка изменяет направление движения? Определить пройденный путь, скорость, нормальное, тангенциальное и полное ускорение движущейся точки через 4 с после начала движения.

Тело движется по криволинейной траектории. Пройденный путь меняется со временем по закону s = 2 + 0,5t 2 , м. Определить нормальное, тангенциальное и полное ускорение при t = 1 с. Радиус кривизны траектории движения в этот момент времени равен 50 см. Какова средняя скорость за 1 с движения?

Материальная точка начала вращаться с постоянным угловым ускорением из положения 1 и через 0,1 с оказалась в положении 2. Найти угловые ускорение и скорость в точке 2. Указать направления тангенциального, нормального и полного ускорений, а также линейной и угловой скоростей для положения 2.

Движение точки по окружности радиусом R = 2 м задано уравнением φ = A+Bt+Ct 2 , где А = 10 м, В = –3 м/с, С = 2 м/с 2 . Найти тангенциальное, нормальное и полное ускорения точки в момент времени t = 2 с.

Видео:Урок 47. Неравномерное движение по окружности. Тангенциальное ускорениеСкачать

Материальная точка движется по окружности с нормальным ускорением

Маленький шарик, подвешенный на нити, вращается в горизонтальной плоскости. Найти отношение моментов инерции шарика `I_1//I_2` относительно оси, проходящей через центр круговой траектории и точку подвеса, при углах отклонения нити `alpha_1 = 60°` и `alpha_1 = 30°`.

Материальная точка движется по окружности с нормальным ускорением `a_n

t^4`. При этом момент силы, действующий на точку относительно центра вращения, выражается степенной функцией времени `М

t^n`. Найти значение `n`. Знак

означает пропорциональность указанных величин.

С блока радиуса `R` разматывается нить с грузом массой `m` (см. рис.). Укажите верные выражения момента импульса груза относительно оси вращения блока. На рисунке обозначены: `vectau` — радиус-вектор; `upsilon` — скорость груза; `omega` — угловая скорость блока.

Как изменится угловое ускорение вала, на котором укреплены спицы с грузами (см. рис.), если грузы переместить ближе к оси вращения? Момент сил, действующих на вал, остаётся прежним.

Однородный стержень раскручивают из состояния покоя до определенной угловой скорости. Найти отношение произведённых работ `A_а//A_б`, если ось вращения перпендикулярна стержню и проходит: а) через его конец; б) через середину.

Сравнить угловые скорости, приобретаемые телом за 5 с под действием вращающих моментов, графики которых (а и б) приведены на рисунке.

Материальная точка движется по окружности с нормальным ускорением `a_n

t^4`. При этом мощность вращающей силы выражается степенной функцией времени `N

t^n`. Найти значение п. Знак

означает пропорциональность указанных величин.

На рисунке изображено тело, имеющее ось вращения `OO_1`. Ось и векторы сил расположены в плоскости рисунка. Отличны ли от нуля относительно оси `OO_1`:

Два диска одинаковой толщины с равными массами, железный и деревянный, вращаются под действием равных по модулю сил, касательных к ободам дисков. Сравнить угловые ускорения дисков.

С наклонной плоскости одновременно начинают скатываться без проскальзывания: а) сплошной цилиндр; б) тонкостенная труба. Найти отношение скоростей `(upsilon_а//upsilon_б)` в данный момент времени.

Тело, имеющее ось вращения, приобретает за время `t` угловую скорость `omega` под действием постоянного вращающего момента `M`. Верны ли следующие выражения для работы вращающего момента при повороте тела на угол `varphi` и угола поворота?

С горки высотой `h` скатывается без проскальзывания шар. Скорость шара у основания горки вычислили по формуле `upsilon = sqrt(2gh)`. Определите погрешность результата.

Момент инерции однородного тела зависит.

Как изменяется момент сил, действующих на тело, если момент импульса тела вокруг неподвижной оси изменяется по закону

Видео:Лекция 6.5 | Нормальное и тангенциальное ускорение | Александр Чирцов | ЛекториумСкачать

Центростремительное ускорение при движении по окружности

Видео:Движение материальной точки по окружности | Физика ЕГЭ, ЦТСкачать

Равномерное движение по окружности

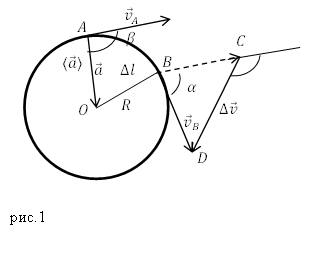
Рассмотрим равномерное движение материальной точки по окружности. При равномерном движении величина скорости постоянна ($v=const$). Однако ускорение точки при этом не равно нулю, так как скорость при движении по окружности постоянно изменяет свое направление. Вектор скорости является касательным к траектории, по которой движется точка, то есть является касательной к окружности в рассматриваемой точке

Рассмотрим точки A и B лежащие на окружности по которой движется точка. Вектор изменения скорости при перемещении частицы из А в B равен:

При бесконечно малом времени движения частицы, между точками A и B, дуга AB примерно равна длине хорды AB. Треугольники AOB и BCD подобны, поэтому получим:

где R — радиус окружности.

Величину среднего ускорения определим как:

Модуль мгновенного ускорения получаем, переходя к пределу при $Delta tto 0 $ в выражении (3):

Из формулы (4) следует, что при равномерном движении по окружности величина центростремительного ускорения не изменяется.

Вектор $overline$ имеет с $overline $угол равный$ beta $:

При $Delta tto 0 $ угол $alpha to 0.$ Получаем, что угол между вектором мгновенного ускорения и скорости при равномерном движении по окружности равен $90^circ $.

И так, материальная точка, движущаяся с постоянной скоростью по окружности, обладает ускорением, направленным к центру окружности (перпендикулярное вектору скорости), его модуль равен скорости в квадрате, деленной на радиус окружности. Такое ускорение называют центростремительным или нормальным, обозначают его обычно $_n$.

где $omega $ — угловая скорость движения материальной точки ($v=omega cdot R$).

Видео:Материальная точка равномерно движется по окружности, центр которой находится в начале O - №22689Скачать

Определение центростремительного ускорения

Центростремительное ускорение — это компонента полного ускорения материальной точки, движущейся по криволинейной траектории, характеризующая, быстроту изменения направления вектора скорости.

Центростремительное ускорение можно определить как:

Видео:Рассмотрение темы: "Тангенциальное, нормальное и полное ускорение"Скачать

Неравномерное движение материальной точки по окружности

Тангенциальное ускорение определяют как:

Впервые верные формулы для центростремительного ускорения были получены Х. Гюйгенсом.

Единицей измерения центростремительного ускорения в Международной системе единиц является метр, деленный на секунду в квадрате:

Видео:Движение тела по окружности с постоянной по модулю скоростью | Физика 9 класс #18 | ИнфоурокСкачать

Примеры задач на центростремительное ускорения

Задание. Каким будет нормальное ускорение материальной точки движущейся по окружности радиуса $R=3$м, в момент времени, равный $t=1$ c, если путь ($s$) от времени зависит как $s(t)=0,4 t^2+0,1t (м)$?

Решение. Основой для решения задачи служит определение центростремительного ускорения в виде:

Используя уравнение $sleft(tright)=0,4 t^2+0,1t и$ уравнение, связывающее мгновенное значение скорости и перемещения:

найдем величину скорости в момент времени $t=1$ с:

[vleft(tright)=frac

left(0,4 t^2+0,1tright)=0,8t+0,1to vleft(t=1 cright)=0,9 frac.]

Подставим величину скорости и радиус в (1.1) найдем величину нормального ускорения:

Ответ. $a_n=0,27frac$

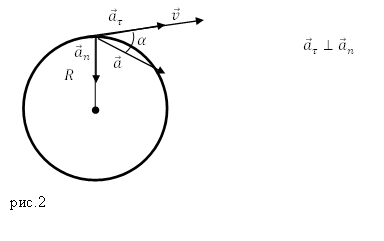
Задание. Материальная точка перемещается по окружности радиуса R. Тангенциальное ускорение этой точки равно $a_=A=const$. В какой момент времени вектор полного ускорения образует с вектором скорости угол равный $alpha $?

Решение. Сделаем рисунок.

Из рис.2 следует, что:

Величина тангенциального ускорения равна:

По условию тангенциальное ускорение постоянно и равно постоянной A. Выразим из (2.2) модуль скорости:

Центростремительное ускорение движения точки по окружности равно:

Используя (2.3) имеем:

Подставим правые части выражений (2.5) и (2.2) в формулу (2.1) [tg alpha =frac<^2>frac=frac left(2.6right).]

📹 Видео

Физика - движение по окружностиСкачать

Центростремительное ускорение. 9 класс.Скачать

Движение по окружности. Нормальное и тангенциальное ускорение | 50 уроков физики (4/50)Скачать

Точка движется по окружности радиусом R=2см. Волькенштейн 1.47Скачать

Материальная точка движется по окружности радиуса R. Что произойдет с периодом, частотой - №23387Скачать

Урок 43. Криволинейное движение. Равномерное движение по окружности. Центростремительное ускорениеСкачать

Криволинейное, равномерное движение материальной точки по окружности. 9 класс.Скачать

Физика 9 класс. Движение по окружностиСкачать

ФИЗИКА 10 класс : Механическое движение | Материальная точка, траектория, перемещение.Скачать

Криволинейное, равномерное движение материальной точки по окружности. Практическая часть. 9 класс.Скачать

ЕГЭ Задание 7. Материальная точка движется по законуСкачать

УСКОРЕНИЕ - Что такое равноускоренное движение? Как найти ускорение // Урок Физики 9 классСкачать

Кинематика Урок №8. Движение по окружности. Физика ЕГЭ 2022Скачать

Олимпиадная физика, кинематика: решение задачи на движение по окружности с ускорением | 9–11 классСкачать