Материальная точка движется по окружности кинетическая энергия

Глава 15. Теорема об изменении кинетической энергии.

15.2. Кинетическая и потенциальная энергия материальльной точки.

15.2.1. Материальная точка массой m = 1 кг движется по окружности со скоростью v = 1 м/с. Определить кинетическую энергию этой точки. (Ответ 0,5)

15.2.2. Прямолинейное движение материальной точки массой m = 4 кг задано уравнением s = 4t + 2t 2 . Определить кинетическую энергию этой точки в момент времени t = 2 с. (Ответ 288)

15.2.3. Груз массой m = 5 кг, подвешенный к вертикальной пружине, совершает свободные колебания по закону y = 0,1 sin(14t + 1,5π). Определить наибольшее значение кинетической энергии груза. (Ответ 4,9)

15.2.4. Материальная точка М массой m = 0,5 кг прикреплена к гибкой нити длиной ОМ = 2 м и совершает вместе с нитью колебания в вертикальной плоскости согласно уравнению φ = (π/6)sin 2 πt. Определить кинетическую энергию материальной точки в нижнем ее по­ложении.
(Ответ 10,8)

15.2.5. Тело 1 движется вертикально вверх со скоростью v₁ = 1 м/с. К стержню 2 длиной ОА = 0,2 м, который вращается вокруг горизонтальной оси О с постоянной угловой ско­ростью ω = 10 рад/с, прикреплен точечный груз А массой 0,1 кг. Определить кинетичес­кую энергию груза при φ = 60°. (Ответ 0,35)

15.2.6. По горизонтальной платформе на неизмен­ном расстоянии R = 1 м от оси вращения с относительной скоростью v_r = 3 м/с переме­щается материальная точка массой m = 0,2 кг. Найти ее кинетическую энергию, если платфор­ма вращается с угловой скоростью ω = 2 рад/с.
(Ответ 2,5)

15.2.7. Трубка 1 вращается равномерно с угловой скоростью ω = 2 рад/с вокруг оси АВ. Внутри трубки движется шарик 2 массой m₂ = 0,5 кг. Определить кинетическую энергию шарика в момент, когда он, находясь на расстоянии l = 0,5 м от оси, имеет относительную скорость v_r = 0,2 м/с. (Ответ 0,26)

15.2.8. Материальная точка М массой m = 0,2 кг находится в поле силы тяжести на высоте z = 10 м. Определить потенциальную энергию материальной точки, если при z = 0 потенци­альная энергия ее равна нулю. (Ответ 19,6)

15.2.9. Груз 2 совершает свободные колебания согласно закону х = 0,1 sin 10t. Жесткость пружины 1 равна 100 Н/м. Определить потенци­альную энергию груза при x = 0,05 м, если при х = 0 его потенциальная энергия равна нулю. (Ответ 0,125)

15.2.10. Груз массой 1 кг совершает свободные ко­лебания согласно закону х = 0,1 sin 10t. Коэффициент жесткости пружины с = 100 Н/м. Определить полную механическую энергию груза при х = 0,05 м, если при х = 0 потенци­альная энергия равна нулю. (Ответ 0,5)

Видео:Физика - движение по окружностиСкачать

Материальная точка движется по окружности кинетическая энергия

«Физика — 10 класс»

Почему для увеличения угловой скорости вращения фигурист вытягивается вдоль оси вращения.
Должен ли вращаться вертолёт при вращении его винта?

Заданные вопросы наводят на мысль о том, что если на тело не действуют внешние силы или действие их скомпенсировано и одна часть тела начинает вращение в одну сторону, то другая часть должна вращаться в другую сторону, подобно тому как при выбросе горючего из ракеты сама ракета движется в противоположную сторону.

Момент импульса.

Если рассмотреть вращающийся диск, то становится очевидным, что суммарный импульс диска равен нулю, так как любой частице тела соответствует частица, движущаяся с равной по модулю скоростью, но в противоположном направлении (рис. 6.9).

Но диск движется, угловая скорость вращения всех частиц одинакова. Однако ясно, что чем дальше находится частица от оси вращения, тем больше её импульс. Следовательно, для вращательного движения надо ввести ещё одну характеристику, подобную импульсу, — момент импульса.

Моментом импульса частицы, движущейся по окружности, называют произведение импульса частицы на расстояние от неё до оси вращения (рис. 6.10):

Линейная и угловая скорости связаны соотношением v = ωr, тогда

Все точки твёрдого дела движутся относительно неподвижной оси вращения с одинаковой угловой скоростью. Твёрдое тело можно представить как совокупность материальных точек.

Момент импульса твёрдого тела равен произведению момента инерции на угловую скорость вращения:

Момент импульса — векторная величина, согласно формуле (6.3) момент импульса направлен так же, как и угловая скорость.

Основное уравнение динамики вращательного движения в импульсной форме.

Угловое ускорение тела равно изменению угловой скорости, делённому на промежуток времени, в течение которого это изменение произошло: Подставим это выражение в основное уравнение динамики вращательного движения отсюда I(ω₂ — ω₁) = MΔt, или IΔω = MΔt.

Изменение момента импульса равно произведению суммарного момента сил, действующих на тело или систему, на время действия этих сил.

Закон сохранения момента импульса:

Если суммарный момент сил, действующих на тело или систему тел, имеющих неподвижную ось вращения, равен нулю, то изменение момента импульса также равно нулю, т. е. момент импульса системы остаётся постоянным.

Изменение импульса системы равно суммарному импульсу сил, действующих на систему.

Вращающийся фигурист разводит в стороны руки, тем самым увеличивает момент инерции, чтобы уменьшить угловую скорость вращения.

Закон сохранения момента импульса можно продемонстрировать с помощью следующего опыта, называемого «опыт со скамьёй Жуковского». На скамью, имеющую вертикальную ось вращения, проходящую через её центр, встаёт человек. Человек держит в руках гантели. Если скамью заставить вращаться, то человек может изменять скорость вращения, прижимая гантели к груди или опуская руки, а затем разводя их. Разводя руки, он увеличивает момент инерции, и угловая скорость вращения уменьшается (рис. 6.11, а), опуская руки, он уменьшает момент инерции, и угловая скорость вращения скамьи увеличивается (рис. 6.11, б).

Человек может также заставить вращаться скамью, если пойдёт вдоль её края. При этом скамья будет вращаться в противоположном направлении, так как суммарный момент импульса должен остаться равным нулю.

На законе сохранения момента импульса основан принцип действия приборов, называемых гироскопами. Основное свойство гироскопа — это сохранение направления оси вращения, если на эту ось не действуют внешние силы. В XIX в. гироскопы использовались мореплавателями для ориентации в море.

Кинетическая энергия вращающегося твёрдого тела.

Кинетическая энергия вращающегося твёрдого тела равна сумме кинетических энергий отдельных его частиц. Разделим тело на малые элементы, каждый из которых можно считать материальной точкой. Тогда кинетическая энергия тела равна сумме кинетических энергий материальных точек, из которых оно состоит:

Угловая скорость вращения всех точек тела одинакова, следовательно,

Величина в скобках, как мы уже знаем, это момент инерции твёрдого тела. Окончательно формула для кинетической энергии твёрдого тела, имеющего неподвижную ось вращения, имеет вид

В общем случае движения твёрдого тела, когда ось вращения свободна, его кинетическая энергия равна сумме энергий поступательного и вращательного движений. Так, кинетическая энергия колеса, масса которого сосредоточена в ободе, катящегося по дороге с постоянной скоростью, равна

В таблице сопоставлены формулы механики поступательного движения материальной точки с аналогичными формулами вращательного движения твёрдого тела.

Источник: «Физика — 10 класс», 2014, учебник Мякишев, Буховцев, Сотский

Законы сохранения в механике — Физика, учебник для 10 класса — Класс!ная физика

Видео:Теорема Кенига, кинетическая энергия тела | Олимпиадная физика, механика | 9, 10, 11 классСкачать

Формула кинетической энергии

Видео:Движение материальной точки по окружности | Физика ЕГЭ, ЦТСкачать

Определение и формула кинетической энергии

Кинетическую энергию тела определяют при помощи работы, которая совершается телом при его торможении от начальной скорости, до скорости, равной нулю.

Кинетическая энергия тела – мера механического движения тела. Она зависит от относительной скорости тел.

Встречаются следующие обозначения кинетической энергии: E_k,W_k,T.

Работу, которую производят над телом (A’) можно связать с изменением его кинетической энергии:

Видео:Теорема о кинетической энергииСкачать

Кинетическая энергия материальной точки и тела

Кинетическая энергия материальной точки равна:

где m – масса материальной точки, p – импульс материальной точки, v – скорость ее движения. Кинетическая энергия является скалярной физической величиной.

Если тело нельзя принять за материальную точку, то его кинетическая энергия рассчитывается как сумма кинетических энергий всех материальных точек, которые составляют исследуемое тело:

где dm – элементарный участок тела, который можно считать материальной точкой, dV – объем выделенного элементарного участка тела, v – скорость перемещения рассматриваемого элемента, $rho$ — плотность участка, m–масса всего рассматриваемого тела, V – объем тела.

В том случае, если тело (отличное от материальной точки) движется поступательно, то его кинетическую энергию можно рассчитать, применяя формулу (2), в которой все параметры отнесены к телу в целом.

При вращении тело вокруг неподвижной оси его кинетическую энергию можно вычислить, применяя формулу:

где J – момент инерции тела по отношению к оси вращения, ?–модуль угловой скорости вращения тела, r – расстояние от элементарного участка тела до оси вращения, L – проекция момента импульса вращающегося тела на ось во круг которой идет вращение.

Если твердое тело совершает вращение относительно неподвижной точки (например, точки O), то его кинетическую энергию находят как:

$$E_=frac <barbar>(5)$$ $bar$ – момент импульса рассматриваемого тела относительно точки О.

Видео:Движение тела по окружности с постоянной по модулю скоростью | Физика 9 класс #18 | ИнфоурокСкачать

Единицы измерения кинетической энергии

Основной единицей измерения кинетической энергии (как и любого другого вида энергии) в системе СИ служит:

в системе СГС –[E_k]= эрг.

При этом: 1 дж= 10 7 эрг.

Видео:Урок 114. Работа. Теорема о кинетической энергииСкачать

Теорема Кенига

Для самого общего случая при расчете кинетической энергии применяют теорему Кенига. В соответствии с которой, кинетическая энергия совокупности материальных точек есть сумма кинетической энергии поступательного перемещения системы со скоростью центра масс (v_c) и кинетической энергии (E’_k) системы при ее относительном движении к поступательному перемещению системы отсчета. При этом начало системы отсчета связывают с центром масс системы. Математически данную теорему можно записать как:

Так, если рассматривать твердое тело, то его кинетическую энергию можно представить как:

где J_c — момент инерции тела по отношению к оси вращения, проходящей через центр масс. В частности, при плоском движении J_c=const.В общем случае, ось (она называется мгновенной) перемещается в теле, тогда момент инерции является переменным во времени.

Видео:Урок 125. Работа, мощность и кинетическая энергия при вращательном движенииСкачать

Примеры решения задач

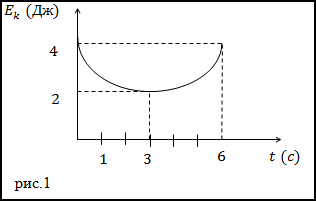
Задание. Какова работа, которая производится над телом за t=3 c (с начала отсчета времени), при силовом взаимодействии, если изменение кинетической энергии исследуемого тела задано графиком (рис.1)?

Решение. По определению изменение кинетической энергии равно работе (A’), которая производится над телом при силовом взаимодействии, то есть можно записать, что:

Исследуя график, приведенный на рис.1 мы видим, что за время t=3 c кинетическая энергия тела изменяется от 4 Дж до 2 Дж, следовательно:

💥 Видео

Потенциальная и кинетическая энергияСкачать

Консультация к устному экзамену. Механика. Часть 3: "Работа и энергия"Скачать

Д10 теорема об изменении кинетической энергииСкачать

Лекция 06 Динамика твердого телаСкачать

Консультация к устному экзамену. Механика. Часть 4: "Вращение твердых тел"Скачать

Криволинейное, равномерное движение материальной точки по окружности. 9 класс.Скачать

Материальная точка движется в поле силы тяжести по траектории, изображённой на рисунке, в - №23239Скачать

Физика - импульс и закон сохранения импульсаСкачать

Кинетическая энергия тела при плоском движенииСкачать

Материальная точка в центральном поле. Законы Кеплера. Плоское движение твердого тела. Лекция №8Скачать

Задача на теорему об изменении кинетической энергииСкачать

Якута А. А. - Механика - Динамика материальной точкиСкачать

Криволинейное, равномерное движение материальной точки по окружности. Практическая часть. 9 класс.Скачать