Ответь на вопросы. Назови элементы цилиндра (боковая поверхность, основание, ось, радиус, образующая, высота ). 2.Назови вид осевого сечения цилиндра. 3. Может ли сечение цилиндра быть: -прямоугольником (да) -квадратом (да) -трапецией?(нет). 4.Какие из данных утверждений верны: -любое сечение цилиндра плоскостью, перпендикулярной основанию есть окружность, равная окружности основания; (неверно) любое сечение цилиндра плоскостью есть окружность, равная окружности основания; (неверно) -плоскость, перпендикулярная оси цилиндра, пересекает его по кругу, равному основанию цилиндра; (верно) -сечением цилиндра могут быть круг, прямоугольник, эллипс.(верно).
Слайд 47 из презентации «Цилиндр»
Размеры: 720 х 540 пикселей, формат: .jpg. Чтобы бесплатно скачать слайд для использования на уроке, щёлкните на изображении правой кнопкой мышки и нажмите «Сохранить изображение как. ». Скачать всю презентацию «Цилиндр.ppt» можно в zip-архиве размером 6191 КБ.
Видео:Построить сечение цилиндра с плоскостью общего положения.Скачать

Цилиндр
«Цилиндром называется тело» — Задача № 2. Высота цилиндра 8 м, радиус основания 5 м. Цилиндр пересечен плоскостью так, что в сечении получился квадрат. Задача № 1. В цилиндр вписана правильная шестиугольная призма. Решение: Цилиндры. Проект «Математика в профессии «Повар, кондитер». Цилиндр, осевое сечение, которого-квадрат называется равносторонним.
«Цилиндр конус шар» — Оглавление. Найти объём и площадь поверхности шара. Определение конуса. Объёмы и поверхности тел вращения. Сечение шара плоскостью есть круг. Объема сегмента. Определение цилиндра. Завершить работу. Сечения шара. Определение шара. Тела вращения. Объём шарового сектора. Шаровой сектор . Объём шарового сегмента.
«Цилиндр» — Цилиндрическая поверхность. Объем цилиндра. Радиус цилиндра. Основания цилиндра. Цилиндр. Образующие цилиндра параллельны друг другу. Ось цилиндра.
«Понятие цилиндра» — Ножницы. Цилиндры вокруг нас. Не правда ли захватывает дух. Решение задач. Прямоугольник. Откуда и как появился цилиндр. Чудо. Сечения цилиндра. Что такое цилиндр. Счастье было потеряно навсегда. Объем цилиндра. Тело вращения. Кружочки. В честь шляпы. Добрые ножницы. Вписанный и описанный цилиндр. Два милых кружочка.
«Поверхность цилиндра» — Образующие. «Понятие цилиндра». A. Shevchenko R. Trushenkov. Осевое сечение. Стороны AB и СD — представляют собой 2 края разреза боковой поверхности цилиндра. Ось цилиндра. Основания цилиндра. Sбок = 2¶r sцил = 2¶r(r+h). «Общие формулы». Algebra & Geometria Entertainment.
«Задачи на цилиндр» — Конус. Примеры цилиндра. 1. Центры оснований цилиндра. 1. Сечением является квадрат ABCD, значит AB=AD=OO1=8дм. Площади оснований. Наклонными. Геометрическое тело, Проверь себя. Дано: цилиндр, ABCD — прямоугольник, осевое сечение. 5. Найдем площадь сечения. 4. Ось цилиндра. Какой цилиндр называется прямым?
Видео:РТ_ПБ_61.1) Построить проекции линии пересечения цилиндра плоскостью частного положения.Скачать

Любое сечение цилиндра плоскостью перпендикулярной основанию есть окружность
Если секущая плоскость пересекает ось цилиндра и не перпендикулярна ей, то в сечении может получиться эллипс (рис. 145) или его некоторая часть (рис. 146, 147). Это следует из того, что параллельной проекцией окружности на плоскость, не параллельную плоскости окружности, является эллипс. ( Вспомните : наклонив цилиндрический стеклянный сосуд с водой, вы видите на поверхности воды эллипс или его часть. )
Сечение цилиндра плоскостью, проходящей через ось, называется осевым сечением цилиндра. Так как поворот пространства вокруг прямой на угол 180 ° является осевой симметрией относительно оси вращения, то ось прямого кругового цилиндра является его осью симметрии. Значит, осевым сечением цилиндра вращения является прямоугольник, стороны которого равны диаметру основания и образующей цилиндра (рис. 148). При этом все осевые сечения цилиндра — равные между собой прямоугольники .
Цилиндр, осевое сечение которого — квадрат, называют равносторонним цилиндром (рис. 149).
Так как все образующие цилиндра равны и параллельны друг другу, то любое сечение цилиндра плоскостью, параллельной его оси, есть прямоугольник, высота которого равна образующей цилиндра (рис. 150).
б) Изображение цилиндра. Чтобы построить изображение цилиндра, достаточно построить: 1) прямоугольник AВB 1 A 1 и его ось OO 1 (рис. 151); 2) два равных эллипса, центрами которых являются точки O и O 1 и осями — отрезки АВ и A 1 В 1 . Выделив штрихами невидимые линии, получаем искомое изображение цилиндра.
в) Касательная плоскость к цилиндру.
Определение. Плоскость, проходящая через образующую цилиндра перпендикулярно плоскости осевого сечения, проведённой через эту образующую, называется касательной плоскостью к цилиндру (рис. 152).
Говорят, что плоскость α касается цилиндра ( цилиндрической поверхности ) по образующей DD 1 , каждая точка образующей DD 1 является точкой касания плоскости α и данного цилиндра.
Через любую точку боковой поверхности цилиндра проходит только одна его образующая. Через эту образующую можно провести только одно осевое сечение и только одну плоскость, перпендикулярную плоскости этого осевого сечения. Следовательно, через каждую точку боковой поверхности цилиндра можно провести лишь одну плоскость, касательную к данному цилиндру в этой точке.
17.3. Развёртка и площадь поверхности цилиндра
Следует заметить, что развёртка поверхности вращения — понятие в определённой мере интуитивное. К тому же не для каждой поверхности тела вращения можно построить её развёртку. Иными словами, не каждую поверхность можно «развернуть» на плоскости. Например, не существует развёртки сферы (см. раздел «Дифференциальная геометрия» в конце этой книги).
Развёртку цилиндра мы также введём на интуитивном уровне.
Пусть R — радиус основания, h — высота цилиндра.
Полная поверхность цилиндра состоит из его боковой поверхности и двух оснований — равных кругов. Если эту поверхность «разрезать» по образующей DD 1 (рис. 153) и по окружностям оснований, затем боковую поверхность развернуть на плоскости, то получим развёртку полной поверхности цилиндра (рис. 154), состоящую из прямоугольника и двух равных кругов, касающихся противоположных сторон этого прямоугольника (рис. 155).
Попробуйте изготовить развёртку цилиндра и склеить из неё цилиндр.
За площадь боковой поверхности цилиндра принимается площадь её развёртки , т. е. площадь боковой поверхности цилиндра равна площади прямоугольника, у которого одна сторона равна длине окружности основания цилиндра, а другая сторона — высоте цилиндра:
Таким образом, доказана следующая теорема.
Теорема 26. Площадь боковой поверхности цилиндра равна произведению длины окружности основания на высоту. ▼
Площадь круга радиуса R равна π R 2 , поэтому S осн = π R 2 . Тогда для нахождения площади полной поверхность цилиндра справедливо:
S полн = S бок + 2 S осн = 2 π Rh + 2 π R 2 = 2 π R ( R + h ) .
Следствие. Пусть цилиндр образован вращением прямоугольника ABCD вокруг его высоты AD (рис. 156) . Тогда
S бок = 2 π DC • BC . (1)
Если EF — серединный перпендикуляр к образующей BC, проведённый из точки F оси l цилиндра, то EF = CD. Учитывая, что ВС = AD, получаем: S бок = 2 π EF • AD, т. е. боковая поверхность цилиндра равна произведению высоты цилиндра на длину окружности, радиус которой равен длине серединного перпендикуляра его образующей, проведённого из точки оcu цилиндра.
Это следствие найдёт своё применение в п. 19.7.
17 . 4 . Призмы, вписанные в цилиндр и описанные около цилиндра
Нам предстоит решать задачи, в которых рассматриваются многогранники, вписанные в фигуры вращения и описанные около них.
Для правильного и наглядного изображения конфигураций из таких многогранников и фигур вращения необходимо верно изображать правильные многоугольники, вписанные в окружность (круг) или описанные около неё.
Определение. Призма называется вписанной в цилиндр, если основания призмы вписаны в основания цилиндра (рис. 157).
Цилиндр в этом случае называют описанным около призмы.
Боковые рёбра призмы соединяют соответственные вершины её оснований, вписанных в основания цилиндра. Эти вершины лежат на окружностях оснований цилиндра. Образующие цилиндра соединяют соответственные точки окружностей его оснований и параллельны боковым рёбрам призмы. Следовательно, боковые рёбра вписанной в цилиндр призмы — образующие цилиндра.
Определение. Призма называется описанной около цилиндра, если основания призмы описаны около оснований цилиндра.
Цилиндр при этом называют вписанным в призму (рис. 158).
Так как соответственные стороны оснований призмы параллельны друг другу и перпендикулярны радиусам оснований цилиндра, проведённым в точки касания, то плоскости боковых граней призмы являются касательными плоскостями к цилиндру: эти плоскости касаются поверхности цилиндра по образующим , соединяющим точки, в которых стороны оснований призмы касаются окружностей оснований цилиндра.
При изображении правильных призм, вписанных в цилиндр, следует руководствоваться алгоритмами построений изображений правильных многоугольников, вписанных в окружность.
Итак, для построения изображения правильной призмы, вписанной в цилиндр: 1) строим изображение цилиндра; 2) строим изображение правильного многоугольника, вписанного в верхнее основание цилиндра; 3) через вершины построенного вписанного многоугольника проводим образующие цилиндра; 4) в нижнем основании цилиндра последовательно соединяем концы этих образующих; 5) выделяем видимые и невидимые линии (отрезки) изображаемых фигур.
На рисунке 159 изображены вписанные в цилиндр: призма, в основании которой прямоугольный треугольник (рис. 159, а ); правильная четырёхугольная призма (рис. 159, б ); правильная треугольная призма (рис. 159, в ); правильная шестиугольная призма (рис. 159, г ).
ЗАДАЧА (3.029). Диагональ осевого сечения равностороннего цилиндра равна a 
Решени е. Рассмотрим случай а). Пусть в равносторонний цилиндр вписана правильная призма ABCA 1 B 1 C 1 (рис. 160); CDD 1 C 1 — осевое сечение; OO 1 = h — высота цилиндра; ОС = R — радиус основания цилиндра.
Так как цилиндр — равносторонний, то CDD 1 C 1 — квадрат, значит, высота цилиндра равна диаметру его основания. Тогда в квадрате СDD 1 С 1 находим CD = 
Далее, △ АВС — правильный, вписанный в основание, радиус которого R = 





S осн = 

S бок = 3 S ABB 1 A 1 = 3 AB • BB 1 = 3 • 

S полн = S бок + 2 S осн = 


Ответ: a) 

ЗАДАЧА (3.032). В равносторонний цилиндр, высота которого равна a, вписана правильная призма. Найти расстояние и угол между диагональю боковой грани призмы и осью цилиндра, если призма: а) треугольная; б) четырёхугольная; в) шестиугольная.
Решени е. Рассмотрим случай б). Пусть ABCDA 1 B 1 C 1 D 1 — вписанная в цилиндр правильная призма (рис. 161). Найдём расстояние и угол между осью OO 1 цилиндра и скрещивающейся с ней (почему?) диагональю АB 1 боковой грани ABB 1 A 1 данной призмы.
Расстояние между скрещивающимися прямыми равно расстоянию между параллельными плоскостями, проведёнными через эти прямые.
Если точка Е — середина отрезка AD, то расстояние между скрещивающимися прямыми AB 1 и OO 1 равно расстоянию между плоскостью грани ABB 1 A 1 и параллельной ей (почему?) плоскостью сечения EFF 1 E 1 . Это расстояние равно длине отрезка ОK (где точка K — середина АВ ), так как OK ⟂ ( ABB 1 ) и ( ABB 1 ) || ( EFF 1 ) .
Поскольку данный цилиндр — равносторонний, то BDD 1 B 1 — квадрат со стороной BD = ВВ 1 = a. Тогда АВ = 



Обозначим ∠ ( OO 1 ; AB 1 ) = ϕ , M = AB 1 ∩ A 1 B. Для нахождения угла ϕ проведём в грани ABB 1 A 1 прямую KK 1 || OO 1 . Тогда ϕ = ∠ ( OO 1 ; AB 1 ) = ∠ ( KK 1 ; AB 1 ) . Так как KK 1 || OO 1 , OO 1 ⟂ ( ABC ) , то MK ⟂ AB. Поэтому △ АKМ — прямоугольный. В этом треугольнике АK = 




Ответ: б) 


Действительно, S бок. пов. призм = h • P осн. призм , где Р осн. призм — периметр основания призмы, h — длина её высоты. Для правильных вписанных в цилиндр призм h — постоянная величина, равная длине высоты цилиндра, а предел последовательности периметров правильных многоугольников, вписанных в окружность (основание цилиндра), равен длине этой окружности. Таким образом, мы вновь получаем: S бок = 2 π Rh.
17.5. Объём цилиндра
Напомним принятое нами соглашение, основанное на принципе Кавальери.
«Пусть даны два тела и плоскость. Если каждая плоскость, параллельная данной плоскости и пересекающая одно из данных тел, пересекает также и другое, причём площади сечений, образованных при пересечении обоих тел, относятся как m : n, то и объёмы этих тел относятся как m : n ».
Расположим цилиндр, имеющий высоту h и радиус основания R, и прямоугольный параллелепипед с рёбрами h, R, R так, чтобы их основания находились на двух параллельных плоскостях, расстояние между которыми равно h (рис. 162). Каждая плоскость, параллельная данным плоскостям и пересекающая цилиндр, пересекает также прямоугольный параллелепипед, причём площади образованных при пересечении обоих тел сечений относятся как π • R 2 : R 2 = π : 1. Тогда и для объёмов этих тел справедливо: V цил : V парал = π : 1 или V цил : ( R 2 • h ) = π : 1, откуда
V цил = π • R 2 • h.
Если цилиндр высотой h пересечь плоскостью, параллельной его оси, то этот цилиндр разобьётся на два тела (рис. 163). Объёмы этих тел относятся как площади сегментов, образовавшихся в основании цилиндра (докажите это на основании принципа Кавальери). Следовательно, объём каждого из этих тел может быть вычислен по формуле
Любая плоскость, проведённая через середину оси цилиндра, разбивает этот цилиндр на два равновеликих тела (рис. 164), объём V каждого из которых равен половине объёма данного цилиндра, т. е. V = 
Попробуйте, исходя из этой формулы, доказать, что в таком случае объём каждой части цилиндра (см. рис. 164) может быть вычислен по формуле:
V= 
где a и b — длины отрезков, на которые образующая цилиндра делится секущей плоскостью.
Видео:усеченный цилиндр-ортогональные проекции-изометрия-разверткаСкачать

Урок геометрии в 11-м классе по теме «Понятие цилиндра. Площадь поверхности цилиндра»
Разделы: Математика
Тип урока: урок изучения нового материала.
Цели урока:
- Ввести понятия цилиндрической поверхности цилиндра и его элементов (боковая поверхность, основания, образующие, ось, высота, радиус).
- Рассмотреть сечения цилиндра плоскостью.
- Вывести формулы для вычисления площадей боковой и полной поверхностей цилиндра.
- Закрепить понятия с помощью выполнения заданий.
- Способствовать развитию у учащихся умения самостоятельно формулировать цели и задачи.
- Формировать понимание взаимосвязи между предметами математика и информатика.
- Развивать пространственное воображение.
- Воспитывать внимание, аккуратность, бережное отношение к техническим средствам.
- Способствовать осознанию ценности коллективной мыслительной деятельности.
- Формировать представление о математике, как о части общечеловеческой культуры.
Оборудование и материалы:
- ПК.
- Мультимедийный проектор.
- Интерактивная маркерная доска.
- Презентация “Цилиндр”. (Приложение 1)
- Бланки с рисунками цилиндров и самостоятельной работой. (Приложение 2)
Ход урока
Учитель: Тема нашего урока «Понятие цилиндра. Площадь поверхности цилиндра» или, кратко, “Цилиндр”. С данным геометрическим телом вы знакомы давно. Какие предметы из окружающей среды напоминают вам цилиндр?
Учитель: Используя алгоритм, по которому мы изучали многогранники в 10-м классе, подумайте и скажите, что мы можем узнать о цилиндре? (Из каких элементов состоит цилиндр; познакомиться с сечениями цилиндра; нахождение площади поверхности цилиндра).
Учитель: Сейчас вы самостоятельно поставили цель нашего урока и составили план работы. Сегодня мы будем работать по следующему плану (Слайд 2). На партах у вас раздаточный материал (лист с чертежами цилиндров). Он будет необходим при работе на уроке. Учащиеся класса будут объяснять материал используя свои презентации. Слово предоставляется Ученику №1.
Пусть L — произвольная линия, лежащая в плоскости α и m – прямая, пересекающая эту плоскость.
Цилиндрической поверхностью называется поверхность, образованная движением прямой АВ, которая непрерывно перемещается параллельно m вдоль линии L. Движущаяся прямая называется образующей, а линия L — направляющей.
Цилиндрическая поверхность называется замкнутой, если линия L- замкнутая, и незамкнутой, если линия L – незамкнутая.
Цилиндрическим телом или цилиндром называется тело, ограничение замкнутой цилиндрической поверхностью и двумя пересекающими её параллельными плоскостями:
— часть цилиндрической поверхности, ограничивающей цилиндр — боковая поверхность;
— части секущих параллельных плоскостей, выделяемые цилиндрической поверхностью — его основания;
— часть образующей цилиндрической поверхности — образующая цилиндра
— если в основании цилиндра круг — цилиндр круговой.
Другие виды цилиндров.
Учитель: Ученик № 2 расскажет нам о прямом круговом цилиндре.
Прямым круговым цилиндром называют цилиндр, у которого в основании лежат круги, а образующая перпендикулярна основаниям. В дальнейшем прямой круговой цилиндр будем называть просто “цилиндр”. Его элементы: ось, радиус, высота, образующая, основания, боковая поверхность.
Нанесите на заготовленный чертеж данные элементы и подумайте над определениями этих понятий.
Проверим, насколько верно вы дали определения.
Цилиндр можно рассматривать как тело, полученное вращением прямоугольника вокруг одной из его сторон.
Учитель: Следующий пункт плана – сечения цилиндра. На партах у вас модели цилиндров. Рассмотрите и подумайте, как можно провести сечения, и какие геометрические фигуры получатся в результате. (Прямоугольник, овал или эллипс, круг.)
Посмотрим, как они выглядят и воспроизведем на заготовках чертежей. Слово предоставляется Ученику № 3.
Слайд 10, 11, 12, 13.
Учитель: Площади боковой и полной поверхностей цилиндра. Как они вычисляются, нам расскажет Ученик № 4.
Учащийся объясняет п.54 учебника “Геометрия 10-11” (авторы: Л.С. Атанасян и др.). Полезно показать, как получается развертка на заранее приготовленной модели.
Удобно при решении задач применять следующие факты (дать понятие подобных цилиндров и отношение из полных и боковых поверхностей).
После вывода и записи формулы учащийся предлагает на 2 варианта решить задачу (Слайд 16, 17), после чего, осуществляется взаимопроверка (работа в паре).
Учитель: О цилиндрах вокруг нас нам расскажет Ученик № 5, который показывает свою презентацию.
Учитель: Переходим к проверочной работе (Слайд 39). Тексты проверочной работы лежат у каждого на парте.
Проверочная работа
Ответьте на вопросы:
- Перечислите элементы цилиндра.
- Назовите вид осевого сечения цилиндра.
- Может ли сечение цилиндра быть:
- Какие из данных утверждений верны:
— любое сечение цилиндра плоскостью, перпендикулярной основанию есть окружность, равная окружности основания;
— любое сечение цилиндра плоскостью есть окружность, равная окружности основания;
— плоскость, перпендикулярная оси цилиндра, пересекает его по кругу, равному основанию цилиндра;
— сечением цилиндра могут быть круг, прямоугольник, эллипс.
Итог
Учитель подводит итоги урока, благодарит помощников, анализирует уровень усвоения теоретического материала, задает задание на дом (Слайд 40).
📺 Видео
Задание 38. Как построить УСЕЧЕННЫЙ ЦИЛИНДР. Построение НВ фигуры сечения. Часть 1Скачать

Усеченный цилиндр: проекции сечения, изометрия, развертка поверхностиСкачать

СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать

Сечение цилиндра плоскостьюСкачать

11 класс, 27 урок, Сечения цилиндрической поверхностиСкачать

№535. Плоскость, параллельная оси цилиндра, отсекает от окружности основания дугу в 60Скачать
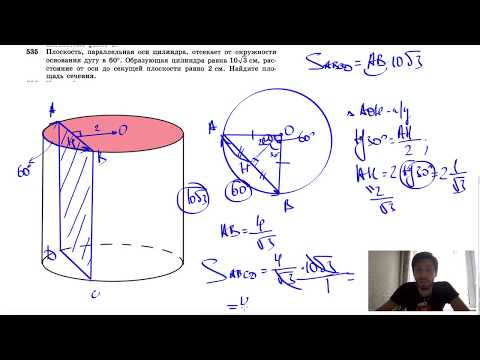
№531. Высота цилиндра равна 10 дм. Площадь сечения цилиндра плоскостью, параллельнойСкачать

[Начертательная геометрия] Сечение цилиндра плоскостью (построение в программе AutoCAD)Скачать
![[Начертательная геометрия] Сечение цилиндра плоскостью (построение в программе AutoCAD)](https://i.ytimg.com/vi/vxUMhqndPw8/0.jpg)
Компьютерная графика. 4 урок. Сечение цилиндра плоскостьюСкачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

10 класс, 14 урок, Задачи на построение сеченийСкачать

ЕГЭ №14. Задачи по стереометрии. 10-11 класс | Математика TutorOnlineСкачать

№14 из профильного ЕГЭ по математике. Как строить сечения на изи. Серия-1Скачать

Геометрия 11 класс (Урок№6 - Тела вращения. Цилиндр.)Скачать

ТЕМА 3. ПРИНЦИПЫ ПЕРЕСЕЧЕНИЯ ЦИЛИНДРА И ШАРА С ПРЯМЫМИ ПЛОСКОСТЯМИСкачать

Математика без Ху!ни. Уравнение плоскости.Скачать

Пересечение конуса и цилиндраСкачать





















