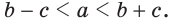Теорема 1 Любая сторона треугольника меньше суммы двух других сторон.
Доказательство. Рассмотрим произвольный треугольник ABC (Рис.1).
 |
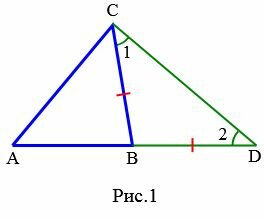Докажем, что ( small AC lt AB+BC .) На продолжении стороны AB отложим отрезок BD равный стороне BC. Полученный треугольник BCD равнобедренный. тогда ( small angle 1= angle 2.) Рассмотрим треугольник ADC. В этом треугольнике ( small angle ACD gt angle 1 ) и учитывая, что ( small angle 1= angle 2, ) получим ( small angle ACD gt angle 2. ) По теореме 1 статьи Соотношения между сторонами и углами треугольника, против большего угла треугольника лежит большая сторона. Следовательно в треугольнике ADC имеет место неравенство:
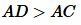 . | (1) |
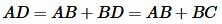 . | (2) |
Тогда из (1) и (2) получим:
  |
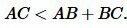Следствие 1. Для любых точек A, B, C, не расположенных на одной прямой справедливы следующие неравенства:
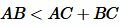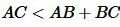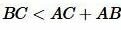 ,  ,  . | (3) |
Неравенства (3) называются неравенствами треугольника.
Видео:Неравенство треугольника ★ Любая сторона треугольника меньше суммы двух других сторонСкачать
Существующие треугольники
Определение
Существующие треугольники — это такие треугольники,
существование которых можно доказать с помощью неравенств.
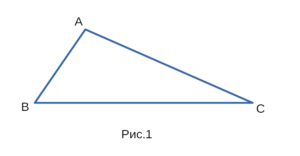
Например существование треугольника, изображенного на рисунке 1,
можно доказать с помощью неравенств: AB + BC > AC, AC + BC > AB, AB + AC > BC
Если эти три неравенства истинны значит треугольник существует,
иначе он не существует.
Также существование того или иного треугольника можно проверить с
помощью одного условия: Если большая сторона треугольника меньше
суммы двух других сторон, значит треугольник существует,
иначе он не существует.
Теорема
Для доказательства того, о чем мы говорили существует теорема под названием неравенство треугольника. Формулировка теоремы:
каждая сторона треугольника меньше суммы двух других сторон.
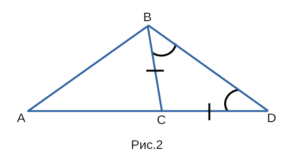
Докажем, что каждая сторона треугольника, изображенного на рисунке 2, меньше суммы двух других сторон:
Доказательство теоремы
- Проведем отрезок CD равный отрезку CB.
- △BCD — равнобедренный, значит ∠ CBD=∠CDB.
- Рассмотрим △ABD: ∠ ABD >∠ CBD, следовательно ∠ ABD >∠ CDB, то AB
Видео:Лайфхак для школьников\Теорема: каждая сторона треугольника меньше суммы двух других сторонСкачать
Неравенство треугольника — определение и вычисление с примерами решения
Содержание:
Неравенство треугольника:
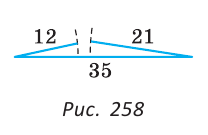
Опыт нам подсказывает, что путь из точки А в точку С по прямой АС короче, чем по ломаной ABC (рис. 255), т. е. АС 12+21 (рис. 258).
Замечание. Из неравенств треугольника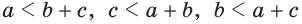 
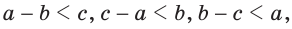
следует, что 
то есть любая сторона треугольника больше разности двух других его сторон. Так, для стороны а справедливо 
Пример:
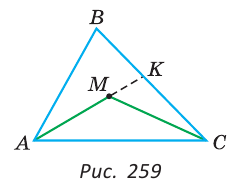
Внутри треугольника ABC взята точка М (рис. 259). Доказать, что периметр треугольника АМС меньше периметра треугольника ABC.
Решение:
Так как у треугольников ABC и АМС сторона АС — общая, то достаточно доказать, что AM + МС 
B (рис. 108, а).
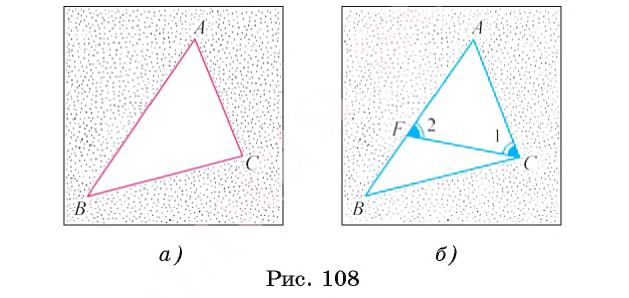
2) Отложим на стороне АВ отрезок АF, равный стороне AC (рис. 108, б).
3) Так как АF 1.
4) Угол 2 является внешним углом треугольника ВFС, следовательно, 2 > B.
5) Так как треугольник FАС является равнобедренным, то 1 = 2.
Таким образом, BСА > 1, 1 = 2 и 2 > B.
Отсюда получаем, что ВСА > B.
Теорема 2. В треугольнике против большего угла лежит большая сторона.
1) Пусть в треугольнике АBС С > B. Докажем, что АВ > АС (см. рис. 108, а). Доказательство проведем методом от противного.
2) Предположим, что это не так. Тогда: либо АВ = АС, либо АВ C.
В каждом из этих случаев получаем противоречие с условием: C > B. Таким образом, сделанное предположение неверно и, значит, АВ > АС.
Из данной теоремы следует утверждение: в прямоугольном треугольнике катет меньше гипотенузы.
Действительно, гипотенуза лежит против прямого угла, а катет — против острого. Поскольку прямой угол больше острого, то по теореме 2 получаем, что гипотенуза больше катета.
Теорема 3 (признак равнобедренного треугольника). Если два угла треугольника равны, то треугольник равнобедренный.
Пусть в треугольнике два угла равны. Тогда равны стороны, лежащие против этих углов. В самом деле, если предположить, что одна из указанных сторон больше другой, то по теореме 1 угол, лежащий против этой стороны, будет больше угла, лежащего против другой стороны, что противоречит условию равенства углов.
Значит, наше предположение неверно и в треугольнике две стороны равны, т. е. треугольник является равнобедренным.
Неравенство треугольника
Докажем, что длина каждой стороны треугольника меньше суммы длин двух других сторон.
Теорема 4. Длина каждой стороны треугольника меньше суммы длин двух других его сторон.
1) Пусть ABC — произвольный треугольник. Докажем, например, что выполняется неравенство АВ l, следовательно, верно неравенство АВF > 2.
4) Так как в треугольнике против большего угла лежит большая сторона (теорема 2), то АВ
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
🔍 Видео
Почему каждая сторона треугольника меньше суммы двух других сторон?Скачать
7 класс. Глава5. Сторона треугольника меньше суммы двух других сторонСкачать
Неравенства треугольника. 7 класс.Скачать
Найдите сторону треугольника, если другие его стороны равны 1 и 5Скачать
7 класс, 34 урок, Неравенство треугольникаСкачать
№251. Докажите, что каждая сторона треугольника больше разности двух других сторон.Скачать
Неравенство треугольника. Геометрия 7 класс. Доказательство. Задачи по рисункам.Скачать
№239. Докажите, что в треугольнике медиана не меньше высоты, проведенной из той же вершины.Скачать
Неравенства треугольникаСкачать
Каждая сторона треугольника меньше суммы...Скачать
✓ Неравенство треугольника | Ботай со мной #126 | Борис ТрушинСкачать
7 класс, 33 урок, Теорема о соотношениях между сторонами и углами треугольникаСкачать
Неравенства треугольника. Практическая часть. 7 класс.Скачать
Неравенство треугольника. Доказательство.Скачать
Неравенство треугольникаСкачать
Теорема о соотношении между сторонами треугольникаСкачать
№248. Существует ли треугольник со сторонами: а) 1 м, 2 м и 3 м; б) 1,2 дм, 1 дм и 2,4 дм?Скачать
Задача про стороны треугольника. Геометрия 7 класс.Скачать
