В окружность вписана обычная ломаная состоящая из трёх звеньев одинаковых меж собой. Расстояние меж началом и концом ломаной равно радиусу окружности. Найдите угол меж соседними звеньями ломаной. Какой ответ будет в задачке, если ломаная имеет самопересечение?
- Iskovich Svetlana
- Геометрия 2019-09-28 20:41:23 29 1
Хорда, одинаковая радиусу, образует с радиусами равносторонний треугольник, как следует стягивает дугу 60 (центральный угол равен дуге, на которую опирается).
1) Равные звенья стягивают одинаковые дуги (360-60)/3 =100
Дуга между соседними звеньями 100+60=160
Вписанный угол, опирающийся на эту дугу 160/2=80
2) Ломаная может иметь одно самопересечение (очевидно, что примыкающие звенья не пересекаются, так как теснее имеют общую точку). Тогда две дуги имеют общую часть 60 градусов.
Одинаковые звенья стягивают одинаковые дуги (360+60)/3 =140
Дуга меж примыкающими звеньями 140-60=80
Вписанный угол, опирающийся на эту дугу 80/2=40
- Ломаная
- Невырожденная ломаная
- Вырожденная ломаная
- Звенья ломаной
- Вершины ломаной
- Смежные звенья ломаной
- Смежные вершины ломаной
- Незамкнутая ломанная
- Замкнутая ломанная
- Ломаная с самопересечением
- Простая ломаная
- Длина ломаной
- Ломаная линия
- Замкнутая и незамкнутая ломаная
- Самопересекающаяся ломаная
- Длина ломаной
- 🎥 Видео
Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Ломаная
Определение 1. Ломаной (ломаной линией) ( small A_1A_2. A_A_n ) называется геометрическая фигура, которая состоит из ( small [ A_1A_2 ],) ( small [ A_2A_3 ]. ) ( small [ A_A_n ]) последовательно соединенных своими концами отрезков и никакие последовательные две отрезки( small [ A_A_ ]) и ( small [ A_A_ ]) при ( small k=1,2. n-2 ) не лежат на одной прямой.
Можно дать и другое определение ломаной:
Определение 2 . Если ( small A_1, A_2, . A_n ) различные точки, никакие проследовательные три из которых не лежат на одной прямой, то совокупность отрезков ( small [ A_1A_2 ],) ( small [ A_2A_3 ]. ) ( small [ A_A_n ]) называется ломаной или ломаной линией.
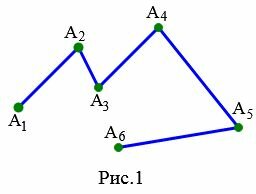
На рисунке 1 изображена ломаная состоящая из пяти отрезков ( small [ A_1A_2 ]) , ( small [ A_2A_3 ]), ( small [ A_3A_4 ]), ( small [ A_4A_5 ]), ( small [ A_5A_6 ]), которые последовательно соединены своими концами.
 |
Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Невырожденная ломаная
Ломаная, описанная в определении 1 называется невырожденной ломаной.
На рисунке 1 ломаная ( small A_1A_2A_3A_4A_5A_6 ) является невырожденной поскольку отрезки ( small [ A_1A_2 ]) и ( small [ A_2A_3 ]), ( small [ A_2A_3 ]) и ( small [ A_3A_4 ]), ( small [ A_3A_4 ]) и ( small [ A_4A_5 ]), ( small [ A_4A_5 ]) и ( small [ A_5A_6 ]) не лежат на одной прямой.
Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Вырожденная ломаная
Определение 3 . Если ( small A_1, A_2, . A_n ) различные точки, и среди них существуют проследовательные три точки, лежащие на одной прямой, то совокупность отрезков ( small [ A_1A_2 ],) ( small [ A_2A_3 ]. ) ( small [ A_A_n ]) называется вырожденной ломаной или вырожденной ломаной линией.
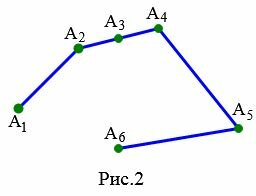 |
На рисунке 2 изображена ломаная ( small A_1A_2A_3A_4A_5A_6 ). Эта ломаная является вырожденной поскольку отрезки ( small [ A_2A_3 ]) и ( small [ A_3A_4 ]) лежат на одной прямой.
Внимание! Если явно не указыается вырожденность ломаной, то подразумевается невырожденная ломаная.
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Звенья ломаной
Звеньями называют отрезки, из которых состоит ломаная.
Ломаная ( small A_1A_2A_3A_4A_5A_6 ), изображенная на рисунке 1 состоит из звеньев ( small [ A_1A_2 ]) , ( small [ A_2A_3 ]), ( small [ A_3A_4 ]), ( small [ A_4A_5 ]), ( small [ A_5A_6 ]).
Видео:Вписанный в окружность четырёхугольник.Скачать

Вершины ломаной
Конечные точки звеньев ломаной называются вершинами.
На рисунке 1 изображена ломаная ( small A_1A_2A_3A_4A_5A_6 ), состоящая из шести вершин: ( small A_1, A_2, A_3, A_4, A_5, A_6 ).
Видео:9 класс, 24 урок, Формулы для вычисления площади правильного многоугольника, его стороныСкачать

Смежные звенья ломаной
Смежные звенья ломаной − это звенья имеющие общую вершину.
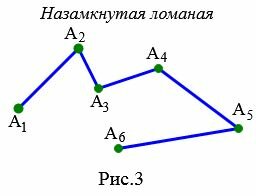
На рисунке 3 смежными звеньями ломаной ( small A_1A_2A_3A_4A_5A_6 ) являются звенья: ( small [ A_1A_2 ]) и ( small [ A_2A_3 ]), ( small [ A_2A_3 ]) и ( small [ A_3A_4 ]), ( small [ A_3A_4 ]) и ( small [ A_4A_5 ]), ( small [ A_4A_5 ]) и ( small [ A_5A_6 ]).
Видео:Геометрия 9 класс (Урок№21 - Правильный многоугольник. Описанная и вписанная окружность.)Скачать

Смежные вершины ломаной
Смежными вершинами ломаной называют вершины одного звена ломаной.
На рисунке 3 смежными вершинами ломаной ( small A_1A_2A_3A_4A_5A_6 ) являются вершины: ( small A_1) и ( small A_2), ( small A_2) и ( small A_3), ( small A_3) и ( small A_4 ), ( small A_4) и ( small A_5), ( small A_5) и ( small A_6).
Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Незамкнутая ломанная
Незамкнутым является ломаная, первая и последняя точки которой не совпадают друг с другом (Рис.3).
 |
Видео:Как решать задания на окружность ОГЭ 2021? / Разбор всех видов окружностей на ОГЭ по математикеСкачать

Замкнутая ломанная
Определение 4 . Замкнутым является ломаная ( small A_1A_2. A_A_n ), первая ( small A_1) и последняя ( small A_n ) точки которой совпадают друг с другом и отрезки ( small A_1A_2 ) и ( small A_A_n ) не лежат на одной прямой.
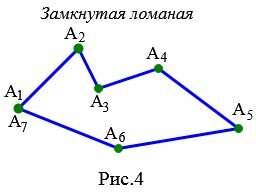 |
На рисунке 4 ломаная ( small A_1A_2A_3A_4A_5A_6A_7 ) является замкнутым, так как точки: ( small A_1) и ( small A_7) совпадают и отрезки ( small A_1A_2) и ( small A_6A_7) не лежат на одной прямой.
Видео:ОПИСАННЫЕ И ВПИСАННЫЕ ОКРУЖНОСТИ ЧЕТЫРЕХУГОЛЬНИКА . §10 геометрия 8 классСкачать

Ломаная с самопересечением
Ломаная имеет самопересечение, если хотя бы два ее звена имеют общую точку, помимо общей вершины.
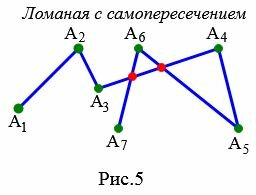 |
Ни рисунке 5 ломаная ( small A_1A_2A_3A_4A_5A_6A_7 ) имеет самопересечение, так как звенья ( small A_5A_6 ) и ( small A_6A_7 ) имеют общие точки со звеном ( small A_3A_4 ).
Видео:#32. Регион ВсОШ 2023, 9.8Скачать

Простая ломаная
Ломаная называется простым, если не имеет самопересечений. Пример простой ломаной изображен на рисунке 6.
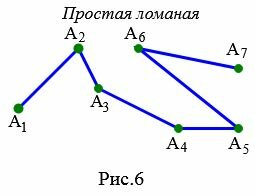 |
Видео:Правильные многоугольники. Урок 11. Геометрия 9 классСкачать

Длина ломаной
Длина ломаной равна сумме длин всех звеньев ломаной: ( small d= A_1A_2+A_2A_3+. +A_A_n, ) где ( small n ) − количество вершин ломаной.
Теорема. Длина ломаной больше расстояния между первым и последним точками.
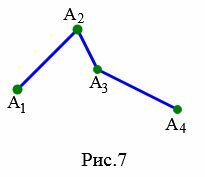 |
Доказательство. Для доказательства теоремы рассмотрим ломаную ( small A_1A_2A_3A_4 ) с тремя звеньями (Рис.7). Так как ломаная невырождена, то вершины ( small A_1, A_2, A_3 ) не лежат на одной прямой. Тогда имеет место неравенство треугольников:
| ( small A_1A_2+A_2A_3 > A_1A_3 ). | (1) |
Для точек ( small A_1, A_3, A_4 ) имеет место следующее нестрогое неравенство:
| ( small A_1A_3+A_3A_4 ≥ A_1A_4 ). | (2) |
В выражении (2) мы не применяли строгое неравенство поскольку вершины ( small A_1, A_3, A_4 ) ломаной не являются соседними вершинами и могут лежать на одной прямой.
В неравенстве (2) вместо слагаемого ( small A_1 A_3) подставим сумму ( small A_1A_2+A_2A_3 ) из (1), которая больше, чем ( small A_1 A_3). Тогда получим:
| ( small A_1A_2+A_2A_3+A_3A_4 > A_1A_4 ). |
Поседнее неравенство означает, что длина невырожденной ломаной больше расстояния между первым и последним точками.
Аналогично доказывается теорема для ломанной с любым количеством звеньев.
Видео:Пара фактов про окружность | Ботай со мной #067 | Борис Трушин |Скачать

Ломаная линия
Ломаная линия — это геометрическая фигура, состоящая из последовательно соединённых отрезков, в которой конец одного отрезка является началом следующего. При этом соседние (имеющие общую точку) отрезки не должны лежать на одной прямой.
Отрезки, из которых состоит ломаная, называются её звеньями, а концы этих отрезков — вершинами ломаной.
Построим ломаную из четырёх отрезков:
Отрезки AB, BC, CD и DE — это звенья ломаной. Точки A, B, C, D и E — вершины ломаной. Обозначение ломаной линии составляют из букв, стоящих при её вершинах, называя их по порядку. Например, говорят или пишут: ломаная ABCDE или ломаная EDCBA .
Видео:Геометрия 9 класс (Урок№26 - Построение правильных многоугольников.)Скачать

Замкнутая и незамкнутая ломаная
Незамкнутая ломаная — это ломаная линия, концы которой не совпадают друг с другом:
незамкнутая ломаная ABCD.
Замкнутая ломаная — это ломаная линия, концы которой совпадают друг с другом:
замкнутая ломаная ABC.
Видео:Многоугольники. Математика 8 класс | TutorOnlineСкачать

Самопересекающаяся ломаная
Замкнутые и незамкнутые ломаные линии могут быть самопересекающимися. Самопересекающаяся ломаная — это ломаная линия, звенья которой пересекают другу друга в одной или нескольких точках. Например:
точки F, T, K — точки самопересечения, то есть точки, в которых ломаная пересекает сама себя.
Видео:Построение пятиугольника циркулемСкачать

Длина ломаной
Длина ломаной — это сумма длин всех её звеньев. Длина замкнутой ломаной, не имеющий самопересечений, то есть длина многоугольника, называется периметром.
Пример 1. Найти длину ломаной из 3 звеньев.
Решение: Для нахождения длины ломаной, состоящей из трёх звеньев, надо сложить длины всех её звеньев. Длина ломаной ABCD будет равна:
AB + BC + CD = 4 см + 3 см + 2 см = 9 см.
Ответ: Длина ломаной ABCD равна 9 см.
Пример 2. Найти длину замкнутой ломаной.
Решение: Найдём периметр замкнутой ломаной, сложив длины всех её звеньев:
AB + BC + CD + DA =
3 см + 5 см + 4 см + 5 см = 17 см.
🎥 Видео
В поисках неравенства о ломаной | Готовимся ко ВсероссуСкачать

Разбор 16 и 23 задание ОГЭ по математике 2023 | УмскулСкачать

Волшебная школьная геометрия | Алексей Савватеев | ЛекториумСкачать

Вписанная окружность делит чевиану пополам. ЗАДАЧА - БЛЕСК!Скачать








