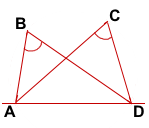
Признак принадлежности четырёх точек одной окружности
Если точки B и C лежат в одной полуплоскости относительно прямой AD, и точки B и C видны из отрезка AD под одним углом (то есть ∠ABD=∠ACD), то точки A, B, C и D лежат на одной окружности.
Дано: точки B и C лежат в одной полуплоскости относительно прямой AD,
Доказать: точки A, B, C, D лежат на одной окружности
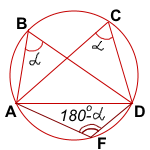
Опишем около треугольника ABD окружность.
Отметим на этой окружности произвольную точку F, лежащую относительно прямой AD в другой полуплоскости, чем точки B и C.
Четырёхугольник ABDF — вписанный в окружность. Следовательно, сумма его противолежащих углов равна 180°:
Рассмотрим четырехугольник ACDF.
Отсюда следует, что четырёхугольник ABDF — вписанный.
Поскольку около треугольника ABD можно описать только одну окружность, то точка C лежит на той же окружности, что и точки A, B и D.
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Отрезок АС виден из точек В и М под одинаковым углом…
Схема 3. У треугольников АВС и АМС сторона АС – общая, угол В равен углу М, причем точки В и М лежат по одну сторону от прямой АС. Тогда точки А, В, С, М лежат на одной окружности.
В самом деле: по теореме синусов, радиус окружности, описанной вокруг треугольника АВС, равен радиусу окружности, описанной вокруг треугольника АМС и равен А это значит, что точки А, В, М и С лежат на одной окружности.
Можно доказать и более общее утверждение: геометрическое место точек М, из которых отрезок АВ виден под данным углом, есть две дуги равных окружностей с общей хордой АВ, без точек А и В.
Задача ЕГЭ (Профильный уровень, №16)
Пусть АВ – хорда окружности с центром О, СВ – касательная к этой окружности, точки А и В лежат по разные стороны от прямой ОС. Радиус окружности ОВ равен 4, углы ОСВ и ОАВ равны.
а) Докажите, что точка О лежит на окружности Ω, описанной вокруг треугольника АВС.
б) Найдите радиус окружности Ω.
а) По условию, углы ОСВ и ОАВ равны. Отрезок ОВ виден из точек А и С под одинаковыми углами. Это значит, что четырехугольник OACB можно вписать в окружность. Тогда точка О лежит на окружности Ω, описанной вокруг треугольника АВС.
б) Мы доказали, что точка О лежит на окружности Ω, описанной вокруг треугольника АВС. Так как ВС – касательная к окружности, ВС ⊥ ОВ, ∠OBC=90°, значит, OC – диаметр. Тогда ∠OAC=90°, и треугольники ОВС и ОАС равны по гипотенузе и катету: OC – общая, OB=OA, ∠OAC=∠OВC=90°. Радиус окружности Ω равен .
Перестроим чертеж. Пусть М – точка пересечения отрезков АВ и ОС.
По условию, ОВ = 4, . Тогда . Из прямоугольного треугольника ОВМ по теореме Пифагора найдем .
Заметим, что на чертеже есть подобные прямоугольные треугольники: по двум углам.
Запишем соотношение сходственных сторон для этих треугольников:
Получим: Отсюда Это диаметр окружности Ω. Радиус в 2 раза меньше:
Видео:Доказать, что точки лежат на одной окружностиСкачать

Окружность. Относительное взаимоположение окружностей.
Если две окружности имеют только одну общую точку, то говорят, что они касаются.
Если же две окружности имеют две общие точки, то говорят, что они пересекаются.
Трех общих точек две не сливающиеся окружности иметь не могут, потому, что в противном случае через три точки можно было бы провести две различные окружности, что невозможно.
Будем называть линией центров прямую, проходящую через центры двух окружностей (например, прямую OO1).
Теорема.
Если две окружности имеют общую точку по одну сторону от линии центров, то они имеют общую точку и по другую сторону от этой линии, т.е. такие окружности пересекаются.
Пусть окружности O и O1 имеют общую точку A, лежащую вне линии центров OO1. Требуется доказать, что эти окружности имеют еще общую точку по другую сторону от прямой OO1.
Опустим из A на прямую OO1 перпендикуляр AB и продолжим его на расстояние BA1, равное AB. Докажем теперь, что точка A1 принадлежит обеим окружностям. Из построения видно, что точки O и O1 лежат на перпендикуляре, проведенном к отрезку AA1 через его середину. Из этого следует, что точка O одинаково удалена от A и A1. То же можно сказать и о точке O1. Значит обе окружности, при продолжении их, пройдут через A1.Таким образом, окружности имеют две общие точки : A (по условию) и A1 (по доказанному). Следовательно, они пересекаются.
Следствие.
Общая хорда (AA1) двух пересекающихся окружностей перпендикулярна к линии центров и делится ею пополам.
Теоремы.
1. Если две окружности имеют общую точку на линии их центров или на ее продолжении, то они касаются.
2. Обратно: если две окружности касаются, то общая их точка лежит на линии центров или на ее продолжении.
Признаки различных случаев относительного положения окружностей.
Пусть имеем две окружности с центрами O и O1, радиусами R и R1 и расстоянием между центрами d.
Эти окружности могут находиться в следующих 5-ти относительных положениях:
1. Окружности лежат одна вне другой, не касаясь. В этом случае, очевидно, d > R + R1 .
2. Окружности имеют внешнее касание. Тогда d = R + R1, так как точка касания лежит на линии центров O O1.
3. Окружности пересекаются. Тогда d R + R1, потому что в треугольнике OAO1 сторона OO1 меньше суммы, но больше разности двух других сторон.
4. Окружности имеют внутреннее касание. В этом случае в d = R — R1, потому что точка касания лежит на продолжении линии OO1.
5. Одна окружность лежит внутри другой, не касаясь. Тогда, очевидно,
d R + R1, то окружности расположены одна вне другой, не касаясь.
2. Если d = R + R1, то окружности касаются извне.
3. Если d R — R1, то окружности пересекаются.
4. Если d = R — R1, то окружности касаются изнутри.
5. Если d R Е R1. Значит, все эти случаи исключаются. Остается один возможный, именно тот, который требовалось доказать. Таким образом, перечисленные признаки различных случаев относительно положения двух окружностей не только необходимы, но и достаточны.
📽️ Видео
#207. Окружность девяти точек | лемма о трезубце | ортотреугольник | прямая ЭйлераСкачать

10 класс, 11 урок, Числовая окружностьСкачать

№8. Верно ли утверждение: а) если две точки окружности лежат в плоскостиСкачать

Четыре точки на окружности | ЕГЭ-2017. Задание 16. Математика. Профильный уровень| Борис ТрушинСкачать

Окружность, диаметр, хорда геометрия 7 классСкачать

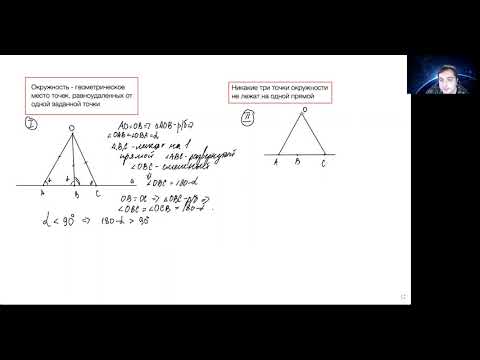
никакие три точки окружности не лежат на одной прямойСкачать
Schimbă-ți viziunea și viața ti se va schimba | Vladimir DubkovskiyСкачать

Диагностическая работа-1 в формате ОГЭ. Задача-25Скачать

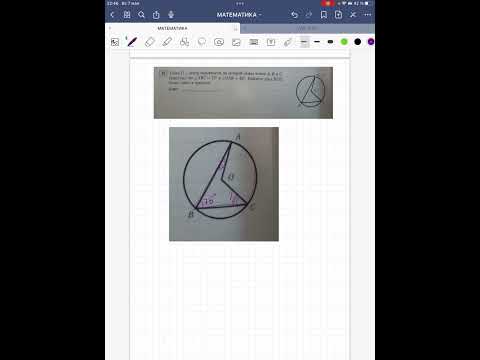
ОГЭ ЗАДАНИЕ 16 ТОЧКА О ЦЕНТР ОКРУЖНОСТИ, НА КОТОРОЙ ЛЕЖАТ ТОЧКИ А В И ССкачать
№79* Точки А, В и С лежат на одной прямой, точки М и N — середины отрезков АВ и АССкачать

Условие принадлежности четырёх точек одной окружностиСкачать

Как Эратосфен измерил диаметр Земли?Скачать

№17 Лемма о трезубце | Вписанная и вневписанная окружности | Это будет на ЕГЭ 2024 по математикеСкачать

№3. Верно ли, что: а) любые три точки лежат в одной плоскости;Скачать

Любой может закрутить глаз и другие скрытые способности телаСкачать

Математика это не ИсламСкачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

ЕГЭ Задание 16 Докажите, что три точки лежат на одной прямойСкачать