Куб пирамида треугольник шар

Геометрические объемные фигуры — это твердые тела, которые занимают ненулевой объем в евклидовом (трехмерном) пространстве. Эти фигуры изучает раздел математики, который носит название «пространственная геометрия». Знания о свойствах объемных фигур применяются в инженерии и в науках о природе. Рассмотрим в статье вопрос, геометрические объемные фигуры и их названия.

Видео:Как собрать пирамиду из неокубаСкачать

Геометрические объемные тела

Поскольку эти тела имеют конечную размерность в трех пространственных направлениях, то для их описания в геометрии используют систему из трех координатных осей. Эти оси обладают следующими свойствами:

1. Они ортогональны друг другу, то есть перпендикулярны.
2. Эти оси нормализированы, то есть базисные вектора каждой оси имеют одинаковую длину.
3. Любая из осей координат — это результат векторного произведения двух других.

Говоря о геометрических объемных фигурах и их названиях, следует отметить, что все они принадлежат к одному из 2-х больших классов:

1. Класс полиэдров. Эти фигуры, исходя из названия класса, имеют прямые ребра и плоские грани. Грань — это плоскость, которая ограничивает фигуру. Место соединения двух граней называется ребром, а точка соединения трех граней — это вершина. К полиэдрам относятся геометрическая фигура куб, тетраэдры, призмы, пирамиды. Для этих фигур справедлива теорема Эйлера, которая устанавливает связь между числом сторон (С), ребер (Р) и вершин (В) для каждого полиэдра. Математически эта теорема записывается так: С + В = Р + 2.
2. Класс круглых тел или тел вращения. Эти фигуры имеют хотя бы одну поверхность, образующую их, изогнутой формы. Например, шар, конус, цилиндр, тор.

Что касается свойств объемных фигур, то следует выделить два самых важных из них:

1. Наличие определенного объема, который фигура занимает в пространстве.
2. Наличие у каждой объемной фигуры площади поверхности.

Оба свойства для каждой фигуры описываются конкретными математическими формулами.

Рассмотрим ниже самые простые геометрические объемные фигуры и их названия: куб, пирамиду, призму, тетраэдр и шар.

Видео:Объемные Геометрические ФИГУРЫ Загадки для ДЕТЕЙСкачать

Фигура куб: описание

Под геометрической фигурой куб понимают объемное тело, которое образовано 6-тью квадратными плоскостями или поверхностями. Также эту фигуру называют правильный гексаэдр, поскольку она имеет 6 сторон, или прямоугольный параллелепипед, так как он состоит из 3-х пар параллельных сторон, которые взаимно перпендикулярны друг другу. Называют куб и прямоугольной призмой, у которой основание является квадратом, а высота равна стороне основания.

Поскольку куб является многогранником или полиэдром, то для него можно применить теорему Эйлера, чтобы определить число его ребер. Зная, что число сторон равно 6, а вершин у куба 8, число ребер равно: Р = С + В — 2 = 6 + 8 — 2 = 12.

Если обозначить буквой «a» длину стороны куба, тогда формулы для его объема и площади поверхности будут иметь вид: V = a 3 и S = 6*a 2 , соответственно.

Видео:4 класс. Математика. Геометрические тела: шар, куб, пирамида, призма, цилиндр, конусСкачать

Фигура пирамида

Пирамида — это полиэдр, который состоит из простого многогранника (основание пирамиды) и треугольников, которые соединяются с основанием и имеют одну общую вершину (вершина пирамиды). Треугольники называются боковыми гранями пирамиды.

Геометрические характеристики пирамиды зависят от того, какой многоугольник лежит в ее основании, а также от того, является ли пирамида прямой или косой. Под прямой пирамидой понимают такую пирамиду, для которой перпендикулярная основанию прямая, проведенная через вершину пирамиды, пересекает основание в ее геометрическом центре.

Одной из простых пирамид является четырехугольная прямая пирамида, в основании которой лежит квадрат со стороной «a», высота этой пирамиды «h». Для этой фигуры пирамиды объем и площадь поверхности будут равны: V = a 2 *h/3 и S = 2*a*√(h 2 +a 2 /4) + a 2 , соответственно. Применяя теорему Эйлера для нее, с учетом того, что число граней равно 5, и число вершин равно 5, получаем количество ребер: Р = 5 + 5 — 2 = 8.

Видео:Эксперимент - Обе БелыеСкачать

Фигура тетраэдр: описание

Под геометрической фигурой тетраэдр понимают объемное тело, образованное 4-мя гранями. Исходя из свойств пространства, такие грани могут представлять только треугольники. Таким образом, тетраэдр является частным случаем пирамиды, у которой в основании лежит треугольник.

Если все 4-ре треугольника, образующие грани тетраэдра, являются равносторонними и равными между собой, то такой тетраэдр называется правильным. Этот тетраэдр имеет 4 грани и 4 вершины, число ребер составляет 4 + 4 — 2 = 6. Применяя стандартные формулы из плоской геометрии для рассматриваемой фигуры, получаем: V = a 3 * √2/12 и S = √3*a 2 , где a — длина стороны равностороннего треугольника.

Интересно отметить, что в природе некоторые молекулы имеют форму правильного тетраэдра. Например, молекула метана CH₄, в которой атомы водорода расположены в вершинах тетраэдра, и соединены с атомом углерода ковалентными химическими связями. Атом углерода находится в геометрическом центре тетраэдра.

Простая в изготовлении форма фигуры тетраэдр используется также в инженерии. Например, тетраэдрическую форму используют при изготовлении якорей для кораблей. Отметим, что космический зонд НАСА, Mars Pathfinder, который совершил посадку на поверхность Марса 4 июля 1997 года, также имел форму тетраэдра.

Видео:ТЕМА 2. ПОСТРОЕНИЕ КУБА, ЦИЛИНДРА, ШАРАСкачать

Фигура призма

Эту геометрическую фигуру можно получить, если взять два многогранника, расположить их параллельно друг другу в разных плоскостях пространства, и соединить их вершины соответствующим образом между собой. В итоге получится призма, два многогранника называются ее основаниями, а поверхности, соединяющие эти многогранники, будут иметь форму параллелограммов. Призма называется прямой, если ее боковые стороны (параллелограммы) являются прямоугольниками.

Призма — это полиэдр, поэтому для нее верна теорема Эйлера. Например, если в основании призмы лежит шестиугольник, тогда, количество сторон у призмы равно 8, а количество вершин — 12. Число ребер будет равно: Р = 8 + 12 — 2 = 18. Для прямой призмы высотой h, в основании которой лежит правильный шестиугольник со стороной a, объем равен: V = a 2 *h*√3/4, площадь поверхности равна: S = 3*a*(a*√3 + 2*h).

Видео:Натюрморт из геометрических предметовСкачать

Фигура шар

Говоря о простых геометрических объемных фигурах и их названиях, следует упомянуть шар. Под объемным телом под названием шар понимают тело, которое ограничено сферой. В свою очередь, сфера — это совокупность точек пространства, равноудаленных от одной точки, которая называется центром сферы.

Поскольку шар относится к классу круглых тел, то для него не существует понятия о сторонах, ребрах и вершинах. Площадь поверхности сферы, ограничивающей шар, находится по формуле: S = 4*pi*r 2 , а объем шара можно вычислить по формуле: V = 4*pi*r 3 /3, где pi — число пи (3,14), r — радиус сферы (шара).

Видео:Как нарисовать ШАР (сфера). Построение , штриховка.Скачать

Геометрические объемные фигуры и их названия: шар, куб, пирамида, призма, тетраэдр

Видео:Тема 71. Геометрические тела: шар, куб, пирамида, призма, цилиндр, конусСкачать

Геометрические объемные тела

Поскольку эти тела имеют конечную размерность в трех пространственных направлениях, то для их описания в геометрии используют систему из трех координатных осей. Эти оси обладают следующими свойствами:

1. Они ортогональны друг другу, то есть перпендикулярны.
2. Эти оси нормализированы, то есть базисные вектора каждой оси имеют одинаковую длину.
3. Любая из осей координат — это результат векторного произведения двух других.

Говоря о геометрических объемных фигурах и их названиях, следует отметить, что все они принадлежат к одному из 2-х больших классов:

1. Класс полиэдров. Эти фигуры, исходя из названия класса, имеют прямые ребра и плоские грани. Грань — это плоскость, которая ограничивает фигуру. Место соединения двух граней называется ребром, а точка соединения трех граней — это вершина. К полиэдрам относятся геометрическая фигура куб, тетраэдры, призмы, пирамиды. Для этих фигур справедлива теорема Эйлера, которая устанавливает связь между числом сторон (С), ребер (Р) и вершин (В) для каждого полиэдра. Математически эта теорема записывается так: С + В = Р + 2.
2. Класс круглых тел или тел вращения. Эти фигуры имеют хотя бы одну поверхность, образующую их, изогнутой формы. Например, шар, конус, цилиндр, тор.

Что касается свойств объемных фигур, то следует выделить два самых важных из них:

1. Наличие определенного объема, который фигура занимает в пространстве.
2. Наличие у каждой объемной фигуры площади поверхности.

Оба свойства для каждой фигуры описываются конкретными математическими формулами.

Рассмотрим ниже самые простые геометрические объемные фигуры и их названия: куб, пирамиду, призму, тетраэдр и шар.

Видео:Урок 3 конус, бублик, сфера, пирамида и другие геометрические фигуры в SketchUp.Скачать

Фигура куб: описание

Под геометрической фигурой куб понимают объемное тело, которое образовано 6-тью квадратными плоскостями или поверхностями. Также эту фигуру называют правильный гексаэдр, поскольку она имеет 6 сторон, или прямоугольный параллелепипед, так как он состоит из 3-х пар параллельных сторон, которые взаимно перпендикулярны друг другу. Называют куб и прямоугольной призмой, у которой основание является квадратом, а высота равна стороне основания.

Поскольку куб является многогранником или полиэдром, то для него можно применить теорему Эйлера, чтобы определить число его ребер. Зная, что число сторон равно 6, а вершин у куба 8, число ребер равно: Р = С + В — 2 = 6 + 8 — 2 = 12.

Если обозначить буквой «a» длину стороны куба, тогда формулы для его объема и площади поверхности будут иметь вид: V = a3 и S = 6*a2, соответственно.

Видео:Миникурс по геометрии. Куб, призма, цилиндр и конусСкачать

Как изготовить карточки Домана самостоятельно:

Распечатайте карточки на плотной бумаге или картоне по 2, 4 или 6 штук на 1 листе. Для проведения занятий по методике Домана карточки готовы, Вы их можете показывать малышу и называть название картинки.

Успехов и новых открытий Вашему малышу!

Развивающее видео для детей (малышей и дошкольников) выполненное по методике Домана «Вундеркинд с пеленок» — развивающие карточки, развивающие картинки на различные темы из части 1, части 2 методики Домана, которое можно смотреть бесплатно здесь или на нашем Канале Раннее развитие детей на youtube

Развивающие карточки по методике Глена Домана с картинками объемных геометрических фигур для детей

Развивающие карточки по методике Глена Домана с картинками объемных геометрических фигур для детей

Развивающие карточки по методике Глена Домана с картинками объемных геометрических фигур для детей

Развивающие карточки по методике Глена Домана с картинками объемных геометрических фигур для детей

Развивающие карточки по методике Глена Домана с картинками объемных геометрических фигур для детей

Развивающие карточки по методике Глена Домана с картинками объемных геометрических фигур для детей

Развивающие карточки по методике Глена Домана с картинками объемных геометрических фигур для детей

Развивающие карточки по методике Глена Домана с картинками объемных геометрических фигур для детей

Развивающие карточки по методике Глена Домана с картинками объемных геометрических фигур для детей

Развивающие карточки по методике Глена Домана с картинками объемных геометрических фигур для детей

Развивающие карточки по методике Глена Домана с картинками объемных геометрических фигур для детей

Развивающие карточки по методике Глена Домана с картинками объемных геометрических фигур для детей

Развивающие карточки по методике Глена Домана с картинками объемных геометрических фигур для детей

Развивающие карточки по методике Глена Домана с картинками объемных геометрических фигур для детей, карточки домана бесплатно

Развивающие карточки по методике Глена Домана с картинками объемных геометрических фигур для детей, карточки домана бесплатно

Развивающие карточки по методике Глена Домана с картинками объемных геометрических фигур для детей, карточки домана бесплатно

Развивающие карточки по методике Глена Домана с картинками объемных геометрических фигур для детей, карточки домана бесплатно

Видео:Академический рисунок кубаСкачать

Фигура пирамида

Пирамида — это полиэдр, который состоит из простого многогранника (основание пирамиды) и треугольников, которые соединяются с основанием и имеют одну общую вершину (вершина пирамиды). Треугольники называются боковыми гранями пирамиды.

Геометрические характеристики пирамиды зависят от того, какой многоугольник лежит в ее основании, а также от того, является ли пирамида прямой или косой. Под прямой пирамидой понимают такую пирамиду, для которой перпендикулярная основанию прямая, проведенная через вершину пирамиды, пересекает основание в ее геометрическом центре.

Одной из простых пирамид является четырехугольная прямая пирамида, в основании которой лежит квадрат со стороной «a», высота этой пирамиды «h». Для этой фигуры пирамиды объем и площадь поверхности будут равны: V = a2*h/3 и S = 2*a*√(h2+a2/4) + a2, соответственно. Применяя теорему Эйлера для нее, с учетом того, что число граней равно 5, и число вершин равно 5, получаем количество ребер: Р = 5 + 5 — 2 = 8.

Видео:Геометрические тела.Скачать

Презентация к уроку «Объемные геометрические фигуры» презентация к уроку по математике на тему

Цилиндр Конус – геометрическая фигура, полученное объединением всех лучей, исходящих из одной точки и проходящих через плоскую поверхность. Конус в переводе с греческого « konos » означает «сосновая шишка». Конус Призма Объёмные геометрические фигуры ● Шар. Сфера. ● Цилиндр ● Параллелепипед ● Куб ● Конус ● Пирамида ● Призма Сказка про параллелограмм и его дружную семейку Жил был параллелограмм со своей женой трапецией . У параллелограмма были такие свойства: противоположные стороны и углы равны; диагонали пересекаются и точкой пересечения делятся пополам. А у его жены трапеции только то, что две противоположные стороны параллельны, а две другие нет. И вот у них родился долгожданный сын прямоугольник . По наследству ему передавались те же свойства, что у папы и добавилось еще одно свойство: диагонали равны. Так он рос год за годом и, к удивлению родителей, все его стороны и он стал четырехугольником, у которого все углы и стороны равны. И стали звать его квадратом . При этом он приобрел еще два свойства: диагонали взаимно перпендикулярны и являются биссектрисами его углов. Так проходили годы, и когда квадрат стал юношей, он снова стал меняться, вытянулся… его углы изменились, и родители назвали его ромбом . Свойства у него остались те же кроме одного, что углы прямые. Цилиндр Вот что однажды написали в газете (от 26 января 1797 года) про изобретателя цилиндра: «Джон Гетерингтон гулял вчера по тротуару набережной, имея на голове громадную трубу, сделанную из шелка, отличавшуюся странным блеском. Действие ее на прохожих было ужасным. Многие женщины при виде этого странного предмета лишались чувств, дети кричали, а один молодой человек, возвращающийся как раз от мыловара, у которого он сделал несколько покупок, был сбит в давке с ног и сломал руку. По этому случаю господину Гетерингтону пришлось вчера отвечать перед лорд-мэром, куда он был приведен отрядом вооруженной полиции. Арестованный объявил, что он считает себя вправе показывать своим лондонским покупателям новейшее свое изобретение, с каковым мнением лорд-мэр, однако, не согласился, присудив изобретателя блестящей трубы к уплате штрафа в 500 фунтов стерлингов». Куб Призма — многогранник, который состоит из двух плоских равных многоугольников с соответственно параллельными сторонами, и из отрезков, соединяющих соответствующие точки этих многоугольников. Призма В составлении презентации использовались интернет ресурсы Объёмные геометрические фигуры Презентацию подготовила учитель ГБОУ СОШ № 242 Гронская Наталья Николаевна Пирамида Сказка про параллелограмм

и его дружную семейку Жил был параллелограмм со своей женой трапецией . У параллелограмма были такие свойства: противоположные стороны и углы равны; диагонали пересекаются и точкой пересечения делятся пополам. А у его жены трапеции только то, что две противоположные стороны параллельны, а две другие нет. И вот у них родился долгожданный сын прямоугольник . По наследству ему передавались те же свойства, что у папы и добавилось еще одно свойство: диагонали равны. Так он рос год за годом и, к удивлению родителей, все его стороны и он стал четырехугольником, у которого все углы и стороны равны. И стали звать его квадратом . При этом он приобрел еще два свойства: диагонали взаимно перпендикулярны и являются биссектрисами его углов. Так проходили годы, и когда квадрат стал юношей, он снова стал меняться, вытянулся… его углы изменились, и родители назвали его ромбом . Свойства у него остались те же кроме одного, что углы прямые. Назови имена членов дружной семейки Цилиндр – в элементарной геометрии, геометрическое тело, образованное вращением прямоугольника около одной стороны. Цилиндр Куб – это один из пяти правильных многогранников Правильный прямоугольный параллелепипед имеет 6 граней, 12 ребер, 8 вершин. Куб Спасибо за внимание! Шар; Сфера Пирамида – многогранник, основание которого многоугольник, а остальные грани – треугольники, имеющие общую вершину. Пирамида Геометрия вокруг нас, нужно только присмотреться! Параллелепипед Назови плоские геометрические фигуры Шар — геометрическое тело ; совокупность всех точек пространства, находящихся от центра на расстоянии , не больше заданного. Это расстояние

называется радиусом шара. Шар образуется вращением полукруга около его неподвижного диаметра . Этот диаметр называется осью шара, а оба конца указанного диаметра — полюсами шара. Поверхность шара называется сферой: замкнутый шар включает эту сферу, открытый шар — исключает. Шар; Сфера Параллелепипед – это призма, основанием которой служит параллелограмм, или многогранник, у которого шесть граней и каждая из них — параллелограмм. Параллелепипед

Конус Взгляд на геометрию со стороны…. Биолог: «…Квадраты — вид — фигура рода Прямоугольники, семейства Параллелограммы, отряда Четырёхугольники, класса Многоугольники, типа Плоские фигуры, царства Фигуры. Некоторые биологи также относят квадрат к роду Ромбы, что, конечно же, ошибочно. Любой школьник знает, что стороны ромба, в отличие от квадрата, проводятся не по горизонтали и по вертикали, а по диагонали. В зависимости от формата окружающей среды размер фигуры может варьировать от нескольких миллиметров до нескольких миль и даже больше, если начертить её на карте мира»

Видео:Объёмные геометрические фигуры. Куб. Цилиндр. Конус. Шар // Математика 1 классСкачать

Фигура тетраэдр: описание

Под геометрической фигурой тетраэдр понимают объемное тело, образованное 4-мя гранями. Исходя из свойств пространства, такие грани могут представлять только треугольники. Таким образом, тетраэдр является частным случаем пирамиды, у которой в основании лежит треугольник.

Если все 4-ре треугольника, образующие грани тетраэдра, являются равносторонними и равными между собой, то такой тетраэдр называется правильным. Этот тетраэдр имеет 4 грани и 4 вершины, число ребер составляет 4 + 4 — 2 = 6. Применяя стандартные формулы из плоской геометрии для рассматриваемой фигуры, получаем: V = a3*√2/12 и S = √3*a2, где a — длина стороны равностороннего треугольника.

Интересно отметить, что в природе некоторые молекулы имеют форму правильного тетраэдра. Например, молекула метана CH4, в которой атомы водорода расположены в вершинах тетраэдра, и соединены с атомом углерода ковалентными химическими связями. Атом углерода находится в геометрическом центре тетраэдра.

Простая в изготовлении форма фигуры тетраэдр используется также в инженерии. Например, тетраэдрическую форму используют при изготовлении якорей для кораблей. Отметим, что космический зонд НАСА, Mars Pathfinder, который совершил посадку на поверхность Марса 4 июля 1997 года, также имел форму тетраэдра.

Видео:Как нарисовать пирамиду?Скачать

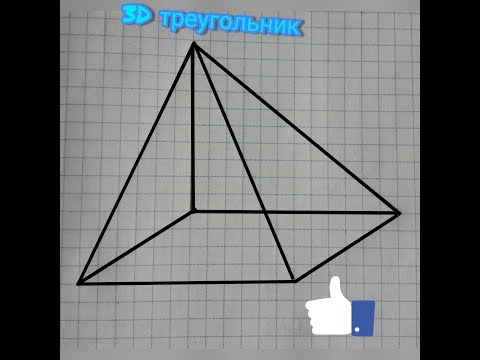
Изображения объемных правильных многогранников

1. Тетраэдр — правильный многогранник (четырёхгранный), имеющий 4 грани, они, в свою очередь, оказываются правильными треугольниками. У тетраэдра 4 вершины, к каждой из них сходится 3 ребра. Общее количество ребер у тетраэдра 6.
   Правильный тетраэдр
2. Гексаэдр(куб) — правильный многогранник (шестигранный), каждая грань которого представляет собой квадрат.
   Изображение куба
3. Октаэдр — многогранник с восемью гранями; грани правильного октаэдра — восемь равносторонних треугольников.
   Изображение октаэдра

Видео:Как легко собрать шар из НЕОКУБА!Скачать

Фигура призма

Эту геометрическую фигуру можно получить, если взять два многогранника, расположить их параллельно друг другу в разных плоскостях пространства, и соединить их вершины соответствующим образом между собой. В итоге получится призма, два многогранника называются ее основаниями, а поверхности, соединяющие эти многогранники, будут иметь форму параллелограммов. Призма называется прямой, если ее боковые стороны (параллелограммы) являются прямоугольниками.

Призма — это полиэдр, поэтому для нее верна теорема Эйлера. Например, если в основании призмы лежит шестиугольник, тогда, количество сторон у призмы равно 8, а количество вершин — 12. Число ребер будет равно: Р = 8 + 12 — 2 = 18. Для прямой призмы высотой h, в основании которой лежит правильный шестиугольник со стороной a, объем равен: V = a2*h*√3/4, площадь поверхности равна: S = 3*a*(a*√3 + 2*h).

Видео:4D фигурыСкачать

Фигура шар

Говоря о простых геометрических объемных фигурах и их названиях, следует упомянуть шар. Под объемным телом под названием шар понимают тело, которое ограничено сферой. В свою очередь, сфера — это совокупность точек пространства, равноудаленных от одной точки, которая называется центром сферы.

Поскольку шар относится к классу круглых тел, то для него не существует понятия о сторонах, ребрах и вершинах. Площадь поверхности сферы, ограничивающей шар, находится по формуле: S = 4*pi*r2, а объем шара можно вычислить по формуле: V = 4*pi*r3/3, где pi — число пи (3,14), r — радиус сферы (шара).

Видео:Как сделать ЧЕТЫРЕХУГОЛЬНУЮ ПИРАМИДУ из бумаги? ||| Геометрические фигуры своими рукамиСкачать

Конспект: «Распознавание и называние геометрических тел: куб, шар, пирамида, цилиндр»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

МАТЕМАТИКА , 4 КЛАСС

ТЕМА. РАСПОЗНАВАНИЕ И НАЗЫВАНИЕ ГЕОМЕТРИЧЕСКИХ ТЕЛ: КУБ, ШАР, ПИРАМИДА, ЦИЛИНДР.

ЦЕЛИ УРОКА: формировать умение распознавать и называть геометрические тела: куб, шар, пирамида, цилиндр, изготавливать модели геометрических тел из бумаги с использованием развёрток, моделировать разнообразные ситуации расположения объектов в пространстве и на плоскости, соотносить реальные объекты с моделями многогранников и шара; развивать внимание, логическое мышление, умение исследовать ; прививать интерес к изучению математики.

I .ОРГАНИЗАЦИЯ КЛАССА

Чтоб работа закипела,

Ты берись за дело смело.

И решай всё так как нужно:

Быстро, правильно и дружно!

II .АКТУАЛИЗАЦИЯ ОПОРНЫХ ЗНАНИЙ И УМЕНИЙ УЧАЩИХСЯ

Задание: решить примеры и их результаты расставить в порядке возрастания.

Распределение фигур по группам ( дети называют фигуры и распределяют их на плоские и объёмные)

— На сколько групп можно разделить эти фигуры?

Сравнение и распределение плоских и объёмных фигур. Работа в группах .

-Какие бывают фигуры?

— Посмотрите, что перед вами лежит?

— Разделите их на 2 группы.

— Проверяем, как вы это сделали.

— Почему эти фигуры вы объединили в 1 группу, а эти во 2 группу?

5. Определение целей урока

-А как вы думаете, о чем будем говорить на уроке?

— Как вы думаете, вы о них все знаете?

-Значит, какая наша цель?

III . СООБЩЕНИЕ ТЕМЫ И ЦЕЛЕЙ УРОКА

IV. ОЗНАКОМЛЕНИЕ С НОВЫМ МАТЕРИАЛОМ

(У учащихся на парте лежит листок, на котором записаны примеры. Решив их, они могут расшифровать слово-название фигуры , с которой будут работать. )

Карточки для групп

— Какое число лишнее? Почему?

2. Конструирование объёмной фигуры по данной развёртке.

Работа в группах : 1 группа склеивает куб,

группа – лепит из пластилина шар,

3 группа – пирамиду,

4 группа – цилиндр.

3.Гимнастика для глаз.

Рисуй глазами треугольник.

Теперь его переверни вершиной вниз.

И вновь глазами ты по периметру веди.

Рисуй восьмерку вертикально.

Ты головою не крути,

А лишь глазами осторожно ты вдоль по линиям води.

И на бочок ее клади.

Теперь следи горизонтально,

И в центре ты остановись.

Зажмурься крепко, не ленись.

Глаза открываем мы, наконец.

Зарядка окончилась. Ты молодец!

Учитель на одной из фигур объясняет , где у фигуры грани, ребра, вершины, основание.

(Каждая группа исследует заданную фигуру, заполняя определенный столбец таблицы. В ходе защиты своих работ, заполняется вся таблица и дети, таким образом ознакамливаются со всеми фигурами ).

Способность кататься (в каких направлениях)

(во всех направ-лениях)

На какие предметы похожа фигура

кубики для детей…

Пакетик чая, пирамида Хеопса, крыши домов…

Шляпа фокусника,труба, коробка для печенья…

Каждой из команд даны приложения подсказки, которыми они могут воспользоваться при защите работ.

Подсказка для команды «КУБ»

Ящик — КУБ,
в нём шесть сторон,
все стороны — квадраты.
А что лежит в посылке?
Там стружки и опилки,
конфеты и баранки,
ещё с вареньем банки.

Слово «куб» произошло от греч. κύβος «игральная кость; кубическое тело»,

Подсказка для команды «ШАР»
Удар! Удар! Ещё удар!
Летит в ворота мячик —
ШАР!
А это — шар арбузный,
зелёный, круглый, вкусный.
Вглядитесь лучше –
шар каков !
Он сделан из одних кругов.
Разрежьте на круги арбуз
И их попробуйте на вкус.

Слово «шар» произошло от греческого слова оφατρα , что означает «мяч».

Подсказка для команды «ПИРАМИДА»

Я видел картину.
На этой картине стоит
ПИРАМИДА в песчаной пустыне.
Всё в пирамиде необычайно.
Какая-то есть в ней
загадка и тайна.
А Спасская башня
на площади Красной
и детям, и взрослым
знакома прекрасно.
Посмотришь на башню —
обычная с виду.
А что на вершине у ней?
— Пирамида.

Слово «пирамида» произошло от греческого слова «пюрамис», которым греки называли египетские пирамиды. Средневековые ученые считали, что слово пирамида происходит от греческого слова огонь, так как пламя иногда напоминает по форме пирамиду.

— Одним из интересных фактов является то, что продукты, находящиеся в упаковке в виде пирамиды, лучше и дольше сохраняются.
— Знаменитую пирамиду Хеопса строили 4000 человек в течение 30 лет.

Подсказка для команды «ЦИЛИНДР»

Цилиндр, что такое? — спросил я у папы.
Отец рассмеялся : — Цилиндр, это шляпа.
Чтобы иметь представление верное,
Цилиндр, скажем так, это банка консервная.
Труба парохода- цилиндр,
Труба на нашей крыше — тоже,
Все трубы на цилиндр похожи.
А я привёл пример такой —
Калейдоскоп любимый мой,
Глаз от него не оторвёшь,
И тоже на цилиндр похож.

Очень давно, когда не было ещё машин и тракторов, и никакой другой техники, люди, чтобы перетащить тяжёлый груз с одного места на другое, использовали катки из дерева. Они подыскивали прямое дерево и отрезали от него кусок. Этот кусок и служил катком.

Слово «цилиндр» произошло от греческого слова ξνλινδροσ . Означало оно «каток», «валик».

6. Защита исследовательской работы.

7.Выводы – определения. Составление словаря.

КУБ – объёмная геометрическая фигура, каждая грань которой представляет собой квадрат. Все ребра куба равны.

ПИРАМИДА – объёмная геометрическая фигура, основание которой – многоугольник, а остальные грани – треугольники, имеющие общую вершину.

ЦИЛИНДР — объёмная геометрическая фигура, состоящая из боковой поверхности и двух оснований в виде кругов.

ШАР — объёмная геометрическая фигура, у которого не существует основания и вершин, все точки равноудалены от центра.

Представьте, что вы в конусе. Тянемся к его вершине.

А теперь мы в цилиндре. Постучите ногами по его основанию.

V .ЗАКРЕПЛЕНИЕ И ОСМЫСЛЕНИЕ ИЗУЧЕННОГО МАТЕРИАЛА.

1. Выполнение упражнений данных в учебнике.

— с.110 задание №2- начертить развертку куба и нарисовать в ней заданные предметы так, чтобы они располагались напротив друг друга;

— с. 113 задание № 2 (1) — сравнить квадрат и круг; куб и шар;

квадрат и куб; круг и шар.

(Задание распределяется и выполняется по группам)

— с. 113 задание № 2 (2) – разбить фигуры на две группы разными способами

(по цвету, форме и т.д.)

Работа с таблицей.
Число вершин пирамиды на _________ больше числа вершин в ее основании.

Ребер боковых граней _____________ , сколько их в основании.

Число боковых граней _______________ числу сторон основания.

(После выполнения задания проверить выводы. Листочки собрать.)

Ответы:

Число вершин пирамиды на единицу больше числа вершин в ее основании.

Ребер боковых граней столько же , сколько их в основании.

Число боковых граней равно числу сторон основания.

3.Выполнение логических заданий

Задание. Найди лишнюю фигуру.

Задание. К какому кубику подходит данная развертка?

VII . РЕФЛЕКСИЯ. ПОДВЕДЕНИЕ ИТОГОВ

— мне на уроке было все понятно

— на уроке мне было интересно

— я почувствовал, что могу выполнить домашнее задание

— мне сегодня было трудно и не все понятно

📺 Видео

Пирамида из НЕОКУБА | ФИГУРЫ из неокубаСкачать

Собираю огромную Пирамиду из 1000 магнитов и шариков! 🔺 Alex BoykoСкачать

оригами пирамида как сделать пирамиду из бумаги схема пирамида хеопса How to make Paper PyramidСкачать