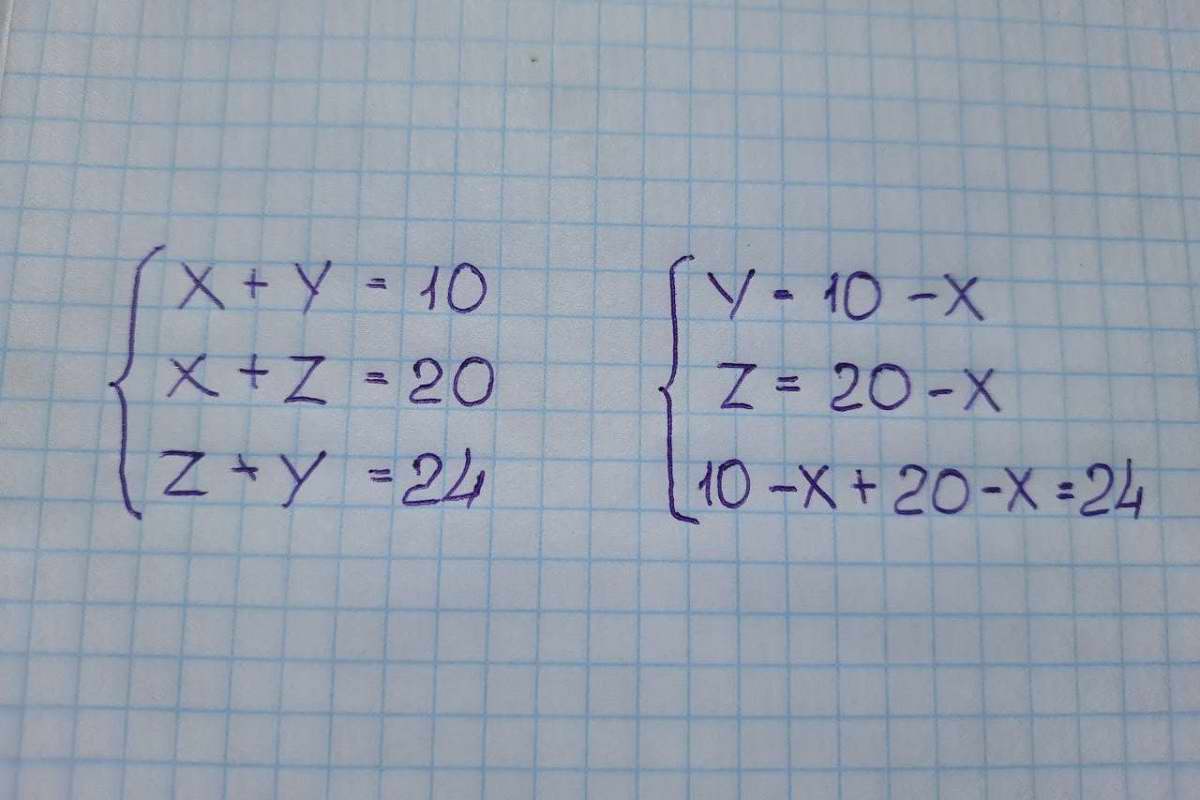Круг плюс треугольник равно

Сумму из трех чисел ( круг, квадрат, треугольник — схема примера) можно записать шестью разными способами. Нарисуй в тетради все возможные суммы.

1).круг+квадрат+треугольник

2). круг+?+?

3). квадрат+?+?

4). ?+?+?

5). треугольник+?+?

6). ?+?+?

*Как ты думаешь,какие из этих сумм имеют одинаковые значения?

*Выбери любые три числа и проверь свое предположение: подставь числа в схемы и вычисли суммы

Видео:Задача, которую боятсяСкачать

Почему нынче в школе первый класс вроде института

Метки

Эти сложные математические задачи мы взяли из обычных учебников для начальной школы. Родители возмущены и недоумевают: «Что за безобразие, как их вообще решить без иксов и систем уравнений?»

Похоже, Алла Борисовна знала об этой проблеме еще в 1980 году. Нынче в школе первый класс — действительно что-то вроде института. Но, в отличие от эмоционального кандидата наук из «Песенки первоклассника», мы не станем над задачами плакать. Попробуем найти для них простые решения.

Видео:Квадратура круга: математически невозможная задача, оказавшаяся решаемойСкачать

Сложные математические задачи

Круги, треугольники и квадраты

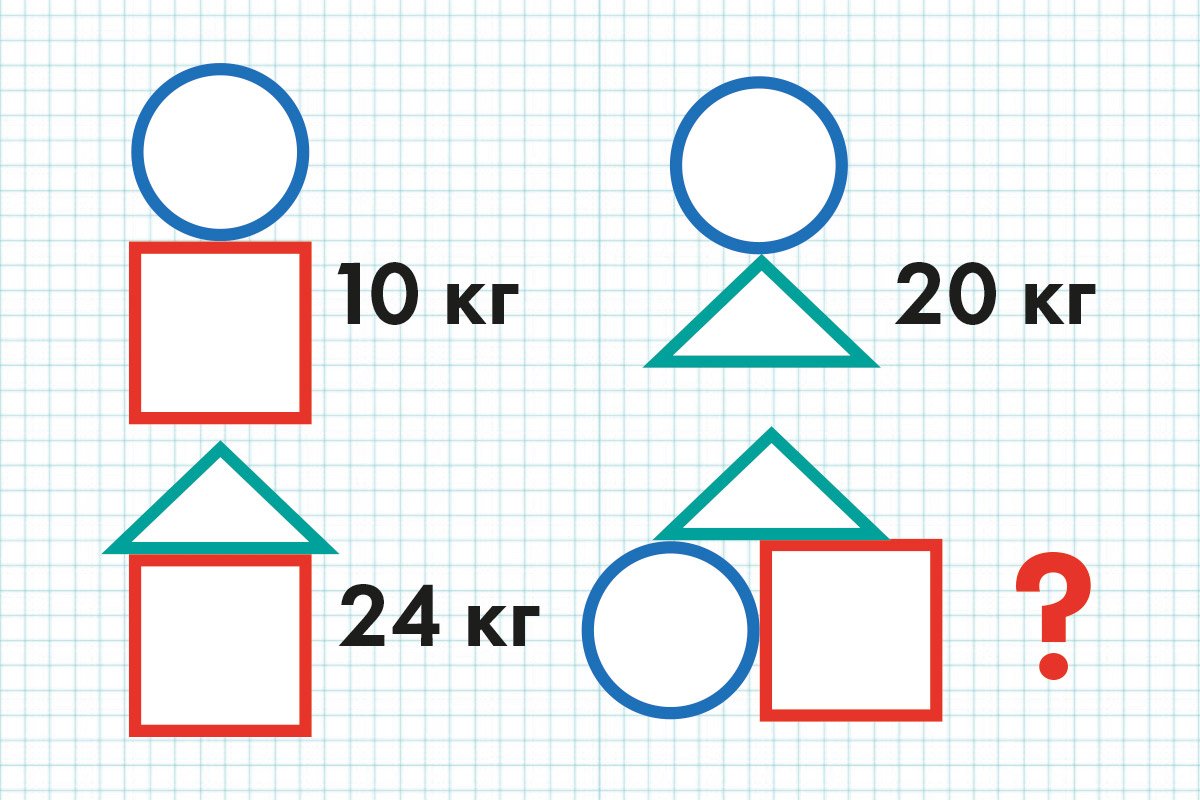
Задачка для первого класса со звездочкой (повышенной сложности). Требуется найти, чему равна сумма круга, треугольника и квадрата.

У взрослого человека, знакомого с алгеброй, первое побуждение — составить систему из трех уравнений. Если круг — это х, квадрат — y, а треугольник — z, получаем:

Отсюда 30 — 2х = 24; 2х = 6; х = 3. Круг (х) равен 3, значит квадрат (у) равен 7, а треугольник (z) — 17. Сумма круга, треугольника и квадрата дает нам 27 кг.

Но системы уравнений начинают изучать только на уроках алгебры в 7-м классе. Может есть более простое решение? Некоторые родители в комментариях предлагают решать задачу методом подбора значений. Но, как по мне, это больше похоже на гадание, чем на решение.

Посмотрим на наши фигуры еще раз. На первых трех рисунках у нас два квадрата, два круга и два треугольника. Всё это в сумме дает 54. Значит половина — квадрат круг и треугольник равна 27 (54 : 2 = 27).

Или по-другому: круг плюс квадрат 10, а треугольник плюс квадрат 24, значит треугольник на 14 килограмм тяжелее круга. То есть, если круг принять за х, то треугольник равен х + 14. Тогда х + х + 14 = 20; х = 3, и так далее.

Катя и 4 открытки

Эту задачку я обнаружил в заданиях, которые моему сыну-третьекласснику предстояло выполнять на летних каникулах. Это, конечно, не бином Ньютона, но как обойтись без уравнений и только методами начальной школы? Да и много ли детей смогут решить такое без папы, который «силен в математике»?

Без переменных опять не получается. Положим, что первая открытка стоила a рублей, вторая — b, третья — с, четвертая — d. Тогда b+c+d=42; a+c+d=40; a+b+d=38; a+b+c=36. Что теперь делать с этим богатством?

Ясно, что нужно что-то складывать, но не очень понятно, что с чем и на каком основании. Допустим, мы сложили все левые части наших выражений. Получается 3а+3b+3c+3d или 3(a+d+c+d). Можно заметить, что это утроенная сумма стоимости всех открыток. Отсюда находим ее значение (42+40+38+36):3=52 рубля.

Теперь уже дело техники. 52-42=10 — первая открытка; 52-40=12 — вторая открытка; 52-38=14 — третья открытка; 52-36=16 — четвертая открытка. Отметим, что в комментариях умные взрослые с двумя высшими предлагают «нарисовать простой линейный график», «решать методом ненаучного тыка», «чаще подходить к домашке, задача, мол, и яйца выеденного не стоит».

А как ты считаешь, такие задачи помогают ученикам младших классов развивать логику или напрочь отбивают желание учиться? Взрослый-то их решит легко, но сможет ли объяснить ребенку? Ребенок раз не решит, два не решит и сделает вывод, что никогда не сможет понять эту ужасную математику. А мама вздохнет и скажет: «Что поделаешь, мой ребенок — гуманитарий, ему не дано…»

Видео:Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Треугольник вписанный в окружность

Видео:Запомни: все формулы для площади треугольникаСкачать

Определение

Треугольник, вписанный в окружность — это треугольник, который
находится внутри окружности и соприкасается с ней всеми тремя вершинами.

На рисунке 1 изображена окружность, описанная около
треугольника и окружность, вписанная в треугольник.

ВD = FC = AE — диаметры описанной около треугольника окружности.

O — центр вписанной в треугольник окружности.

Видео:Площадь треугольника. Как найти площадь треугольника?Скачать

Формулы

Радиус вписанной окружности в треугольник

r — радиус вписанной окружности.

1. Радиус вписанной окружности в треугольник,
   если известна площадь и все стороны:

Радиус вписанной окружности в треугольник,
если известны площадь и периметр:

Радиус вписанной окружности в треугольник,
если известны полупериметр и все стороны:

Радиус описанной окружности около треугольника

R — радиус описанной окружности.

1. Радиус описанной окружности около треугольника,
   если известна одна из сторон и синус противолежащего стороне угла:

Радиус описанной окружности около треугольника,
если известны все стороны и площадь:

Радиус описанной окружности около треугольника,
если известны все стороны и полупериметр:

Площадь треугольника

S — площадь треугольника.

1. Площадь треугольника вписанного в окружность,
   если известен полупериметр и радиус вписанной окружности:

Площадь треугольника вписанного в окружность,
если известен полупериметр:

Площадь треугольника вписанного в окружность,
если известен высота и основание:

Площадь треугольника вписанного в окружность,
если известна сторона и два прилежащих к ней угла:

Площадь треугольника вписанного в окружность,
если известны две стороны и синус угла между ними:

[ S = fracab cdot sin angle C ]

Периметр треугольника

P — периметр треугольника.

1. Периметр треугольника вписанного в окружность,
   если известны все стороны:
   

Периметр треугольника вписанного в окружность,
если известна площадь и радиус вписанной окружности:

Периметр треугольника вписанного в окружность,
если известны две стороны и угол между ними:

Сторона треугольника

a — сторона треугольника.

1. Сторона треугольника вписанного в окружность,
   если известны две стороны и косинус угла между ними:

Сторона треугольника вписанного в
окружность, если известна сторона и два угла:

Средняя линия треугольника

l — средняя линия треугольника.

1. Средняя линия треугольника вписанного
   в окружность, если известно основание:
   

Средняя линия треугольника вписанного в окружность,
если известныдве стороны, ни одна из них не является
основанием, и косинус угламежду ними:

Высота треугольника

h — высота треугольника.

1. Высота треугольника вписанного в окружность,
   если известна площадь и основание:

Высота треугольника вписанного в окружность,
если известен сторона и синус угла прилежащего
к этой стороне, и находящегося напротив высоты:

[ h = b cdot sin alpha ]

Высота треугольника вписанного в окружность,
если известен радиус описанной окружности и
две стороны, ни одна из которых не является основанием:

Видео:Построение равностронего треугольника.Скачать

Свойства

• Центр вписанной в треугольник окружности
  находится на пересечении биссектрис.
• В треугольник, вписанный в окружность,
  можно вписать окружность, причем только одну.
• Для треугольника, вписанного в окружность,
  справедлива Теорема Синусов, Теорема Косинусов
  и Теорема Пифагора.
• Центр описанной около треугольника окружности
  находится на пересечении серединных перпендикуляров.
• Все вершины треугольника, вписанного
  в окружность, лежат на окружности.
• Сумма всех углов треугольника — 180 градусов.
• Площадь треугольника вокруг которого описана окружность, и
  треугольника, в который вписана окружность, можно найти по
  формуле Герона.

Видео:Три типа формообразования. Основа Сакральной Геометрии. Круг, Треугольник и Квадрат.Скачать

Доказательство

Около любого треугольника, можно
описать окружность притом только одну.

окружность и треугольник,
которые изображены на рисунке 2.

окружность описана
около треугольника.

1. Проведем серединные
   перпендикуляры — HO, FO, EO.
2. O — точка пересечения серединных
   перпендикуляров равноудалена от
   всех вершин треугольника.
3. Центр окружности — точка пересечения
   серединных перпендикуляров — около
   треугольника описана окружность — O,
   от центра окружности к вершинам можно
   провести равные отрезки — радиусы — OB, OA, OC.

окружность описана около треугольника,
что и требовалось доказать.

Подводя итог, можно сказать, что треугольник,
вписанный в окружность — это треугольник,
в котором все серединные перпендикуляры
пересекаются в одной точке, и эта точка
равноудалена от всех вершин треугольника.

🎥 Видео

Всё про углы в окружности. Геометрия | МатематикаСкачать

Мастер-класс "Использование блоков Дьенеша в работе с детьми дошкольного возраста"Скачать

Геометрия Задача найти центр круга /math and magicСкачать

ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать

Треугольник и окружность #shortsСкачать

Учим Геометрические фигуры Круг Квадрат Треугольник Прямоугольник Овал Ромб. Learn Geometric shapesСкачать

Проверь свои знания по математике за 11 классСкачать

Длина окружности. Площадь круга - математика 6 классСкачать

Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Окружность вписана в равнобедренный треугольник. Найти её радиус.Скачать

Круг размером с дваСкачать

Думала не справлюсь😂 #shortsСкачать

ТРИГОНОМЕТРИЯ | Синус, Косинус, Тангенс, КотангенсСкачать