Кривизна прямой и окружности

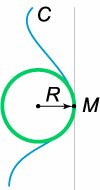
Кривизну кривой можно определить как отношение угла поворота касательной (Delta varphi ) к длине пройденной дуги (Delta s = M.) Такое отношение (largefrac<><>normalsize) называется средней кривизной дуги кривой . Когда точка () приближается к точке (M,) мы получаем кривизну кривой в точке (M:) [k = limlimits_ frac<><> = frac<><>.] Ясно, что кривизна (k) в общем случае может быть как положительной, так и отрицательной, в зависимости от направления вращения касательной.

Если кривая задана своим радиусом вектором (mathbfleft( t right),) ее кривизна определяется формулой [k = frac <<mathbftimes mathbf>><<<<left| <mathbf> right|>^3>>>,] где (mathbf’,) (mathbf») − первая и вторая производные радиус-вектора. В этой формуле в числителе записано векторное произведение векторов (mathbf’) и (mathbf».)

При параметрическом задании координат кривой (xleft( t right)) и (yleft( t right)) формула для расчета кривизны принимает вид [k = frac<> <<<<left[ <<<left( right)>^2> + <<left( right)>^2>> right]>^<largefracnormalsize>>>>.] Если плоская кривая задана явной функцией (y = fleft( x right),) кривизна кривой вычисляется по формуле [k = frac<> <<<<left[ <1 + <<left( right)>^2>> right]>^<largefracnormalsize>>>>.] В случае, когда кривая задана в полярных координатах в виде (rho = rho left( varphi right),) ее кривизна (k) будет определяться выражением [kleft( varphi right) = frac <<+ 2 <<left( right)>^2> — rho rho »>> <<<<left[ <+ <<left( right)>^2>> right]>^<largefracnormalsize>>>>.] Под кривизной кривой часто понимается абсолютное значение кривизны, без учета направления вращения касательной. В таком случае приведенные выше формулы остаются верными, но в числителе появляется модуль. Например, формула кривизны при параметрическом задании координат кривой (xleft( t right)) и (yleft( t right)) будет выглядеть так : [k = frac <<left| right|>> <<<<left[ <<<left( right)>^2> + <<left( right)>^2>> right]>^<largefracnormalsize>>>>] Величина, обратная кривизне, называется радиусом кривизны : [R = frac<>.] Окружность с таким радиусом и центром, расположенном на главной нормали , будет наилучшим образом аппроксимировать плоскую кривую в данной точке (рисунок (2)).

Пусть прямая задана явным уравнением (y = ax + b,) где (a, b) − некоторые коэффициенты. Вычислим кривизну (k) и радиус кривизны (R) данной прямой.

Абсолютное значение кривизны вычисляется по формуле [k = frac <<left| right|>> <<<<left[ <1 + <<left( right)>^2>> right]>^<largefracnormalsize>>>>.] В нашем случае: [y’ = left( right) = a,;;y» = a’ = 0.] Отсюда сразу следует, что кривизна прямой равна нулю, а радиус кривизны, соответственно, равен бесконечности.

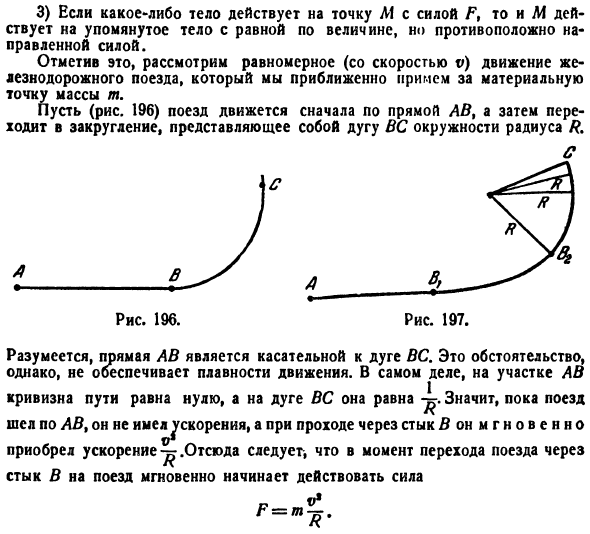
Как известно, при движении тела массой (m) со скоростью (v) вдоль кривой возникает центробежная сила , величина которой зависит от радиуса кривизны (R:) [F = frac<<m>>.] Центробежная сил будет оставаться постоянной в случае, когда тело (например, поезд) движется по дуге окружности. Чтобы исключить резкие толчки при переходе от прямолинейного движения к круговому, используют специальные переходные участки, где кривизна постепенно и равномерно нарастает от (0) до конечного значения (largefracnormalsize.) На таких переходных кривых центробежная сила также будет изменяться равномерно.

Пусть переходная кривая соответствует дуге (OP) (рисунок (3)), длина которой равна (L.) При движении точки (M) вдоль этой кривой радиус кривизны изменяется пропорционально пройденному пути (s:) [frac = ms,] где (m) − коэффициент пропорциональности. Данный коэффициент легко найти из граничного условия: при (s = OP = L) кривизна станет равной (largefracnormalsize:) [frac = mL,;; Rightarrow m = frac<>.] Тогда условие для переходной кривой можно записать в виде следующего уравнения: [ <k = frac = frac<>,>;; <Rightarrow frac<> <<<<left[ <1 + <<left( right)>^2>> right]>^<largefracnormalsize>>>> = frac<>.> ] Решение задачи упрощается, если приблизительно положить (s = x,) где (x) − проекция точки (M) на ось (Ox.) При этом производная (y’) также будет мала и мы можем пренебречь ей в формуле для расчета кривизны. В результате получаем следующее дифференциальное уравнение переходной кривой : [y» = frac<>.] Дважды интегрируя, находим общее решение уравнения: [ <y' = frac<<>><> + ,>;; <y = frac<<>><> + x + .> ] Учитывая начальные условия (yleft( right) = 0) и (y’left( right) = 0,) получаем окончательное уравнение переходной кривой : [y = frac<<>><>,] которая, как видно, является кубической параболой .

Пусть кривая задана уравнением (y = yleft( x right).) Ее радиус кривизны определяется формулой [R = frac<> = frac <<<<left[ <1 + <<left( right)>^2>> right]>^<largefracnormalsize>>>> <<left| right|>>.] Поскольку по условию задачи радиус является постоянной величиной (R = text,) получаем следующее дифференциальное уравнение: [frac <<left| right|>> <<<<left[ <1 + <<left( right)>^2>> right]>^<largefracnormalsize>>>> = frac.] Сделаем замену (y’ = p) и понизим порядок уравнения: [frac <<left|

right|>><<<<left[ <1 +

> right]>^<largefracnormalsize>>>> = frac.] Разделяя переменные и раскрывая модуль, получаем [int <frac<><<<<left( <1 +

> right)>^<largefracnormalsize>>>>> = pm int <frac<>> .] Применим еще одну подстановку: [

;; ;; <dz = frac<><<1 +

>>.> ] Следовательно, уравнение принимает вид [int <frac<><<sqrt <1 + <^2>z> >>> = pm int <frac<>> .] Вспоминая тригонометрическое тождество [1 + z = frac<<<^2>z>>,] данное уравнение можно упростить и затем проинтегрировать: [ <int = pm int <frac<>> ,>;; <Rightarrow sin z = pm fracleft( <x + > right),> ] где () − постоянная интегрирования.

Видео:Кривизна траекторииСкачать

Радиус кривизны плоской кривой

Любая линия является кривой, даже прямая. Поэтому к любой линии применимы такие характеристики как кривизна или радиус кривизны. Как правило кривизна обозначается латинской литерой k, а радиус кривизны греческой литерой ρ.

Между собой эти характеристики кривой связаны следующим образом:

k = 1/ρ (542.1)

Т.е. чем больше радиус кривой, тем меньше ее кривизна.

А теперь рассмотрим несколько частных случаев кривых.

Видео:Взаимное расположение окружности и прямой. 7 класс.Скачать

Радиус кривизны окружности

Окружность — это плоская кривая с постоянным радиусом кривизны. Т.е. радиус окружности это и есть радиус кривизны окружности:

Как определить радиус окружности, мы рассмотрим ниже.

Видео:радиус кривизныСкачать

Кривизна дуги

Любая дуга — это часть окружности. Соответственно радиус дуги равен радиусу окружности:

Рисунок 542.1. Дуга — часть окружности

На рисунке 542.1 мы видим дугу АВ, показанную оранжевым цветом, являющуюся частью окружности с радиусом R. Кроме того, мы видим, что угол α, образованный радиусами в точках А и В, равен углу между касательными (показаны фиолетовым цветом) к окружности в этих точках.

Эти закономерности позволяют определить радиус дуги и найти центр окружности даже тогда, когда изначально мы окружность не видим, а только имеем дугу.

Понятие кривизны дуги формулируется так:

Кривизна дуги — это отношение угла между касательными, проведенными в начале и конце дуги, к длине дуги

Т.е. зная длину дуги m и угол α между касательными, мы можем определить кривизну дуги:

А так как длина дуги зависит от угла между радиусами или между касательными в концах дуги:

то, подставив значение длины дуги в уравнение (542.3), получим:

Примечание: При измерении угла между касательными не в радианах, а в градусах уравнение длины дуги имеет другой вид:

но сути дела это не меняет. Такая запись по-прежнему означает, что мы рассматриваем часть длины окружности. Так при α = 360° дуга становится окружностью

Более того, сама идея радианов на этой формуле и основана, так прямой угол 90° = П/2, развернутый 180° = П и т.д.

И еще одно интересное свойство дуги: Если соединить точки А и В прямой линией, то угол между этой линией и касательными будет равен α/2, а сама прямая линия — это и есть расстояние между точками А и В. Если дуга расположена в плоскости соответствующим образом, например так, как показано на рисунке 542.2:

Рисунок 542.2. Дуга из точки начала координат.

то расстояние между точками — это проекция l дуги на ось х. А максимальное расстояние между дугой и осью х — это стрела дуги h.

Видео:8 класс, 31 урок, Взаимное расположение прямой и окружностиСкачать

Радиус кривизны прямой линии

Любая прямая линия, даже бесконечно длинная, может рассматриваться как бесконечно малая часть окружности, т.е. как дуга. Соответственно в каких единицах измерять радиус такой окружности даже трудно представить.

Поэтому обычно прямой линией называют кривую с бесконечно большим радиусом:

k_п.л = 1/∞ = 0 (542.6)

Про до сих пор неразрешенный парадокс, возникающий при подобных подходах к прямой линии и к окружности, я уже упоминал в статье «Основы геометрии. Определения основных элементов, пятый элемент». Здесь лишь добавлю, что через прямую линию можно провести бесконечное множество плоскостей и в любой из этих плоскостей радиус кривизны прямой линии будет равен бесконечности. При этом через окружность можно провести две взаимно перпендикулярные плоскости, в одной из которых окружность будет окружностью, а в другой — прямой линией конечной длины. Поэтому

все линии, которые в одной из плоскостей имеют бесконечно большой радиус кривизны, считаются плоскими

Ну и на закуску еще несколько парадоксов, на этот раз связанных с определениями кривизны и радиуса:

1. Из уравнения (542.1) можно сделать вывод, что:

kp = 1 (542.7)

Соответственно для прямой линии:

0·∞ = 1 (542.7.2)

Т.е. если бесконечно много раз взять ноль, то на единичку мы наскребем. Впрочем дальше будет еще веселее.

2. Если прямая — это дуга с бесконечно большим радиусом, соответственно касательные, проведенные в концах такой дуги, совпадают с прямой, а угол, образованный касательными, равен нулю.

Это означает, что радиусы проведенные в концах дуги — прямой линии, являются параллельными прямыми и не могут пересекаться. А между тем по определению это радиусы, которые обязательно должны сходиться в некоторой точке — центре окружности.

Получается, что параллельные прямые пересекаться не должны, но где-то в бесконечности все-таки пересекаются.

Разрешить этот парадокс пытались многие математики, однако в пределах евклидовой геометрии при принятом толковании определений данный парадокс не разрешим.

Видео:Пенской А.В. - Классическая дифференциальная геометрия.Семинары - 1. КривизнаСкачать

Радиус кривизны точки

Точка — это самый простой и самый сложный элемент геометрии. Одни считают, что точка не имеет размеров, а значит и определить кривизну или радиус кривизны точки не возможно. Другие, в частности Евклид, считают, что точка не имеет частей, а каковы при этом размеры точки — не совсем понятно. Я же считаю, что точка — это начальный, далее не делимый элемент геометрии, размеры которого пренебрежимо малы по сравнению с остальными рассматриваемыми элементами. В этом случае для точки будут справедливыми следующие уравнения кривизны и радиуса кривизны:

k_т. = 1/0 = ∞ (542.9)

И хотя нас с первых лет обучения в школе учат, что делить на 0 нельзя и даже встроенный в операционную систему калькулятор пишет, что «деление на ноль невозможно», тем не менее делить на ноль можно, а результатом деления всегда будет бесконечность.

Как и в случае с прямой мы имеем парадоксальный результат, выражаемый формулой (542.5.2). Тем не менее точку также можно отнести к плоской кривой, имеющей постоянный радиус кривизны.

Примечание: На мой взгляд большинство из описанных выше парадоксов возникают из-за неправильного толкования понятия «бесконечность». Бесконечность как некая абсолютная величина не имеет пределов, а значит и никакому измерению не поддается. Кроме того бесконечность — это даже не постоянная, а переменная величина. Например луч — это прямая линия с началом в некоторой точке. Длина луча может быть бесконечно большой. При этом прямая линия тоже может быть бесконечно длинной при этом не иметь ни начала ни конца. Получается, что с одной стороны бесконечно длинный луч вроде бы в 2 раза короче, чем бесконечно длинная прямая. А с другой стороны длины их бесконечны и поэтому равны.

Возможным выходом из этой ситуации является принятие понятия «бесконечность», как относительного. Например, кривизна прямой линии является пренебрежимо малой величиной по отношению к радиусу кривизны. Или радиус кривизны прямой линии несопоставимо больше кривизны. Подобные толкования допускают и наличие кривизны прямой и некое конечное значение радиуса кривизны прямой и многое другое. Я бы назвал такой относительный подход к рассмотрению проблемы реалистичным, а подходы, использующие абсолютные понятия — идеализированными. Впрочем прямого отношения к теме данной статьи это не имеет. Продолжим рассмотрение плоских кривых.

И окружность и прямая линия являются плоскими кривыми с постоянным радиусом кривизны. При этом радиус кривизны прямой линии всегда известен, так как равен бесконечности, а для окружности всегда можно определить радиус, воспользовавшись теоремой Пифагора. Так в частном случае, если центр окружности совпадает с началом координат рассматриваемой плоскости (u = 0; v = 0 — координаты центра окружности), то:

Рисунок 541.4. Радиус окружности, как гипотенуза прямоугольного треугольника.

R 2 = x 2 + y 2 (541.1.2)

А в общем случае, когда координаты центра окружности не совпадают с началом координат:

Рисунок 542.3. Окружность, центр которой не совпадает с началом координат.

R 2 = (x — u) 2 + (y — v) 2 (542.10)

Но в жизни достаточно часто приходится сталкиваться с кривыми, радиус кривизны которых — не постоянная величина. Более того, этот радиус может изменяться в двух плоскостях измерения. Тем не менее так далеко углубляться в геометрию и алгебру мы не будем и далее рассмотрим, как можно определить радиус плоской кривой в некоторой точке.

Видео:Кривизна кривой и главная нормальСкачать

Плоские кривые с изменяющимся радиусом кривизны

Примеров плоских кривых с изменяющимся радиусом кривизны очень много, это и гиперболы, и параболы, и синусоиды и т.п. Определение радиуса кривизны таких кривых основано на следующих теоретических предпосылках:

1. Любую окружность можно рассматривать как некоторое множество дуг.

2. Если количество дуг, составляющих окружность, стремится к бесконечности, то соответственно длина таких дуг стремится к нулю (m → 0).

3. Если мы обозначим длину такой очень короткой дуги как приращение функции длины окружности (m = Δl), то уравнение кривизны (542.3) примет следующий вид:

(542.3.1)

4. Тогда любую плоскую кривую с изменяющимся радиусом можно рассматривать как стремящееся к бесконечности множество дуг с постоянным радиусом. Другими словами в пределах любой кривой, описываемой параметрическими уравнениями, всегда можно выделить дугу, пусть даже и очень малой длины, стремящейся к точке и определить для нее кривизну и радиус кривизны в рассматриваемой точке.

Это означает, что самый точный способ определения радиуса кривизны в таком случае — это использование дифференциальных исчислений. В общем случае для этого нужно два раза продифференцировать уравнение радиуса окружности (542.10) по аргументу функции х, а затем извлечь квадратный корень из полученного результата. В итоге (полный вывод уравнения здесь не привожу из-за повышенной сложности записи, а для особо заинтересованных есть справочники и другие сайты) мы получим следующую формулу для определения радиуса кривизны:

(542.11)

Соответственно кривизна плоской кривой в рассматриваемой точке будет равна:

(542.12)

В частном случае, когда тангенс угла между касательными — первая производная от функции — является относительно малой величиной, например, tg2° = 0.035 соответственно (tg2°) 2 = 0.0012, то влиянием куба суммы первой производной и единицы на кривизну можно пренебречь (значение знаменателя дроби сводится к единице) и тогда:

k = y» = d 2 y/dx 2 (542.12.2)

Т.е. формально в таких случаях кривизной считается не отношение угла наклона между касательными к длине дуги, а некоторая величина, примерно соответствующая высоте h на рисунке 542.2.

Эта особенность второй производной очень активно используется в частности для упрощения определения прогиба элементов строительных конструкций.

На этом пока все.

Доступ к полной версии этой статьи и всех остальных статей на данном сайте стоит всего 30 рублей. После успешного завершения перевода откроется страница с благодарностью, адресом электронной почты и продолжением статьи. Если вы хотите задать вопрос по расчету конструкций, пожалуйста, воспользуйтесь этим адресом. Зараннее большое спасибо.)). Если страница не открылась, то скорее всего вы осуществили перевод с другого Яндекс-кошелька, но в любом случае волноваться не надо. Главное, при оформлении перевода точно указать свой e-mail и я обязательно с вами свяжусь. К тому же вы всегда можете добавить свой комментарий. Больше подробностей в статье «Записаться на прием к доктору»

Для терминалов номер Яндекс Кошелька 410012390761783

Номер карты Ymoney 4048 4150 0452 9638 SERGEI GUTOV

Для Украины — номер гривневой карты (Приватбанк) 5168 7422 4128 9630

Категории:

• Расчет конструкций . Основы прикладной геометрии

Оценка пользователей:10.0 (голосов: 1)Переходов на сайт:6701Комментарии:

Примечание: Возможно ваш вопрос, особенно если он касается расчета конструкций, так и не появится в общем списке или останется без ответа, даже если вы задатите его 20 раз подряд. Почему, достаточно подробно объясняется в статье «Записаться на прием к доктору» (ссылка в шапке сайта).

Видео:9 класс, 6 урок, Уравнение окружностиСкачать

Кривизна

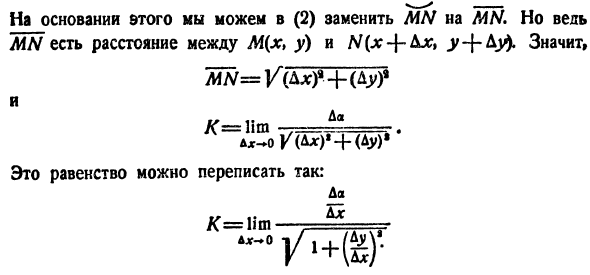
Видео:Радиус кривизны траекторииСкачать

Кривизна

• Кривизна Н°1.Средняя и истинная кривизна. Здесь вы познакомитесь с кривизной, которая является важной характеристикой кривой. Искривление линии является мерой степени кривизны этой линии. Возьмем линию L (рис. 186).Она сама действует как касательная в каждой точке. Поэтому, когда вы извлекаете любой отрезок AB из L,

касательные L в точках A и B совпадают. Это может быть выражено в том, что направление линии не изменяется при переходе от одной точки линии к другой. another. в точках A и B кривой линии L Я Л Рисунок

In в случае кривых это не так. Если (рис. 187) нарисуйте Людмила Фирмаль

186.187. Если они касательные, то образуют определенный угол 0.Можно сказать, что при переходе от A к B касательная к L (и сама кривая L) стала углом b. величина этого угла поворота Дайте представление о степени кривизны L дуги AB: чем больше угол 0, тем сильнее будет изгибаться L, но само значение угла b еще не работает как мера описанной кривизны above. In дело в том, что если линия

L в сечении длиной 100 см повернута на 50°, или если такой же угол повернут в сечении длиной 200 см, то это уже 1.А 2-й-в половине). Таким образом, значение угла b само по себе не важно, но процент этого угла является средним на единицу длины Дуги Ab. Эти

• соображения приводят к следующим определениям: Средняя кривизна дуги AB линии определения L равна отношению угла 0.Это заставляет касательную L вращаться. При переходе от A к B, вплоть до длины дуги AB Замечание. 1) в Формуле (1) знак угла 0 не учитывается. Угол берется в абсолютном значении. Поэтому средняя кривизна не всегда

отрицательна. 2) единицей измерения угла при расчете КСР всегда является Радиан).Поскольку имя угла опущено в выражении, которое отображает угол в радианах、 Один 188. ** Размер кривизны Длина 1) угол 0, описанный выше, иногда называют углом смежности

(по неизвестным причинам) дуги AJ. Людмила Фирмаль

Нетрудно понять, что одна и та же кривая в разных сечениях может иметь разные средние кривизны(как предполагает сам термин средние кривизны). Таким образом, средняя кривизна дуги АВ рис. 188、 PQ arc. To охарактеризуйте кривизну линии L в заданной точке M, введите: Определение истинная кривизна линии L в нижней точке M является

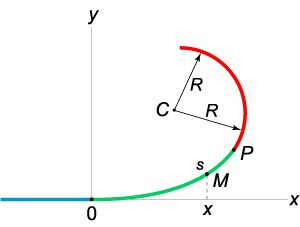
пределом средней кривизны бесконечно малой дуги, которая сжимается до точки M. Однако обычно прилагательное «истинный» опускается, что просто представляет кривизну линии L в точке M. н°2.Формула расчета кривизны. Спросил. Найти истинную кривизну K кривой y = f(x) в заданной точке M (x, y). Решение. Возьмите другую точку кривой, чем M+>+.Угол, образованный

касательной и осью Ox кривой, зависит от абсциссы точки контакта. Пусть значение этого угла в точках M и N равно a и a соответственно — <- yes. Из рисунка видно, что угол, на который поворачивается касательная при переходе из 189 точки M в точку N, 0,

равен внутреннему углу треугольника ABC C. другой внутренний угол этого треугольника (угол A） СК и-Ж-Д ® — внешний угол одного треугольника, не смежных с и С. Таким образом,= 0 +здесь 0 =Да. Таким образом, средняя кривизна дуги у нас равна К-АА Истинная кривизна, K, является пределом этого уравнения. Точка N-это М,

то есть когда Ах да Рисунок 189. Ноль： Нш ™ (2) Ш Чтобы найти это ограничение, рассмотрим следующее:1) BX-Если+ 0, то дробь Да. — R-неопределенность В Да. Нравится 2) при раскрытии такой неопределенности молекула и замещение могут быть заменены эквивалентным значением. 3) крошечная дуга эквивалентна

строке*)： Исходя из этого, вы можете заменить WE на MN в (2).Но понятие MN-это расстояние между M(x, y) и N (x-f-Ajc, y-f-Ay).Значение Ж = +(ДУ) 1 К = им K (4ds) » +(Au) ’это равенство может быть переписано как: Да. К = Лим— = м = (Ничто не мешает вам

рассматривать Ajc> 0, но это вовсе не проблема, потому что в выражении K она касается только абсолютного значения этого выражения.) К АС.#. АА ээ£ = г * > БВ и = * Х- Значение (3） помните, что это tga = y’X. дайте 0, поэтому перед радикалом нужно выбрать символ -> -.Таким образом, y = YR -««• — Jq не. Следовательно, Vx = — rr = t. вторая производная дает V ^ x. знак минуспоследнего выражения

отбрасывается, так как y’X должно быть получено только в абсолютных значениях. Тогда из простого преобразованного выражения(4) (6） К-5-、 То есть кривизна окружности во всех ее точках одинакова и равна единице, объединенной радиусом

окружности*). П°3.Для параметрических заданий. Кривая задается параметрическим уравнением (7 )） йк = СР(0, мл = Т (Ф + ryi» Образцы. Найти кривизну кривой r = * A, где r ’= r «=I. n°b. окружности, центры и радиусы кривизны. Малую дугу кривой линии L можно почти заменить отрезком линии, касательной к L в определенной точке рассматриваемой дуги. Если есть интерес к длине дуги или

ее направлению, такая замена допускается. Однако кривизна прямой линии равна нулю, поэтому она явно неприемлема при исследовании кривизны дуги. Если вы хотите грубо заменить дугу кривой L дугой более простой линии, проблема, связанная с кривизной линии L, требует, чтобы вы взяли что-то вместо линии замены. 191 и более. Очень естественный Нарисуйте круг для этой цели. Когда эти

соображения развиваются, мы приходим к следующему определению: определение. Окружность кривизны кривой L в данной точке M является окружностью(рис. 191） 1) пройти через точку M 2) M имеет общую связь с C 3) кривая в точке M с той же кривизной K, что и L. 4) Центр C на стороне кривой L. кривая L вращается своей вогнутой

поверхностью (точка M).Давайте рассмотрим это поближе definition. As для кривизны кривой L мы упомянули, что мы говорим о кривизне точки Af, потому что в любой кривой кривизна отличается от точки к точке. Поскольку кривизна окружности во всех точках одинакова, мы не говорили, что она означает кривизну в точке M, как для

окружности кривизны. Кроме того, поскольку окружность касается кривой L в точке M, ее центр C является нормалью кривой L в точке M. радиус кривизны окружности R можно легко вычислить, каким он должен быть. То есть, с одной стороны, кривизна этой окружности должна быть равна кривизне K линии L в точке

M. Кривизна является i. So f(= 4-и (13 )） Это значение называется радиусом кривизны кривой L в точке M(так как в разных точках радиус кривизны кривой L разный, нужна ссылка на точку! это не. Кроме того, центр C окружности кривизны называется центром кривизны кривой L в точке Af. Конечно, все вышесказанное применимо, когда точка M не является прямой точкой кривой

L. In в этом последнем случае K = 0, и нет круга с такой кривизной. Условно, в точке линеаризации кривой L окружность кривизны вырождается в прямую линию (то есть становится касательной L в рассматриваемой точке).Поэтому говорят, что в точке коррекции,

радиус кривизны равен бесконечности, а центр кривизны удаляется до бесконечности. Образцы. Построить центр кривизны параболы Один Его вершины(0, 0). Из уравнения линии высвобождения материала, yx = x, yx = 1• Итак, K = — tm. И если x = 0, то можно видеть, что K = 1.И так оно и есть.、 (+икс’ )* » (13) к R = 1.In кроме того, поскольку парабола вершины является касательной к оси Ox, центр кривизны C находится на оси Oy и выше Ox axis. So, центр окружности

кривизны равен C (0, 1), а радиус равен R = 1. 192 вы можете видеть, насколько близки парабола и ее окружность кривизны друг к другу. Учитывая малую дугу кривой U, содержащей точку Af, можно приблизительно считать, что эта дуга является дугой окружности кривизны(линия L точки Af).Поэтому мы снимаем вышеупомянутую

дугу в другой точке N, которая отличается от Af, но потому, что она очень близка к Af (потому что дуга должна быть маленькой!).), Af и N можно считать находящимися на одной окружности в контакте с кривыми L и Af (точно) и N (приблизительно).Однако центр C этой окружности должен находиться непосредственно на 2 нормалях I, нарисованных через Af и M, то есть точках пересечения этих

нормалей. Это соображение не только обеспечивает относительно простой способ нахождения центра с чертежа приблизительно, но и приводит к возможности другого определения центра кривизны. То есть ошибка, возникающая в результате замены дуги кривой на дугу этого круга кривизны, меньше, чем дуга shorter. In другими

словами, если взять точку M на кривой L и точку N рядом с ней и найти точку пересечения нормали, проведенной от Af и M до L, то получится более точный центр кривизны C (точка Af), где N ближе к Af. Поэтому вы можете дать определение. Центром кривизны кривой L в заданной точке Af, C, является предельное положение

пересечения нормали через Af и нормали через бесконечно близкую точку N. Это определение позволяет по-новому продемонстрировать всю теорию кривизны. То есть, поскольку мы знаем, каков центр кривизны кривой L в точке M, мы можем использовать формулу M R = СМ И тогда мы вводим понятие кривизны/ C К = = 7т ’ n°b. концепция

эволюции и involute. In выше мы обратили внимание читателя на то, что говоря о центре кривизны с любой кривой, нам нужно указать, для какой точки м кривой точка С является центром кривизны. Это приводит к следующему определению: Геометрическое положение центра кривизны линии определения L называется вырождением

этой линии. Сама линия L называется эвольвентой ее Эволюта*). Ясно, что прямая линия не имеет Эволюта, а точка является осевой линией circle. In в других случаях некоторые линии служат эволюциями. Образцы. n * 4§ 3 определил понятие эвольвенты в a circle. It показано, что эта линия на самом деле действует как

Эвольвента в введенном смысле, то есть круг действует как ее эволюция. Для этого используйте точку M (t) эвольвенты окружности, чтобы найти нормали, которые проходят через M и достигают involute. As мы видели, что параметрические уравнения эвольвенты являются: х = р (потому что т-ф-1 грех Т), Г = Р(греха Т — * потому t). Отсюда х ’Т = РТ потому t, г’ Ф = #ц НТ. (14） Так… учитывая, что t-угол наклона луча OB к оси Ox (рис. 185), становится ясно, что

касательная к эвольвенте в точке M параллельна радиусу OB, а Нормаль перпендикулярна OB. Но из M можно опустить только 1 перпендикулярно OB, и это поток MB. Таким образом, MB становится искомой нормалью центра кривизны эвольвенты в точке M. Теперь

найдем радиус кривизны эвольвенты. Согласно (8), кривизна эвольвенты равна _ yjx ’ т-г’txi Но из(14) ДГ; = /?(соб * — t sin 0,#=#(sin t + tcost). Если вы назначите это (15)、 — з И. Поэтому радиус кривизны эвольвенты в точке M равен Rtt, то есть длине участка резьбы Mb. It сразу видно из рисунка, что точка B нити накала из окружности

находится на стороне эвольвенты, которая вращается вогнутой, поэтому ясно, что B будет центром эвольвентной кривизны в точке M. поскольку различные положения точки B заполняют окружность, она служит в качестве эвольвенты круга и эвольвенты. Попутно

мы установили, что нормальный MB для эвольвенты связан с эволюцией соответствующего центра кривизны. Ниже показано, что это всегда так. н-7.Координаты центра города curvature. It возникает задача нахождения центра кривизны c координатой (x0 yy) кривой y = f (x) в точке M (x: 0, y0) этой кривой. Решение этой задачи основано

на следующих 2 соображениях: 1) точка C находится на нормали кривой y = f ( * ) через точку M, 2) расстояние от M равно радиусу кривизны/так как точка C находится на нормали кривой y = f ( * ). Нормальные уравнения г-СС^ — • Тогда первое соображение дадим xc — = — Yo (Us —Yo) ’ 2-е рассмотрение、 Где находится радиус

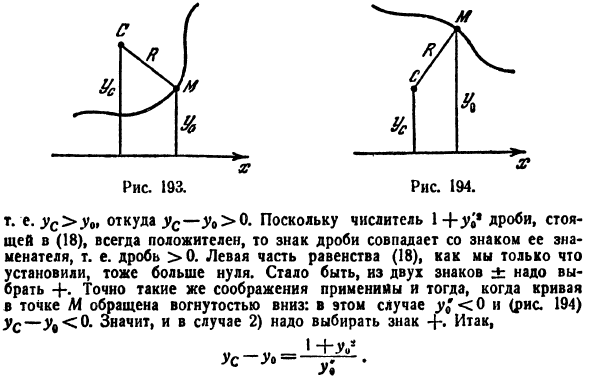
кривизны?(13) и (4). Примите форму (17) (ДГС-ДГ.) ’+(yy-y.) ’=(1 ″ U. здесь подставляется xc-dg, а из (16), pay (Us-A) W +(Us-Y’) ’= (yce + yif, уменьшаясь с ’ Y * 1 Кишащий с-Л -±!±* 5(.Восемь） Вау. Осталось выяснить, какой из 2-х персонажей выбрать. Различают 2 случая.1) кривая y = f(x) в точке M изгибается вверх вогнутой поверхностью, а 2) вогнутой поверхностью изгибается вниз к M. In случай I) V! Понятно,

что там > 0, и далее на рисунке 193 точка С находится выше точки АФ. Рисунок 193.Рисунок 194. То есть yn> y0, а ync-y0> 0. (18) числитель дроби 1 + ^ *всегда положителен, поэтому знак дроби совпадает со знаком знаменателя, то есть дробью> 0.Левая часть уравнения (18), как мы установили ранее, больше нуля. Поэтому вам нужно выбрать

2 символа±.Точно такие же соображения применяются, когда кривая в точке M направлена вогнутой вниз surface. In это дело, y!

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

📸 Видео

Уравнение окружности (1)Скачать

Сопряжение прямой с окружностьюСкачать

Камень брошен горизонтально, надо искать радиус кривизны траектории. (Волькенштейн 1.20)Скачать

Урок 43. Криволинейное движение. Равномерное движение по окружности. Центростремительное ускорениеСкачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

УРАВНЕНИЯ ОКРУЖНОСТИ И ПРЯМОЙ 9 класс геометрияСкачать

Длина окружности. Математика 6 класс.Скачать

Урок 5 Mathcad Определяем кривизну земли при расчете радиорелейной линииСкачать

10.1.10. Радиус кривизны траекторииСкачать

ГЕОМЕТРИЯ 9 класс: Уравнение окружности и прямойСкачать

9 класс, 7 урок, Уравнение прямойСкачать