Котангенс минус корень из 3 на окружности (7 видео)

Значения тангенса и котангенса на тригонометрическом круге

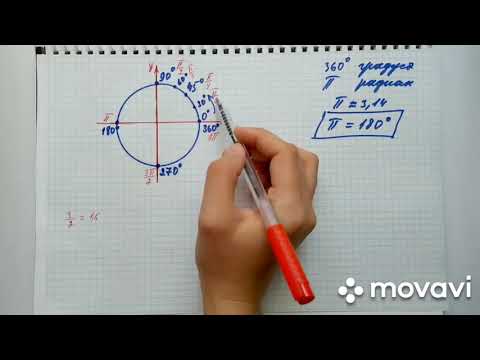
В прошлой статье мы познакомились с тригонометрическим кругом и научились находить значения синуса и косинуса основных углов.

Как же быть с тангенсом и котангенсом ? Об этом и поговорим сегодня.

Где же на тригонометрическом круге оси тангенсов и котангенсов?

Ось тангенсов параллельна оси синусов (имеет тоже направление, что ось синусов) и проходит через точку (1; 0).

Ось котангенсов параллельна оси косинусов (имеет тоже направление, что ось косинусов) и проходит через точку (0; 1).

На каждой из осей располагается вот такая цепочка основных значений тангенса и котангенса: Почему так?

Я думаю, вы легко сообразите и сами. 🙂 Можно по-разному рассуждать. Можете, например, использовать тот факт, что и

Собственно, картинка за себя сама говорит.

Если не очень все же понятно, разберем примеры:

Пример 1.

Вычислить

Находим на круге . Эту точку соединяем с точкой (0;0) лучом (начало – точка (0;0)) и смотрим, где этот луч пересекает ось тангенсов. Видим, что

Ответ:

Пример 2.

Вычислить

Находим на круге . Точку (0;0) соединяем с указанной точкой лучом. И видим, что луч никогда не пересечет ось тангенсов.

не существует.

Ответ: не существует

Пример 3.

Вычислить

Находим на круге точку (это та же точка, что и ) и от нее по часовой стрелке (знак минус!) откладываем (). Куда попадаем? Мы окажемся в точке, что на круге у нас (см. рис.) названа как . Эту точку соединяем с точкой (0;0) лучом. Вышли на ось тангенсов в значение .

Так значит,

Ответ:

Пример 4.

Вычислить

Поэтому от точки (именно там будет ) откладываем против часовой стрелки .

Выходим на ось котангенсов, получаем, что

Ответ:

Пример 5.

Вычислить

Находим на круге . Эту точку соединяем с точкой (0; 0). Выходим на ось котангенсов. Видим, что

Ответ:

Теперь, умея находить по тригонометрическому кругу значения тригонометрических функций (а я надеюсь, что статья, где мы начинали знакомство с кругом и учились вычислять значения синусов и косинусов, вами прочитана…), вы можете пройт и тест по теме «Нахождение значений косинуса, синуса, тангенса и котангенса различных углов».

Чтобы не потерять страничку, вы можете сохранить ее у себя:

Содержание

Тригонометрический круг: вся тригонометрия на одном рисунке
А теперь подробно о тригонометрическом круге:
Котангенс минус корень из 3 на окружности
Шаг 1. Введите неравенство
Решение
Где учитесь?
🎬 Видео

Видео:Как видеть тангенс? Тангенс угла с помощью единичного круга.Скачать

Тригонометрический круг: вся тригонометрия на одном рисунке

Тригонометрический круг — это самый простой способ начать осваивать тригонометрию. Он легко запоминается, и на нём есть всё необходимое.
Тригонометрический круг заменяет десяток таблиц.

Вот что мы видим на этом рисунке:

Перевод градусов в радианы и наоборот. Полный круг содержит градусов, или радиан.

Значения синусов и косинусов основных углов. Помним, что значение косинуса угла мы находим на оси , а значение синуса — на оси .

И синус, и косинус принимают значения от до .

Значение тангенса угла тоже легко найти — поделив на . А чтобы найти котангенс — наоборот, косинус делим на синус.

Знаки синуса, косинуса, тангенса и котангенса.

Синус — функция нечётная, косинус — чётная.

Тригонометрический круг поможет увидеть, что синус и косинус — функции периодические. Период равен .

Видео:Тригонометрическая окружность. Как выучить?Скачать

А теперь подробно о тригонометрическом круге:

Нарисована единичная окружность — то есть окружность с радиусом, равным единице, и с центром в начале системы координат. Той самой системы координат с осями и , в которой мы привыкли рисовать графики функций.

Мы отсчитываем углы от положительного направления оси против часовой стрелки.

Полный круг — градусов.
Точка с координатами соответствует углу ноль градусов. Точка с координатами отвечает углу в , точка с координатами — углу в . Каждому углу от нуля до градусов соответствует точка на единичной окружности.

Косинусом угла называется абсцисса (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .

Синусом угла называется ордината (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .

Всё это легко увидеть на нашем рисунке.

Итак, косинус и синус — координаты точки на единичной окружности, соответствующей данному углу. Косинус — абсцисса , синус — ордината . Поскольку окружность единичная, для любого угла и синус, и косинус находятся в пределах от до :

Простым следствием теоремы Пифагора является основное тригонометрическое тождество:

Для того, чтобы узнать знаки синуса и косинуса какого-либо угла, не нужно рисовать отдельных таблиц. Всё уже нарисовано! Находим на нашей окружности точку, соответствующую данному углу , смотрим, положительны или отрицательны ее координаты по (это косинус угла ) и по (это синус угла ).

Принято использовать две единицы измерения углов: градусы и радианы. Перевести градусы в радианы просто: градусов, то есть полный круг, соответствует радиан. На нашем рисунке подписаны и градусы, и радианы.

Если отсчитывать угол от нуля против часовой стрелки — он положительный. Если отсчитывать по часовой стрелке — угол будет отрицательным. Например, угол — это угол величиной в , который отложили от положительного направления оси по часовой стрелке.

Легко заметить, что

Углы могут быть и больше градусов. Например, угол — это два полных оборота по часовой стрелке и еще . Поскольку, сделав несколько полных оборотов по окружности, мы возвращаемся в ту же точку с теми же координатами по и по , значения синуса и косинуса повторяются через . То есть:

где — целое число. То же самое можно записать в радианах:

Можно на том же рисунке изобразить ещё и оси тангенсов и котангенсов, но проще посчитать их значения. По определению,

Видео:Алгебра 10 класс. 2 октября. Тангенс и котангенс на окружностиСкачать

Котангенс минус корень из 3 на окружности

Видео:Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Шаг 1. Введите неравенство

Укажите решение неравенства: cot(x)>-sqrt(3) (множество решений неравенства)

Решение

Дано неравенство:
$$cot > — sqrt$$
Чтобы решить это нер-во — надо сначала решить соотвествующее ур-ние:
$$cot = — sqrt$$
Решаем:
$$x_ = — frac$$
$$x_ = — frac$$
Данные корни
$$x_ = — frac$$
являются точками смены знака неравенства в решениях.
Сначала определимся со знаком до крайней левой точки:
$$x_ — sqrt$$

значит решение неравенства будет при:
$$x

Видео:Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать