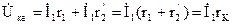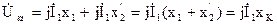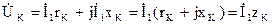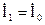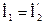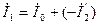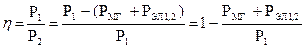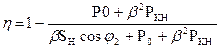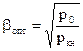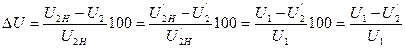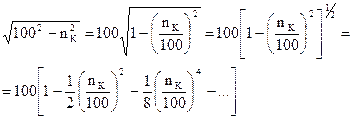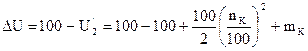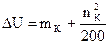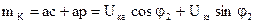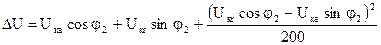а) Назначение нулевого провода.
При несимметричной нагрузке звездой без нулевого провода (на рис. 11.19 ключ разомкнут) сопротивления всех фаз неодинаковы: Z А 

Это напряжение U N, действующее между точками N и N’ (рис. 11.19), показано на рис. 11.20. При любом направлении вектора U N напряжения на фазах нагрузки будут неодинаковы.
При включении и выключении приемников проводимости фаз Y А, Y B и Y C изменяются произвольным образом, это приводит к изменению напряжения смещения нейтрали U N, ведущее, в свою очередь, к произвольному изменению напряжений на фазах нагрузки. Подавляющее большинство электросиловых приемников функционирует только при номинальном питающем напряжении. Поэтому соединение звездой без нулевого провода для несимметричной или изменяемой нагрузки практически не используется вследствие невозможности обеспечить номинальное питающее напряжение. При большом числе приемников, статистически в «среднем» обеспечивающих примерно одинаковую нагрузку фаз, несмотря на включение и выключение отдельных потребителей, смещение нейтрали невелико. Это позволяет использовать соединение звездой без нулевого провода для мощных линий электропередач на трансформаторные подстанции напряжением до 6,3 кВ. Соединение звездой без нулевого провода используется и в устройствах, предназначенных для контроля и анализа режимов трехфазных цепей.
б) Соединение звездой с нулевым проводом.
Для соединения звездой с нулевым проводом (на рис. 11.19 ключ замкнут) определим напряжение нейтрали также по формуле двух узлов:
В реальных системах электроснабжения проводимость нулевого провода Y N много больше проводимостей фаз и практически можно считать, что сопротивление нулевого провода близко к нулю. Тогда при Y N → ∞ знаменатель в выше написанной формуле стремится к бесконечности, U N → 0 и при наличии нулевого провода с достаточно малым сопротивлением смещение потенциала нулевой точки N’ нагрузки отсутствует. На фазах нагрузки независимо от их сопротивлений поддерживаются напряжения, составляющие симметричную трехфазную систему.
Токи фаз нагрузки определяются по закону Ома:

Ток нейтрального провода (см. рис. 11.14) можно определить по первому закону Кирхгофа для узла N’ — рис. 11.22 (на рисунке изображен вспомогательный вектор тока, равный сумме токов I А+ I С):
Чем больше несимметрия фаз нагрузки, тем больше «уравнительный» ток I N нулевого провода.
Соединение звездой с нулевым проводом повсеместно используется для электропитания жилых и общественных зданий, производственных приемников энергии и в других случаях с многочисленными приемниками, включаемыми и выключаемыми независимо друг от друга.

Если пренебречь сопротивлением соединительных проводов, то напряжения на фазах нагрузки равны линейным напряжениям трехфазного источника . Фазные токи при несимметричной нагрузке Z А B 

На рис. 11.25 показана векторная диаграмма токов при несимметричной активной нагрузке. Линейные токи определяются по первому закону Кирхгофа для узлов А, В и С рис. 11.17:
Как видно из векторной диаграммы (рис. 11.25), линейные токи не равны по модулю и смещены по фазе на углы, не равные 120°. В общем случае и фазные токи не равны по модулю и смещены по фазе на углы, не равные 120°.
Векторная диаграмма линейных токов показана на рис. 11.25.
г) Аварийные режимы в трехфазных цепях.
Частными случаями несимметричных режимов являются аварийные режимы в трехфазных цепях: обрывы нейтрального и линейных проводов, КЗ в фазах.
Абсолютно безопасными являются разрывы в фазах нагрузки, соединенной треугольником или звездой с нулевым проводом (отключения фаз)
Аварийными, пожароопасными являются КЗ фаз нагрузки таких соединений. Все другие случаи приводят к резкому изменению номинальных напряжений на фазах нагрузки и могут привести к аварийной ситуации. Обрыв нулевого провода несимметричной звезды был рассмотрен в примере 11.9.
Для соединения трехфазной цепи в звезду возможны следующие аварийные режимы работы:
1) обрыв фазы (рис. 3.10);
2) обрыв нулевого провода (рис. 3.11);
3) короткое замыкание фазы при обрыве нуля (рис. 3.12).
4) обрыв фазы и нуля, рис. 3.12.
Для соединения трехфазной цепи в треугольник возможны следующие аварийные режимы:
2) обрыв линейного провода.
- Аварийные режимы в нагрузках соединенных звездой
- Аварийные режимы в нагрузках соединенных треугольником
- Треугольник короткого замыкания
- Схемы соединений и особенности разомкнутого треугольника трансформатора напряжения
- Схемы соединений трансформаторов напряжения в открытый и разомкнутый треугольник
- Общие сведения
- Различие между соединениями
- Схема полной звезды ТТ
- В каких случаях применяют
- Особенности схем подключения нагрузок к тиристорному регулятору
- Схема неполной звезды ТТ с реле в обратном проводе
- 💥 Видео
Аварийные режимы в нагрузках соединенных звездой
1) При обрыве фазы А 




2) Обрыв нулевого провода не всегда вызывает аварию в трехфазных цепях. Если нагрузка симметрична, то обрыв нулевого провода не изменит токов нагрузок, так как для симметричной нагрузки

Для несимметричных нагрузок 
Для того чтобы показать это, используем метод двух узлов:


3) При коротком замыкании фазы А и обрыве нуля напряжение этой фазы равно нулю:
Нагрузка фазы В увеличится в 

Аналогично и в фазе С:



4) Обрыв фазы и нулевого провода дает:

В оставшихся фазах токи будут одинаковыми, а напряжения на них будут зависеть от сопротивлений нагрузок (рис. 3.16).
 Аварийные режимы в нагрузках соединенных треугольником
Аварийные режимы в нагрузках соединенных треугольником
1) Обрыв фазы.
Ключ к1 замкнут, ключ к2 разомкнут (рис. 3.17). В этом режиме ток в фазе 
2)
Обрыв линейного провода. Ключ к1 разомкнут и ключ к2 замкнут (рис. 3.19). Фаза нагрузки с 

Общие сведения
При коротких замыканиях в фазах нагрузки или между линейными проводами токи резко возрастают и происходит аварийное отключение установки защитой.
Обрывы фаз или линейных проводов при соединении нагрузки в треугольник не приводят к перегрузкам по токам или напряжениям, как это иногда случается при соединении нагрузки в звезду.
При обрыве одной фазы нагрузки (рис. 8.5.1) ток этой фазы становится равным нулю, а в оставшихся двух фазах ток не меняется. Два линейных тока уменьшаются в 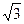
При обрыве линейного провода (например, В) фазные сопротивления RAB и RBC оказываются соединёнными последовательно и включёнными параллельно с сопротивлением RCA на напряжение UCA (рис. 8.5.2). Цепь фактически становится однофазной.

При одновременном обрыве линейного провода и одной фазы нагрузки цепь также становится однофазной (рис. 8.5.3 и 8.5.4).
Экспериментальная часть
Задание
Экспериментально исследовать аварийные режимы трёхфазной цепи при соединении нагрузки в треугольник.
Порядок выполнения работы
· Соберите цепь цепь согласно схеме (рис.8.5.5) с сопротивлениями фаз RAВ=RBС=RCА=1кОм и измерьте линейные и фазные токи в симметричном режиме.
· Проделайте измерения фазных и линейных токов (отличных от нуля) во всех режимах, указанных в табл. 8.5.1. (Измерения токов можно производить одним – двумя амперметрами, переключая их из одной фазы в другую, либо виртуальными приборами).
· По экспериментальным данным постройте векторные диаграммы для каждого аварийного случая в выбранном масштабе.
· Ответьте на контрольные вопросы.
| Режим | IAB, мА | IBC, мА | ICA, мА | IA, мА | IB, мА | IC, мА |
| Симметричный режим, Rф=1 кОм | ||||||
| Обрыв фазы АВнагрузки | ||||||
| Обрыв линейного провода А | ||||||
| Обрыв фазы АВ и линии С | ||||||
| Обрыв фазы АВи линииА |
Векторные диаграммы
- Обрыв фазы АВ нагрузки
Обрыв линейного провода А
3. Обрыв фазы АВ и линии С 4. Обрыв фазы АВ и линии А
Вопрос:Как вычислить мощность несимметричной трёхфазной нагрузки?
Ответ: ……….
Вопрос:Как (во сколько раз) увеличиваются или уменьшаются фазные и линейные токи в каждом из рассмотренных аварийных режимов?
Ответ: ……….
Расчёт и экспериментальное исследование цепи при несинусоидальном приложенном напряжении
(для компьютерного варианта стенда)
Общие сведения
Несинусоидальное периодическое напряжение, приложенное к электрической цепи, можно разложить в ряд Фурье:
Расчёт цепи проводят с использованием принципа наложения в следующей последовательности:
· рассчитывают цепь при постоянном приложенном напряжении U ;
· рассчитывают цепь (обычно комплексным методом) при синусоидальном приложенном напряжении с амплитудой U1m частоты и частотой w (k=1);
· повторяют расчёт при k = 2, 3, 4, …, учитывая, что индуктивные сопротивления увеличиваются с ростом частоты ( 

· переходят к мгновенным значениям и суммируют постоянную и синусоидальные составляющие тока (напряжения) в каждой ветви;
· определяют действующие значения токов и напряжений, а также мощности по формулам:
где Uk, Ik – действующие значения синусоидальных составляющих.
Чем больше гармоник взято для расчёта, тем выше точность полученных результатов. На рис. 9.1 приведен в качестве примера экспериментальный график тока в
цепи с последовательным соединением R, L, и C при двуполярном прямоугольном приложенном напряжении. На этот график наложены в том же масштабе два расчётных графика: один сделан с учётом только первой и третьей гармоник, а в другом учтены 5 гармоник – с первой по одиннадцатую.
В приложении приведена MathCAD-программа расчёта этих графиков с комментариями.
Экспериментальная часть
Задание
Рассчитать мгновенное и действующее значение тока и напряжения на конденсаторе, а также потребляемую цепью активную мощность при прямоугольном периодическом приложенном напряжении, построить график изменения тока на входе цепи, проверить результаты расчёта путём осциллографирования и непосредственных измерений.
Порядок выполнения работы
· Выбрать один из приведенных ниже вариантов параметров цепи (рис. 9.2) и выполнить расчёт согласно заданию, учитывая основную гармонику и одну – две высших. По результатам расчёта мгновенных значений на рис.9.3 построить графики, а действующие значения и мощность занести в табл. 9.1.
Варианты параметров элементов цепи и приложенного напряжения:
L = 10 мГн (RK=17 Ом), L = 40 мГн (RK=70 Ом), L = 100 мГн, (RK=170 Ом);
С = 0,22, 0,47 или 1 мкФ;
R = 47, 100, 150, или 220 Ом;
Um=8…10 B, f=0,5…1 кГц.
· Собрать цепь (рис.9.2) с принятыми в расчёте параметрами элементов, включить виртуальные приборы для измерения действующих значений тока и напряжения на конденсаторе и осциллограф.
· Установить на источнике принятые значение частоты и амплитуду прямоугольных импульсов и перенести осциллограмм на рис. 9.4. Записать в табл. 9.1 действующие значения тока и напряжения на конденсаторе.
· Переключить вольтметр на вход цепи, включить виртуальный измеритель активной мощности и занести его показание также в табл. 9.1.
· Сравнить результаты расчёта и эксперимента и сделать выводы.
Видео:Несимметричная нагрузка. Схема соединения "треугольник"Скачать

Треугольник короткого замыкания
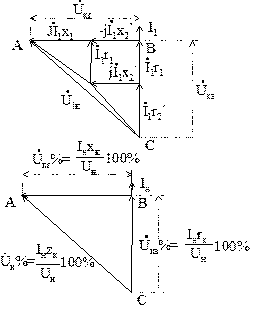
Используя схему замещения трансформатора при коротком замыкании, получим треугольник короткого замыкания. Из треугольника следует:
1)
2)
3)
Обычно треугольник короткого замыкания строится для номинального тока и стороны его выражены в процентах от номинального напряжения.
UK – представляет собой полное падение напряжения в обеих обмотках трансформатора.
Совмещение режимов
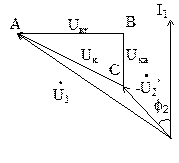
1) Путем наложения треугольника короткого замыкания на режим холостого хода получим режим нагрузки т.е. получим напряжение U ’ 2 и угол j2 между потоками I.
2) Потери при нагрузке равны потерям мощности при холостом ходе и коротком замыкании.
3) Ток нагрузки трансформатора равен току холостого хода и короткого замыкания.
Для холостого хода
Для короткого замыкания
а при нагрузке
4) Коэффициент полезного действия можно получить используя данные опыта холостого хода и короткого замыкания.
при холостом ходе P0 = PМГ
При коротком замыкании PК= PЭЛ1,2 = I 2 rк, 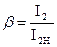
Тогда 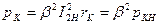
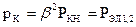
тогда
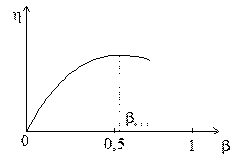
cosj2 = const построим зависимость h = f(b)
Максимум h наступает тогда, когда потери в стали равны потерям в меди.
| Uн Iн |
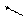
Относительное изменение напряжения — DU.
Изменением напряжения трансформатора называется (выраженная в % от номинального вторичного напряжения) арифметическая разность между номинальным вторичным напряжением при холостом ходе U2Н и напряжением U2 при номинальном токе.
1) при выводе используется предыдущая векторная диаграмма,
2) расчет проведем аналитически,
3) определим DU при номинальном токе,
4) примем U1 равным 100 ед. т.е. U1 = 100,
тогда 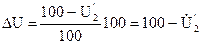
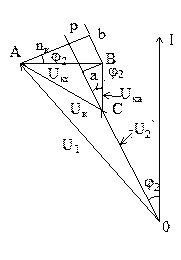
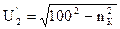
Принимаем первые два члена, т.к. начиная с третьего величина их мала
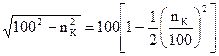
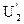
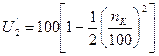
Выразим DU через составляющие напряжения короткого замыкания.
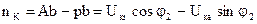
Величина второго члена очень мала и им можно пренебречь
тогда
Это выражение для b = 1, при различных значениях b
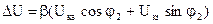
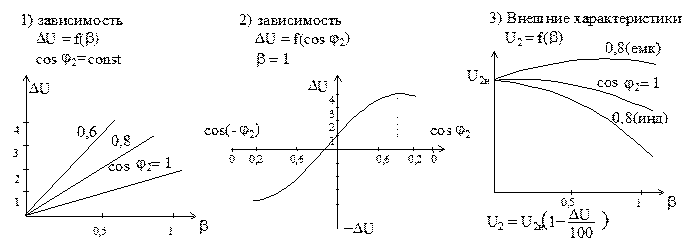
Видим, что, используя опыты холостого хода и короткого замыкания можно получить все характеристики трансформатора при нагрузке.
Видео:ЧТО ТАКОЕ КОРОТКОЕ ЗАМЫКАНИЕ [РадиолюбительTV 67]Скачать
![ЧТО ТАКОЕ КОРОТКОЕ ЗАМЫКАНИЕ [РадиолюбительTV 67]](https://i.ytimg.com/vi/EeZZAdAldrE/0.jpg)
Схемы соединений и особенности разомкнутого треугольника трансформатора напряжения
Автор: Евгений Живоглядов. Дата публикации: 17 июля 2013. Категория: Статьи.
Следует отличать соединение в разомкнутый треугольник (рисунок 1, а) от соединения в открытый треугольник (рисунок 1, б), называемого иногда V-образным. Рассмотрим на нескольких типичных примерах области их применения.
Рисунок 1. Различие между соединениями в разомкнутый (а) и открытый (б) треугольники. Примеры применения соединений в разомкнутый треугольник: утроитель частоты (в) и фильтр напряжения нулевой последовательности (г).
Видео:Этому не учат, а стоило бы. Чем отличается звезда от треугольника? #звезда #треугольник #двигательСкачать

Схемы соединений трансформаторов напряжения в открытый и разомкнутый треугольник
Схема соединения в открытый треугольник подразумевает, что оборудование подключено между сторонами двух фаз. При этом проводится электрический ток с внешней стороны, с вторичных обмоток числа пропорционально этому показателю. Реле и основная нагрузка пускаются между вторичной сетью, что позволяет получить нужный уровень сопротивления.
Данная схема позволяет подключить разу три источника. Обратить внимание следует на то, что подача организуется линейным способом, и нужно избегать прохождения тока от первого к третьему источнику и наоборот.
Разомкнутый же тип подключения применяются в выпрямительному оборудовании. При помощи соединения типа достигают тока тройной частоты, что при работе со звездой или открытым симметричным невозможно. Применяется вариант, когда три трансформатора с одной фазой подключаются к прибору, который увеличивает пропорционально три частоты работы.
При помощи рассматриваемой фигуры получают нулевую последовательность, то есть в нормальном функционале UP будет равно нулю.
Нейтраль первичной обмотки в обязательном порядке заземляется, а для вторичной выбирают параметры не менее чем в 100 Вольт, если заземление. Для изолированной коэффициент берется 100 к 3 В. Коэффициент троиться, следовательно, вторичные обмотки суммируют коэффициент трансформации также в три раза. Следовательно, для описанного выше примера он состоит 6 тысяч к ста к трем. Пик получается от трансформаторных обмоток внешней поверхности, так как подача ведется через вторичку. Обязательно заземление.
Обратно же возникает риск не для прибора, а для обслуживавшего его персонала. На производстве строго запрещено устанавливать защитную или коммутационную технику между приборами такого типа.
Видео:Направленная защита от замыканий на землюСкачать

Общие сведения
Трансформаторами напряжения, как правило, называют разновидность трансформаторов, которые предназначены не для передачи мощности, а для гальванического разделения высоковольтной стороны от низковольтной.
Такие трансформаторы предназначены для питания измерительных и управляющих приборов. На «высокой» стороне различных трансформаторов напряжения, естественно, напряжение может быть разным, это и 6000, и 35000 вольт и даже много более, а вот на «низкой» стороне (на вторичной обмотке) оно не превышает 100 вольт.
Это очень удобно для унификации приборов управления. Если делать измерительные приборы и приборы управления, а это в основном реле, на высокое напряжение, то они, во-первых, будут очень большими, а во-вторых, очень опасными в обслуживании.
Коэффициент трансформации указан на самом трансформаторе и может выглядеть как Кu = 6000/100, либо просто 35000/100. Разделив одно число на другое, получим в первом случае этот коэффициент 60, во втором 350.
Данные трансформаторы бывают как «сухие», в которых в качестве изоляции используется электрокартон. Они применяются, обычно, для напряжений до 1000 вольт. Пример НОС-0,5. Где, Н означает напряжение, имеется ввиду трансформатор напряжения, О – однофазный, С – сухой, 0,5 – 500 вольт (0,5кВ). А так же масляные: НТМИ, НОМ, 3НОМ, НТМК, в которых масло играет роль, как изолятора, так и охладителя. И литые, если быть точным, то с литой изоляцией (3НОЛ – трехобмоточный трансформатор напряжения однофазный с литой изоляцией), в которых все обмотки и магнитопровод залиты эпоксидной смолой.
Видео:Короткое замыкание! Электрик 150-го уровня!!!😄 Это было ожидаемо😉Скачать

Различие между соединениями
Основное отличие разомкнутого треугольника от открытого состоит в том, что при помощи него возможно получить напряжение нулевой последовательности. В случае же открытого подсоединения значения зажимов вторичек всегда пропорциональны междуфазному.
Но в любом случае для защиты трансформаторов с такой схемой используются автоматы и предохранители. Если происходит обрыв фазы, то происходит короткое замыкание.
Блокировка при помощи автоматов позволит избежать скачка, которое приводит к неисправностям обмотки. Контроль проводится с возможностью измерения.
Видео:Описание схемы переключения электродвигателя со звезды на треугольник.Скачать

Схема полной звезды ТТ
В схеме полной звезды (рис. 1, а) в реле проходят вторичные токи измерительных трансформаторов, поэтому коэффициент схемы kcx=1.
Защита может срабатывать при любом виде КЗ. Эта схема применяется обычно в сетях с глухозаземленной нейтралью, в которых могут возникать не только междуфазные, но и однофазные КЗ, сопровождающиеся протеканием тока в одной фазе. В сетях с изолированной (компенсированной) нейтралью (6-35 кВ) схема, как правило, не применяется, так как в этих сетях могут возникать лишь междуфазные КЗ, для фиксации которых достаточно иметь трансформаторы тока в двух фазах. Схема относительно дорогая, так как требует трех ТТ и трех реле тока.
Видео:Что такое НАПРЯЖЕНИЕ КОРОТКОГО ЗАМЫКАНИЯ ТРАНСФОРМАТОРАСкачать

В каких случаях применяют
Схематичное построение разомкнутого варианта для трансформатора применяется довольно часто на производстве. Дело в том, что благодаря ней можно использовать синхронизацию на силовых тс. Используется для соединения трансформаторов с одной фазой, если нет возможности установить трехфазный. Уберегает механизмы, в том числе и электрические двигатели от подачи на два, если нет напряжения в одной из фаз. Единственно допустимой схемой сборки является в случае, если ротор установлен в расточку статора.
Видео:Короткое замыканиеСкачать

Особенности схем подключения нагрузок к тиристорному регулятору
Наиболее часто на практике используется четыре схемы подключения нагрузок к тиристорному регулятору: звезда, треугольник, звезда с рабочей нейтралью и разомкнутый треугольник.
Схемы подключения звезда и треугольник приведены на рисунке 1.
Рисунок 1 Подключение нагрузки к трехфазному тиристорному регулятору по схемам звезда и треугольник
Основное достоинство этих двух схем – простота и минимальное количество силового провода, за счет чего они и получили наиболее широкое распространение. При соединении нагрузки звездой максимальное напряжение на нагрузочном сопротивлении равно фазному напряжению Uф, а при соединении треугольником – линейному Uл. Соответственно, звездой соединяют нагрузку, рассчитанную на напряжение 220 В, а треугольником – 380 В.
Кривая тока, протекающего по фазному проводу изображена на рисунке 2.
Рисунок 2 Кривая тока в фазах при соединении звездой или треугольником, активная нагрузка
Однако у простоты схемы есть обратная сторона медали – напряжения на нагрузочных сопротивлениях распределяются поровну только при условии строго равенства фазных напряжения (Uа = Ub = Uс) и равенства сопротивлений нагрузок (Ra = Rb = Rc или Rab = Rbc = Rca). Как правило, на практике это условие почти никогда не выполняется и возникает небаланс напряжений: на разных сопротивления нагрузки при полностью включенных тиристорах устанавливаются неравные напряжения, например, на одном сопротивлении 210 В, на другом 215 В, на третьем 230 В.
В большинстве своем эти небалансы невелики: разброс по напряжению невелик и составляет не больше 4-8%, что вполне допустимо. Но иногда при неудачном соотношении параметров – сильном «перекосе» фаз с одновременно неравными сопротивлениями нагрузки — напряжения могут распределиться с большим разбросом, например 190, 220 и 250 В. Это ведет к неравномерному износу ТЭНов и преждевременному выгоранию одного из них.
Довольно часто бывает, что в одной из фаз постоянно выгорает ТЭН неизвестно от чего. Обычно это является следствием выше описанного явления.
В схемах подключения звезда с рабочей нейтралью и разомкнутый треугольник (рисунок 3) это явление проявляется гораздо меньшей степени.
Рисунок 3 Подключение нагрузок по схемам звезда с рабочей нейтралью и разомкнутый треугольник
При подключении нагрузки по схеме звезда с нулем максимальное напряжение на нагрузочном сопротивлении равно фазному напряжению сети, при этом ток каждой фазы определяется лишь напряжением фазы и сопротивлением нагрузочного резистора, включенного в эту фазу, и не зависит напряжений других фаз и от сопротивлений остальных нагрузочных сопротивлений, то есть Ia = Ua / Ra, Ib = Ub / Rb, Ic = Uc / Rc.
Другое важное свойство схемы – возможность выравнивания токов, напряжений и мощностей на нагрузочных сопротивлениях в случае «перекоса» фаз питающей сети. Например, тиристорный регулятор ТРМ-С может автоматически корректировать напряжение на нагрузке таким образом, чтобы на каждом сопротивлении нагрузки выделялась равная мощность. Это способствует продлению срока службы ТЭНов, а также энергосбережению – за счет устранения перекосов по фазам достигается дополнительная экономия электроэнергии 1-3%.
Еще один плюс этой схемы – это меньший уровень излучаемых электромагнитных помех.
Все выше сказанное также верно и для схемы разомкнутого треугольника, с той лишь разницей, что максимальное напряжение на нагрузочных сопротивлениях равно линейному, а ток нагрузки определяется линейным напряжением Iab = Uab / Rab, Ibc = Ubc / Rbc, Ica = Uca / Rca.
Недостатков у схемы звезда с нейтралью два. Первый – это необходимость подключения нулевого провода, что на практике иногда бывает затруднительно. Например, у нагревательного аппарата может быть сделано три вывода для подключения фазных проводов, а общая точка звезды – внутри аппарата и недоступна для подключения. В этом случае реализовать подключение по схемы звезды с нейтралью невозможно.
Второй недостаток – это протекание тока через нейтраль при фазо-импульсном управлении даже при полностью равных сопротивлениях нагрузки и фазных напряжениях, что проиллюстрировано на рисунке 4: в верхней его части изображены кривые токов, протекающие по фазам А, В и С, а внизу – ток в нулевом проводе.
Рисунок 4 Протекание тока через нулевой проводник
При этом величина тока в нулевом проводе может быть в 1,5-2 раза больше чем ток в фазах. Это приводит к необходимости прокладки нулевого проводника увеличенным сечением, что, разумеется, увеличивает и стоимость кабельных линий. Незнание или недооценка же этого явления приводит к постепенному выходу из строя нейтрального провода.
Это иногда вызывает удивление: казалось бы, напряжения фаз равные, сопротивления фаз равные, откуда ток в нуле?! Но объясняется это явление просто. Дело в том, что при фазо-импульсном управлении тиристорами форма тока становится не синусоидальной и поэтому не происходит полной компенсации токов в нулевом проводе, как при питании трехфазной нагрузки синусоидальным током.
Отсюда вывод – чтобы ток в нулевом проводе был минимальный необходимо использовать управление пропуском периодов. В этом случае токи фаз будут синусоидальны, а значит ток в нейтрали будет определятся лишь небалансом напряжений фаз и сопротивлений. Практически, это приводит к тому, что ток в нуле становится не больше 10% от тока фазы.
Напоследок, рассмотрим схему соединения разомкнутый треугольник. У схемы есть замечательное свойство – тиристоры при таком соединении коммутируют не фазные токи, а линейные, которые меньше в 1,73 раза. Например, если ток фазы составляет 650 А, то токи в линейных проводах составляют Iл = 650 / 1,73 = 380 А. По сравнению со схемой соединения обычным треугольником, это дает возможность приобретать тиристорный регулятор на меньший номинальный ток, который соответственно дешевле и меньше в габаритах. Это показано на рисунке 5. В верхней части рисунка нагрузка соединена треугольником, при этом через тиристоры протекают токи 650 А, а значит необходимо приобретение тиристорного регулятора номинальным током не менее 700-800 А. А в нижней части нагрузка соединена разомкнутым треугольником, при этом по фазам протекает такой же ток 650 А, но поскольку тиристоры коммутируют ток 380 А, то достаточно иметь тиристорный регулятор с номинальным током 400-500 А, что в 1,5-2 раза дешевле.
Рисунок 5 Сравнение схем треугольник и разомкнутый треугольник
Жаль, но несмотря на такое преимущество, эта схема не получила большого распространения. Почему? Первое, как и для звезды с нейтралью, для реализации такой схемы подключения должны быть доступны оба конца выводов нагрузок, что опять же не всегда возможно. Например, у трансформатора, первичная обмотка которого соединена треугольником чаще всего выведена только три конца, а вторые три спрятаны внутри. Второе – это увеличенная стоимость кабельного хозяйства – посмотрите внимательно на рисунок 5: при соединении разомкнутым треугольником требуется дополнительный силовой кабель ( «обратный» кабель от нагрузки). Учитывая высокую стоимость кабелей, можно сказать, что такая схема целессобразно лишь при небольшой длине кабельных линий до 20-30 метров при прокладке медным кабелем и до 50-70 метров при прокладке алюминиевым. При большой длине экономия, полученная от приобретения более дешевого регулятора обнуляется за счет более высокой стоимости кабельного хозяйства.
Видео:Короткое замыкание 6 кВСкачать

Схема неполной звезды ТТ с реле в обратном проводе
В схеме неполной звезды с реле в обратном проводе (рис. 1, в) через реле 3КА, включенное в обратный провод, проходит сумма вторичных токов фаз А и С или (при междуфазных КЗ) ток фазы В с обратным знаком [Л1, с.42]:
Схема обладает достоинством схемы неполной звезды (использование двух ТТ) и имеет такую же чувствительность при двухфазных КЗ за трансформатором У/Д-11, как и схема полной звезды. Коэффициент схемы kcx = 1.
Схема неполной звезды с реле в обратном проводе или без него нашла широкое распространение в токовых защитах линий напряжением до 35 кВ включительно (т.е. в сетях с изолированной нейтралью).
💥 Видео
Котика ударило током, 10 т. ВольтСкачать

Все про короткое замыканиеСкачать
Трехфазные цепи │Аварийный режим - короткое замыкание фазы С │задачаСкачать

Часть 1. Замыкание на землю в сети с изолированной нейтралью.Скачать
Расчёт токов короткого замыкания для курсового проекта Электроснабжение предприятий разделы 4.1-4.2Скачать

Короткое замыкание за трансформатором D/Y-nСкачать

Короткое замыкание. Защита от короткого замыканияСкачать

09 Расчёт токов короткого замыкания - Электроснабжение населённого пунктаСкачать

Ударный ток короткого замыканияСкачать

Фильтрация токов НП через “треугольник” ТТСкачать

#001."Звезда" или "Треугольник"?Скачать





















 Аварийные режимы в нагрузках соединенных треугольником
Аварийные режимы в нагрузках соединенных треугольником