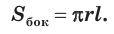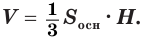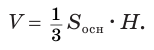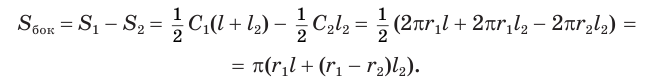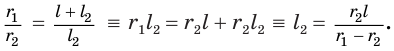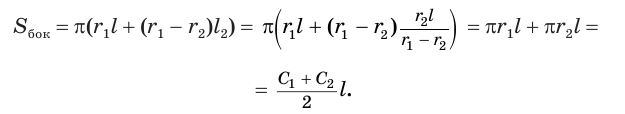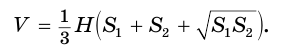Так как все образующие конуса равны, то его осевым сечением является равнобедренный треугольник, боковыми сторонами которого являются образующие конуса, а основанием — диаметр конуса. При этом все осевые сечения конуса — равные равнобедренные треугольники . На рисунке 168 осевым сечением конуса является треугольник ABP ( АР = ВР ). Угол АPВ называют углом при вершине осевого сечения конуса .
Конус, в осевом сечении которого правильный треугольник, называется равносторонним конусом.
Если секущая плоскость проходит через вершину конуса, пересекает конус, но не проходит через его ось, то в сечении конуса также получается равнобедренный треугольник (см. рис. 168: △ DCP ).
Так как конус — тело вращения, то любое сечение конуса плоскостью, перпендикулярной его оси (т. е. параллельной основанию конуса), есть круг, а сечение боковой поверхности конуса такой плоскостью — окружность этого круга; центром круга (окружности) является точка пересечения оси конуса и секущей плоскости (рис. 169).
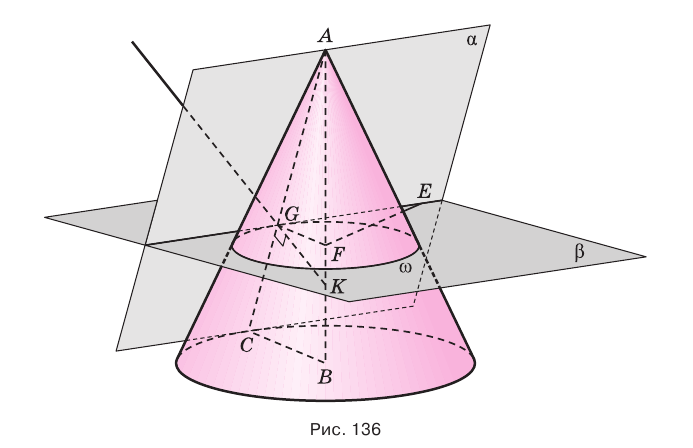
Если секущая плоскость не параллельна плоскости основания конуса и не пересекает основание, то сечением боковой поверхности конуса такой плоскостью является эллипс (рис. 170). Поэтому эллипс называют коническим сечением .

О конических сечениях можно прочитать в очерках «Элементарная геометрия», «Проективная геометрия» в конце этой книги.
ЗАДАЧА (3.047). Высота конуса равна радиусу R его основания. Через вершину конуса проведена плоскость, отсекающая от окружности основания дугу: а) в 60 ° ; б) в 90 ° . Найти площадь сечения.
Решени е. Рассмотрим случай а). Пусть плоскость α пересекает поверхность конуса с вершиной Р по образующим РА и РВ (рис. 172); △ АВР — искомое сечение. Найдём площадь этого сечения.
Хорда АВ окружности основания стягивает дугу в 60 ° , значит, △ AOB — правильный и АВ = R .
Если точка С — середина стороны АB, то отрезок PC — высота треугольника АВР. Поэтому S △ ABP = 



Тогда S △ ABP = 

Ответ: а) 
18.3. Касательная плоскость к конусу
Определение. Касательной плоскостью к конусу называется плоскость, проходящая через образующую конуса перпендикулярно осевому сечению, проведённому через эту образующую.
Говорят, что плоскость α касается конуса по образующей РА (рис. 173): каждая точка образующей РА является точкой касания плоскости α и данного конуса.
Через любую точку боковой поверхности конуса проходит только одна его образующая. Через эту образующую можно провести только одно осевое сечение и только одну плоскость, перпендикулярную плоскости этого осевого сечения. Следовательно, через каждую точку боковой поверхности конуса можно провести лишь одну плоскость, касательную к данному конусу в этой точке.
18.4. Изображение конуса
Для изображения конуса достаточно построить: 1) эллипс, изображающий окружность основания конуса (рис. 174); 2) центр О этого эллипса; 3) отрезок ОР, изображающий высоту конуса; 4) касательные прямые РА и PB из точки Р к эллипсу (их проводят с помощью линейки на глаз).
Для достижения наглядности изображения невидимые линии изображают штрихами.
Необходимо заметить, что отрезок АВ, соединяющий точки касания образующих и окружности основания конуса, ни в коем случае не является диаметром основания конуса, т. е. этот отрезок не содержит центра О эллипса. Следовательно, △ АBP — не осевое сечение конуса. Осевым сечением конуса является △ ACP, где отрезок AC проходит через точку О, но образующая PC не является касательной к окружности основания.
18.5. Развёртка и площадь поверхности конуса
Пусть l — длина образующей, R — радиус основания конуса с вершиной Р .
Поверхность конуса состоит из боковой поверхности конуса и его основания. Если эту поверхность разрезать по одной из образующих, например по образующей PA (рис. 175), и по окружности основания, затем боковую поверхность конуса развернуть на плоскости (рис. 176, a ), то получим развёртку поверхности конуса (рис. 176, б ), состоящую из: а) кругового сектора, радиус которого равен образующей l конуса, а длина дуги сектора равна длине окружности основания конуса; б) круга, радиус которого равен радиусу R основания конуса. Угол сектора развёртки боковой поверхности конуса называют углом развёртки конуса ; его численная величина равна отношению длины окружности основания конуса к его образующей (радиусу сектора развёртки):
α = 
За площадь боковой поверхности конуса принимается площадь её развёртки. Выразим площадь боковой поверхности конуса через длину l его образующей и радиус R основания.
Площадь боковой поверхности — площадь кругового сектора радиуса длины l — вычисляется по формуле
S бок = 
где α — величина угла (в радианах) сектора — развёртки. Учитывая, что α = 
Таким образом, доказана следующая теорема.
Теорема 27. Площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую. ▼
Площадь полной поверхности конуса равна сумме площадей его боковой поверхности и основания, т. е.
S кон = π Rl + π R 2 . (3)
Следствие. Пусть конус образован вращением пря м оугольного треугольника ABC вокруг катета АС (рис. 177). Тогда S бок = π • BC • АВ. Если D — середина отрезка АВ, то AB = 2 AD, поэтому
S бок = 2 π ВС • AD. (4)
Проведём DE ⟂ АB ( E ∈ l = AС ) . Из подобия прямоугольных треугольников ADE и ACB (у них общий угол А ) имеем


Тогда соотношение (4) принимает вид
S бок = (2 π • DE ) • AC, (6)
т. е. площадь боковой поверхности конуса равна произведению высоты конуса на длину окружности, радиус которой равен длине серединного перпендикуляра, проведённого из точки на оси конуса к его образующей.
Это следствие будет использовано в п. 19.7.
18.6. Свойства параллельных сечений конуса

Теоремa 28. Если конус пересечён плоскостью, параллельной основанию, то: 1) все образующие и высота конуса делятся этой плоскостью на пропорциональные части; 2) в сечении получается круг; 3) площади сечения и основания относятся, как квадраты их расстояний от вершины.
Доказательств о. 1) Пусть конус с вершиной Р и основанием F пересечён плоскостью α , параллельной плоскости β основания конуса и расположенной между Р и β (рис. 178).
Проведём высоту РО конуса, где точка О — центр круга F. Так как РО ⟂ β , α || β , то α ⟂ РО. Значит, в сечении конуса плоскостью α получается круг с центром в точке O 1 = α ∩ РО. Обозначим этот круг F 1 .
Рассмотрим гомотетию 
Так как при гомотетии её центр является неподвижной точкой, прямая, проходящая через центр гомотетии, отображается на себя, а пересечение двух фигур — на пересечение их образов, то гомотетия 



где k — коэффициент гомотетии 
А поскольку гомотетия является подобием, то круг F 1 , являющийся параллельным сечением конуса, подобен его основанию.
Вследствие того что отношение площадей гомотетичных фигур равно квадрату коэффициента гомотетии и k = PO 1 : Р О , где РO 1 и PO — расстояния соответственно параллельного сечения и основания пирамиды от её вершины, то
S сечен : S основ = k 2 = 
18.7. Вписанные в конус и описанные около конуса пирамиды
Определение. Пирамида называется вписанной в конус, если у них вершина общая, а основание пирамиды вписано в основание конуса. В этом случае конус называется описанным около пирамиды.
Для построения изображения правильной пирамиды, вписанной в конус:
— строят изображение основания пирамиды — правильного многоугольника, вписанного в основание конуса;
— соединяют отрезками прямых вершину конуса с вершинами построенного многоугольника;
— выделяют видимые и невидимые (штрихами) линии изображаемых фигур.
На рисунках 179—182 изображена вписанная в конус пирамида, в основаниях которой лежит:
— прямоугольный треугольник (см. рис. 179);
Видео:№550. Осевое сечение конуса — прямоугольный треугольник. Найдите площадь этого сечения, еслиСкачать

Конус в геометрии — элементы, формулы, свойства с примерами
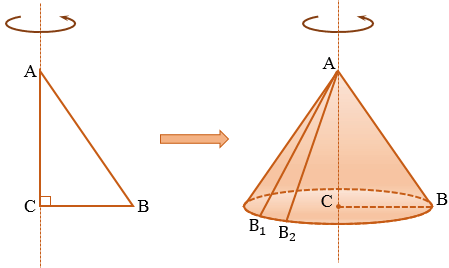
Конусом называется тело, полученное вращением прямоугольного треугольника вокруг оси, проходящей через один из его катетов (рис. 126).
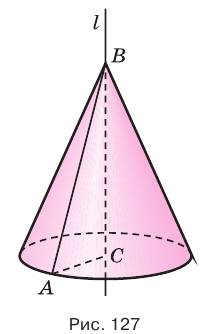
На рисунке 127 показано образование конуса при вращении прямоугольного треугольника 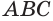
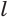
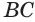
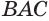
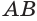
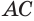
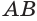
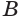
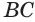
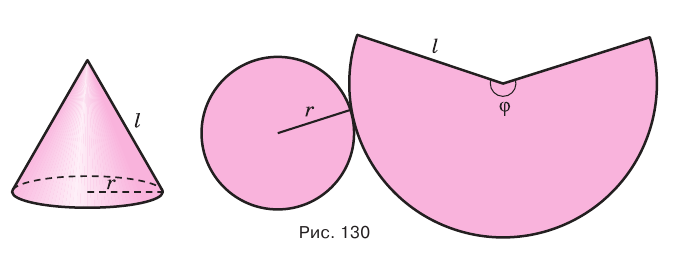
Поверхность конуса можно развернуть на плоскость, в результате получится сектор, представляющий боковую поверхность конуса, и круг, представляющий основание конуса. На рисунке 130 представлены конус и его развертка.
Теорема 5.
Боковая поверхность конуса равна произведению полуокружности его основания и образующей:
Доказательство проведите самостоятельно, используя рисунок 130.
Важной пространственной конфигурацией, которая часто встречается в задачах, является сочетание конуса с плоскостью.
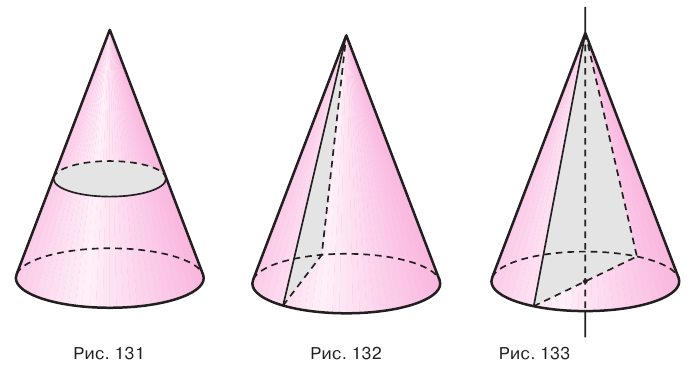
Если конус пересечь плоскостью, параллельной основанию, то получится круг (рис. 131), а если плоскостью, проходящей через вершину, то — равнобедренный треугольник, у которого боковые стороны являются образующими конуса (рис. 132).
Осевое сечение конуса, т. е. сечение плоскостью, проходящей через ось конуса, является равнобедренным треугольником, у которого основание равно диаметру основания конуса (рис. 133).
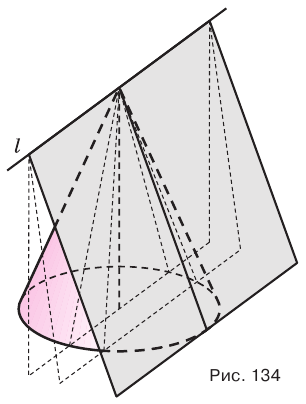
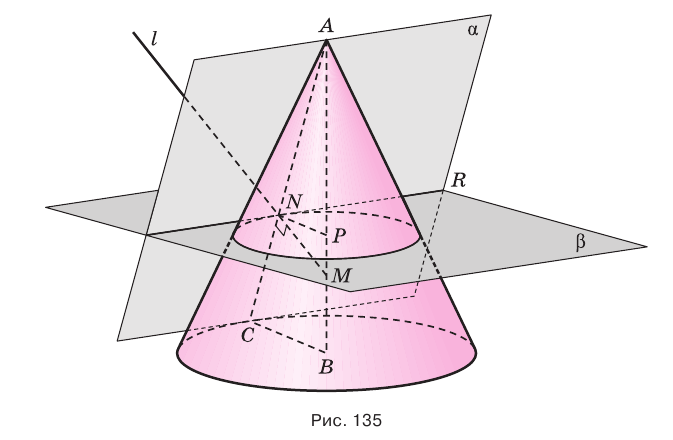
Проведем через вершину конуса секущую плоскость и будем ее поворачивать вокруг прямой, перпендикулярной оси конуса (рис. 134). При этом основание треугольника-сечения будет укорачиваться, а его боковые стороны сближаться до того момента, пока не совпадут. Получим плоскость, целиком содержащую образующую и не имеющую с конусом других общих точек. Такая плоскость называется касательной плоскостью конуса.
Теорема 6.
Если плоскость касается конуса по некоторой образующей, то ей перпендикулярна плоскость, проходящая через эту образующую и ось конуса.
Доказательство:
Пусть плоскость 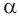

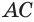

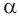
Проведем прямую 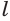

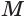
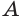
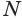
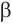

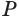
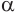
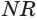
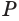
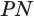
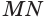
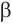
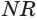
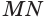
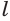
Таким образом, прямая 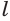

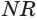
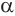
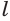

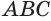
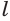

Теорема 6 выражает свойство касательной плоскости конуса.
Теорема 7.
Плоскость касается конуса, если она проходит через его образующую и перпендикулярна плоскости, проходящей через эту образующую и ось конуса.
Доказательство:
Пусть плоскость 


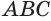



Точки образующей 

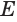


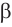

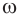
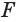

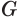

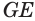
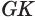


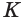
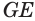
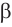
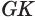
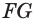
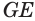
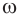
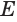
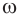
Теорема 7 выражает признак касательной плоскости конуса.
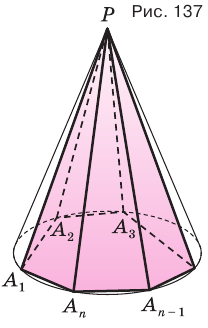
Пусть есть конус с вершиной 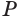
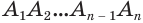
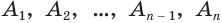
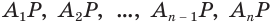
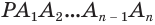
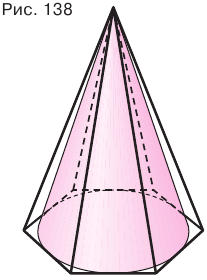
Если основание конуса вписано в основание пирамиды, а боковая поверхность конуса касается боковых граней пирамиды, то говорят, что пирамида описана около конуса, или конус вписан в пирамиду (рис. 138).
Теорема 8.
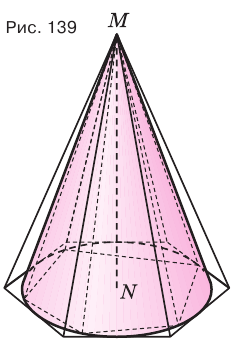
Объем конуса равен третьей доле произведения площади Рис. 139 т его основания и высоты:
Доказательство:
Пусть есть конус с осью 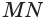
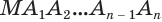
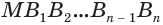
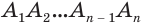
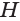
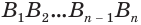
Будем увеличивать количество 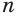
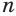
В описанном процессе высота 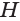
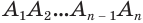
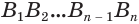
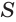
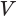
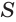
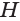
Теорема 9.
Если конус пересечь плоскостью, параллельной его основанию, то:
- а) образующая и высота разделяются на пропорциональные части;
- б) площади сечения и основания относятся как квадраты их расстояний от вершины.
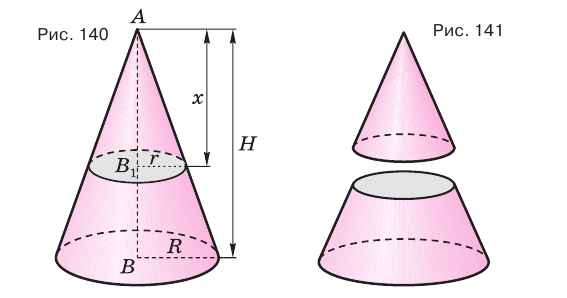
Используя рисунок 140, докажите эту теорему самостоятельно.
Секущая плоскость, параллельная основанию конуса, разделяет его на две части (рис. 141). Одна из этих частей также является конусом, а другая — телом, которое называется усеченным конусом.
Основание данного конуса и круг, полученный в сечении, называют основаниями усеченного конуса, а отрезок образующей данного конуса, заключенный между его основанием и секущей плоскостью, — образующей усеченного конуса (рис. 142). Высотой усеченного конуса называется перпендикуляр, проведенный из какой-либо точки одного его основания к плоскости другого основания.
Усеченный конус можно получить вращением прямоугольной трапеции вокруг боковой стороны, к которой прилежат прямые углы (рис. 143).
Пример:
Найдем боковую поверхность усеченного конуса. Пусть есть усеченный конус, у которого радиусы оснований 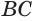
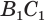
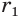
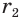
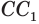
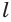
Достроим его до полного конуса. Достроенная часть представляет собой конус, у которого радиус основания равен 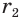
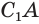
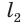
Боковую поверхность 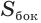
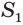
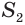
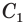
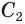
Найдем 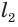
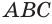
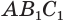
Таким образом, боковая поверхность усеченного конуса равна произведению полусуммы длин окружностей его оснований и образующей.
Пример:
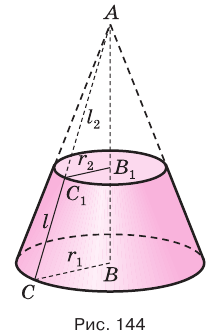
Используя рисунок 144, можно, как и для усеченной пирамиды (см. параграф 9), доказать, что объем 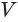
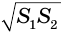
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Сфера в геометрии
- Шар в геометрии
- Правильные многогранники в геометрии
- Многогранники
- Возникновение геометрии
- Призма в геометрии
- Цилиндр в геометрии
- Пирамида в геометрии
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:№551. Осевое сечение конуса — правильный треугольник со стороной 2г. Найдите площадь сечения,Скачать

Конус
Конус — это объемное тело, которое получается при вращении прямоугольного треугольника вокруг одного из его катетов.
Возьмем прямоугольный треугольник АВС. Будем вращать этот треугольник вокруг катета АС.
Прямая АС — ось косинуса.
Отрезок АС — высота конуса.
Основание конуса — круг, образованный при вращении катета ВС.
Коническая поверхность (или боковая поверхность конуса) — поверхность, образованная при вращении гипотенузы АВ и состоящая из отрезков с общим концом А.
Образующие конуса — отрезки, из которых составлена боковая поверхность конуса (на рисунке выше указаны образующие АВ, АВ1 и АВ2).
Определение
| Конус — это тело, ограниченное кругом и конической поверхностью. |
Объем конуса
| Объем конуса равен одной трети произведения площади основания на высоту. |
Доказательство
Дано: конус с площадью основания S, высотой h и объемом V.
Доказать: V = 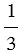
Доказательство:
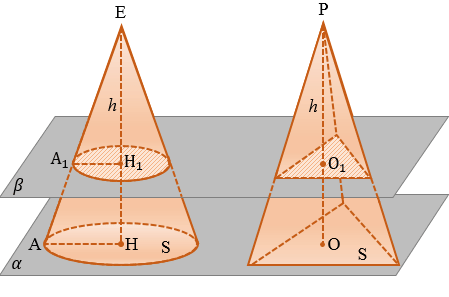
Воспользуемся принципом Кавальери. Рассмотрим конус и пирамиду с площадями оснований S и высотами ЕН = h и РО = h соответственно, «стоящие» на одной плоскости 
Проведем секущую плоскость 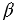

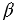
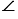

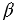
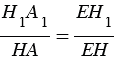
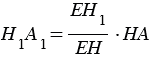
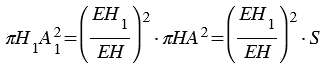
Площадь сечения пирамиды равна 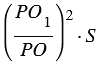
Следовательно, площадь сечения конуса равна площади сечения пирамиды. Поэтому и его объем равен объему пирамиды, т.е. V = 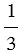
Площадь боковой поверхности конуса
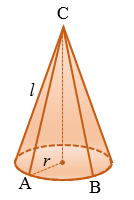
Рассмотрим конус с радиусом основания 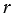
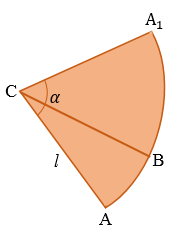
Представим, что его боковую поверхность разрезали по одной из образующих и развернули так, что получился круговой сектор.
Радиус этого сектора равен образующей конуса, т.е. равен 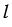
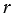

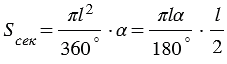
Длина дуги окружности с градусной мерой 
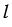
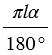
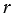
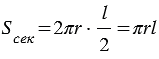
Площадь боковой поверхности конуса равна площади ее развертки, т.е. 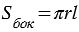 . . |
Поделись с друзьями в социальных сетях:
🎦 Видео
Геометрия 11 класс (Урок№7 - Конус.)Скачать

Стереометрия | КонусСкачать

Задание 42. УСЕЧЕННЫЙ КОНУС. Часть 1Скачать

Простой расчёт развёртки конусаСкачать

ГЕОМЕТРИЯ 11 класс: Конус Площадь конуса. Усеченный конусСкачать

Конус. 11 класс.Скачать

Понятие конуса. Видеоурок по геометрии 11 классСкачать

Сечение конусаСкачать

Конус. Практическая часть. 11 класс.Скачать

Решение задач на конусСкачать

Как начертить КОНУС С ВЫРЕЗОМ (чертеж + аксонометрия)Скачать

Конус путем вращения треугольникаСкачать

Часть 2. ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ. Блок 10. Конус. Урок 3. Сечение плоскостью под углом к основанию.Скачать
сечение конусаСкачать

2 3 проекция точки на конусеСкачать

Конус. Урок 8. Геометрия 11 классСкачать

Построение линии пересечения поверхности конуса с проецирующей плоскостьюСкачать

Усеченный конус. Практическая часть. 11 класс.Скачать