Контур треугольника с вершинами (7 видео)

Интеграл по замкнутому контуру, формула Грина, примеры

Если дан криволинейный интеграл, а кривая, по которой происходит интегрирование — замкнутая (называется контуром), то такой интеграл называется интегралом по замкнутому контуру и обозначается следующим образом:

Область, ограниченную контуром L обозначим D. Если функции P(x, y) , Q(x, y) и их частные производные и — функции, непрерывные в области D, то для вычисления криволинейного интеграла можно воспользоваться формулой Грина:

Таким образом, вычисление криволинейного интеграла по замкнутому контуру сводится к вычислению двойного интеграла по области D.

Формула Грина остаётся справедливой для всякой замкнутой области, которую можно проведением дополнительных линий на конечное число простых замкнутых областей.

Пример 1. Вычислить криволинейный интеграл

если L — контур треугольника OAB , где О(0; 0) , A(1; 2) и B(1; 0) . Направление обхода контура — против часовой стрелки. Задачу решить двумя способами: а) вычислить криволинейные интегралы по каждой стороне треугольника и сложить результаты; б) по формуле Грина.

а) Вычислим криволинейные интегралы по каждой стороне треугольника. Сторона OB находится на оси Ox , поэтому её уравнением будет y = 0 . Поэтому dy = 0 и можем вычислить криволинейный интеграл по стороне OB :

Уравнением стороны BA будет x = 1 . Поэтому dx = 0 . Вычисляем криволинейный интеграл по стороне BA :

Уравнение стороны AO составим, пользуясь формулой уравнения прямой, проходящей через две точки:

Таким образом, dy = 2dx . Вычисляем криволинейный интеграл по стороне AO :

Данный криволинейный интеграл будет равен сумме интегралов по краям треугольника:

б) Применим формулу Грина. Так как , , то . У нас есть всё для того, чтобы вычислить данный интеграл по замкнутому контуру по формуле Грина:

Как видим, получили один и тот же результат, но по формуле Грина вычисление интеграла по замкнутому контуру происходит значительно быстрее.

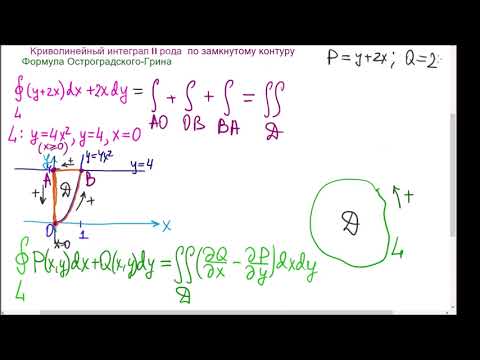
Пример 2. Пользуясь формулой Грина, вычислить криволинейный интеграл

где L — контур OAB , OB — дуга параболы y = x² , от точки О(0; 0) до точки A(1; 1) , AB и BO — отрезки прямых, B(0; 1) .

Решение. Так как функции , , а их частные производные , , D — область, ограниченная контуром L , у нас есть всё, чтобы воспользоваться формулой Грина и вычислить данный интеграл по замкнутому контуру:

Пример 3. Пользуясь формулой Грина, вычислить криволинейный интеграл

, если L — контур, который образуют линия y = 2 − |x| и ось Oy .

Решение. Линия y = 2 − |x| состоит из двух лучей: y = 2 − x , если x ≥ 0 и y = 2 + x , если x .

Имеем функции , и их частные производные и . Подставляем всё в формулу Грина и получаем результат:

Пример 4. С помощью формулы Грина вычислить криволинейный интеграл

если L — окружность .

Решение. Функции , и их частные производные и непрерывны в замкнутом круге . Подставляем всё в формулу Грина и вычисляем данный интеграл:

Содержание

Контур треугольника с вершинами
Контакты
—>Решение задач и примеров —>
🔍 Видео

Видео:Криволинейный интеграл 1-го рода ★ Криволинейный интеграл по длине дуги ★ ∫(x+y)dsСкачать

Контур треугольника с вершинами

Учасники групи мають 10% знижку при замовленні робіт, і ще багато бонусів!

Контакты

Администратор, решение задач
Роман

Tel. +380685083397
[email protected]
skype, facebook:
roman.yukhym

Решение задач
Андрей

facebook:
dniprovets25

Видео:Формула Остроградского - ГринаСкачать

—>Решение задач и примеров —>

—>

Вычисление двойных, тройных интегралов [18]

Приложения двойных интегралов [7]

Приложения тройных интегралов [4]

Вычисление криволинейных интегралов [7]

Элементы теории поля [9]

—>

—> 23.08.2021
ЮMoney+Банковская карта. Принимаются виды оплат: MasterCard, Visa, МИР, ЮMoney-кошелек (Снижена комиссия)
Оплата картой Каспи для Казахстана, пишите на почтовый ящик pmaxim2006@mail.ru

23.08.2021
В Digiseller можно найти все решения, что и на fizmathim.ru Перейти в Магазин на Digiseller
Можно воспользоваться формой поиска по первым 3-4 словам. Способы оплаты: Банковская карта (РФ, СНГ)(Visa/MasterCard/Мир), QIWI, Webmoney, Скины Steam
Digiseller удобен для студентов из стран СНГ

26.04.2019
— Все задачи оформлены в текстовом редакторе Microsoft Word, по просьбе в индивидуальном порядке могу выслать в PDF формате.

— Ссылки действительны в течение 24 часов до первой попытки скачать (90 минут с момента первого скачивания).

05.02.2019
— При добавлении товаров в корзину на сумму выше 250 руб. и оформлении заказа активируется 5 % скидка на оплату.

— Ссылка на скачивание задач, приходит на указанный вами почтовый ящик при оформлении заказа и его оплаты. Дополнительная рассылка оплаченных заказов на E-mail производится в течение нескольких минут/часов, тема писем имеет вид «Заказ xxxxx». —>