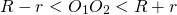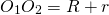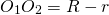Концентрические окружности пересекающиеся окружности (2 видео)

Геометрия. 9 класс

Две окружности могут пересекаться, не пересекаться либо касаться друг друга.
Перейдем к анализу возможных случаев расположения двух окружностей.
Рассмотрим окружность с центром О₁ и окружность с центром О₂. Тогда расстояние между их центрами равно О₁О₂.
I. Пересекающиеся окружности имеют две общие точки.
Расстояние между центрами двух пересекающихся окружностей больше разности, но меньше суммы их радиусов:
II. Не пересекающиеся окружности не имеет общих точек.

Если одна окружность лежит внутри другой, то расстояние между центрами меньше разности их радиусов:
Если одна окружность находится вне другой, расстояние между центрами больше суммы их радиусов:
III. Касающиеся окружности имеют одну общую точку – точку касания.
При внешнем касании расстояние между центрами окружностей равно сумме их радиусов:
При внутреннем касании расстояние между центрами равно разности радиусов:
Если центры окружностей совпадают, то такие окружности называются концентрическими.
Концентрические окружности разного радиуса не пересекаются: О₁О₂ = 0
В случае равенства радиусов они совпадают.
Если же радиусы этих окружностей не равны, то одна из них лежит внутри другой – образуется кольцо.

Кольцом называют фигуру, заключенную между концентрическими окружностями.

Содержание

НАШИ ПАРТНЁРЫ
Взаимное расположение окружностей
Окружность. Относительное взаимоположение окружностей.
🔍 Видео

Видео:Планиметрия 12 | mathus.ru | расстояние между центрами пересекающихся окружностейСкачать

НАШИ ПАРТНЁРЫ

Видео:Метод эксцентрических сферСкачать

Взаимное расположение окружностей

Выясним, каким может быть взаимное расположение двух окружностей.

Две окружности могут пересекаться, не пересекаться либо касаться друг друга.

I. Пересекающиеся окружности имеют две общие точки.

Расстояние между центрами двух пересекающихся окружностей больше разности, но меньше суммы их радиусов:

II. Не пересекающиеся окружности не имеет общих точек.

Если одна окружность лежит внутри другой, то расстояние между центрами меньше разности их радиусов:

Если одна окружность находится вне другой, расстояние между центрами больше суммы их радиусов:

R + r]» title=»Rendered by QuickLaTeX.com»/>

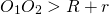
III. Касающиеся окружности имеют одну общую точку — точку касания.

При внешнем касании расстояние между центрами окружностей равно сумме их радиусов:

При внутреннем касании расстояние между центрами равно разности радиусов:

Концентрические окружности разного радиуса не пересекаются. Расстояние между центрами концентрических окружностей равно нулю: O1O2=0.

Видео:Задача №16. Пересекающиеся и касающиеся окружности.Скачать

Окружность. Относительное взаимоположение окружностей.

Если две окружности имеют только одну общую точку, то говорят, что они касаются.

Если же две окружности имеют две общие точки, то говорят, что они пересекаются.

Трех общих точек две не сливающиеся окружности иметь не могут, потому, что в противном случае через три точки можно было бы провести две различные окружности, что невозможно.

Будем называть линией центров прямую, проходящую через центры двух окружностей (например, прямую OO₁).

Теорема.

Если две окружности имеют общую точку по одну сторону от линии центров, то они имеют общую точку и по другую сторону от этой линии, т.е. такие окружности пересекаются.

Пусть окружности O и O₁ имеют общую точку A, лежащую вне линии центров OO_1. Требуется доказать, что эти окружности имеют еще общую точку по другую сторону от прямой OO₁.

Опустим из A на прямую OO₁ перпендикуляр AB и продолжим его на расстояние BA₁, равное AB. Докажем теперь, что точка A₁ принадлежит обеим окружностям. Из построения видно, что точки O и O₁ лежат на перпендикуляре, проведенном к отрезку AA₁ через его середину. Из этого следует, что точка O одинаково удалена от A и A₁. То же можно сказать и о точке O₁. Значит обе окружности, при продолжении их, пройдут через A₁.Таким образом, окружности имеют две общие точки : A (по условию) и A₁ (по доказанному). Следовательно, они пересекаются.

Следствие.

Общая хорда (AA₁) двух пересекающихся окружностей перпендикулярна к линии центров и делится ею пополам.

Теоремы.

1. Если две окружности имеют общую точку на линии их центров или на ее продолжении, то они касаются.

2. Обратно: если две окружности касаются, то общая их точка лежит на линии центров или на ее продолжении.

Признаки различных случаев относительного положения окружностей.

Пусть имеем две окружности с центрами O и O₁, радиусами R и R₁ и расстоянием между центрами d.

Эти окружности могут находиться в следующих 5-ти относительных положениях:

1. Окружности лежат одна вне другой, не касаясь. В этом случае, очевидно, d > R + R₁ .

2. Окружности имеют внешнее касание. Тогда d = R + R₁, так как точка касания лежит на линии центров O O₁.

3. Окружности пересекаются. Тогда d R + R₁, потому что в треугольнике OAO₁ сторона OO₁ меньше суммы, но больше разности двух других сторон.

4. Окружности имеют внутреннее касание. В этом случае в d = R — R₁, потому что точка касания лежит на продолжении линии OO₁.

5. Одна окружность лежит внутри другой, не касаясь. Тогда, очевидно,

d R + R₁, то окружности расположены одна вне другой, не касаясь.

2. Если d = R + R₁, то окружности касаются извне.

3. Если d R — R₁, то окружности пересекаются.

4. Если d = R — R₁, то окружности касаются изнутри.

5. Если d R Е R₁. Значит, все эти случаи исключаются. Остается один возможный, именно тот, который требовалось доказать. Таким образом, перечисленные признаки различных случаев относительно положения двух окружностей не только необходимы, но и достаточны.